Verstrengeling: grondslag van de kwantummechanica
 In de natuur is een kwantum de kleinste ondeelbare hoeveelheid van een grootheid als energie, impuls of massa. Hoeveelheid van een grootheid is een veelvoud van dat kwantum, een grootheid is dus gekwantiseerd. Elk deeltje heeft zijn eigen kwantumtoestand. Soms werken twee of meer deeltjes op elkaar in en gedragen zich als het ware als een tweeling of meerling, ze zijn zgn. verstrengeld en vormen samen een verstrengeld systeem. Wanneer een groep deeltjes alleen beschreven kan worden met de kwantumtoestand van het hele systeem en niet door individuele kwantumtoestanden, noemt men de deeltjes "verstrengeld", d.w.z. de deeltjes beïnvloeden elkaars toestand. Verandering aan het ene deeltje doet een ander deeltje veranderen, waarmee het verstrengeld is. Verandert de energie van een deeltje door botsen dan verandert ook de energie van andere deeltjes want de totale energie van het verstrengelde systeem is, wegens de wet van energiebehoud, constant.
In de natuur is een kwantum de kleinste ondeelbare hoeveelheid van een grootheid als energie, impuls of massa. Hoeveelheid van een grootheid is een veelvoud van dat kwantum, een grootheid is dus gekwantiseerd. Elk deeltje heeft zijn eigen kwantumtoestand. Soms werken twee of meer deeltjes op elkaar in en gedragen zich als het ware als een tweeling of meerling, ze zijn zgn. verstrengeld en vormen samen een verstrengeld systeem. Wanneer een groep deeltjes alleen beschreven kan worden met de kwantumtoestand van het hele systeem en niet door individuele kwantumtoestanden, noemt men de deeltjes "verstrengeld", d.w.z. de deeltjes beïnvloeden elkaars toestand. Verandering aan het ene deeltje doet een ander deeltje veranderen, waarmee het verstrengeld is. Verandert de energie van een deeltje door botsen dan verandert ook de energie van andere deeltjes want de totale energie van het verstrengelde systeem is, wegens de wet van energiebehoud, constant.
Inhoud
- Globaal overzicht van de mechanica van de micro- en de macrowereld
- Grootmeesters van de klassieke en kwantummechanica
- Het begrip kwantumtoestand
- De Schröderinger vergelijking
- Verstrengelde kwantum toestanden
- Hoe komen verstrengelde deeltjes tot stand?
- Veeldeeltjestheorie
- Nawoord
Globaal overzicht van de mechanica van de micro- en de macrowereld
| Macrowereld, zichtbare wereld | Microwereld, onzichtbare kwantumwereld |
|---|---|
| Continuïteit: Alle grootheden als kracht, snelheid, impuls en energie zijn trappeloos te veranderen. In feite geldt ook hier de kwantummechanica maar de invloed is onmeetbaar klein. | Kwantificering: alle hoeveelheden van grootheden als massa, energie en impulsmoment, zijn een veelvoud van een kwantum, dat is de kleinste hoeveelheid van een grootheid. |
| Wetten van Newton voor de mechanica en Maxwell's wetten voor het elektromagnetisme. | Wat de wetten van Newton en Maxwell zijn voor de klassieke macrowereld is de Schöderingervergelijking voor de kwantummechanica in de microwereld. |
| Definitieve toestand van de objecten wordt eenduidig vastgelegd door te meten. Het meetinstrument beïnvloedt niet de meting bij macroscopische lichamen. | Superpositie is een samenstelling van twee of meer gelijksoortige grootheden. Deze superpositie kan zich opsplitsen in twee of meer grootheden met lagere energie. De som van de lagere energieën is wegens de wet van energiebehoud gelijk aan de totale energie van de superpositie. Verstrengeling is de fysische relatie (wederzijdse beïnvloeding) tussen de uit de superpositie ontstane twee of meer kwantumtoestanden. Het tweede kwantummysterie is dat deze verstrengeling (onderlinge beïnvloeding) blijft bestaan ook als deze deeltjes zich duizend kilometers van elkaar verwijderen, alsof een signaal ze blijvend verbindt. |
| Determinisme houdt in dat als we alle invloedfactoren zouden kennen, wat in de praktijk onmogelijk is, dan zouden we de toekomst nauwkeurig kunnen voorspellen. | Toeval houdt in dat toekomstvoorspelling geschiedt in termen van waarschijnlijkheid, overeenkomstig het karakter van de kwantummechanica. |
Grootmeesters van de klassieke en kwantummechanica
Newton, Maxwell en Bolzmann behoren bij de klassieke wereld. Einstein rondt de klassieke mechanica af met zijn speciale en algemene relativiteitstheorie en brengt in de kwantummechanica zijn E=MC2 in en toont verder aan dat licht zich behalve als golf ook als deeltje kan gedragen (foto-elektrisch effect). Andere grootmeesters van de kwantummechanica zijn: Planck met de invoering van het begrip kwantum en het gekwantiseerd zijn van energie, Bohr met zijn eerste "stabiele" atoommodel, De Broglie met zijn idee dat materie zoals elektronen ook golfeigenschappen hebben, Heisenberg komt met de onbepaaldheidsrelatie en Schrödinger met de Schrödingergolfvergelijking. De fysische en filosofische grondslag van de kwantummechanica begrijpen we niet, omdat het niet voldoet aan de logica waaraan we gewend zijn. Klassieke mechanica,
Klassieke mechanica,K=M.a
Isaac Newton 1643-1727
 Elektromagnetische golven,
Elektromagnetische golven,Maxwell 1831-1879
 Statistische mechanica,
Statistische mechanica,Ludwig Bolzmann 1844-1906
 Begrip kwantum E=hf in 1900,
Begrip kwantum E=hf in 1900,Max Planck 1858-1947
 Foto-elektrisch effect 1905, E=MC2
Foto-elektrisch effect 1905, E=MC2Albert Einstein, 1879-1955
 Paul Dirac,
Paul Dirac,1902-1984
Voorspelt bestaan antimaterie
 Eerste atoommodel met stabiele elektronen banen,
Eerste atoommodel met stabiele elektronen banen,Niels Bohr 1885-1962
 Max Born 1882-1970, Interpretatie Schrödingervergelijking in termen van waarschijnlijkheid
Max Born 1882-1970, Interpretatie Schrödingervergelijking in termen van waarschijnlijkheid Werner Heisenberg,
Werner Heisenberg,1901-1976,
Onbepaaldheidsprincipe
 Schrödinger,
Schrödinger,1887-1961,
Schrödinger golfvergelijking,
 Louis de Broglie,
Louis de Broglie,1892-1987,
Materie golven 1925, λ=h/mv
Het begrip kwantumtoestand
De kwantummechanica is in het eerste kwart van de 20e eeuw tot stand gekomen door het werk van vooral Planck, Einstein, Bohr, De Broglie, Heisenberg, Schrödinger en Born. Het is een fundamentele beschrijving van de natuur. De klassieke mechanica van Newton in de macroscopische wereld komt voort uit de kwantummechanica. De kwantumtheorie gaat over kansberekening, uitsluiting van bepaalde toestanden (Pauli uitsluitingsprincipe) en verstrengeling van vooral subatomaire deeltjes en fotonen en geeft een beeld van de fysische realiteit die onder de klassieke mechanica ligt. De theorie van de kwantummechanica is in strijd met onze logica, het is voor mensen niet echt te begrijpen, omdat er geen analogie te vinden is in de macrowereld. Volgens insiders liegt een wetenschapper die beweert dat hij de kwantummechanica begrijpt. Omdat deeltjes en fotonen, die behandelt worden in de microwereld, geen deeltjes en golven zijn volgens de klassieke mechanica, noemt men ze ook wel kwantumtoestanden en laten in het midden wat ze precies zijn.Een subatomair deeltje zoals een elektron is geen vast deeltje zoals wij dat kennen. Het kan het best omschreven worden met: de toestand waarin het kwantumobject zich bevindt, oftewel de kwantumtoestand. Deze toestand heeft onder bepaalde omstandigheden de eigenschappen van een vast deeltje en onder andere omstandigheden de eigenschappen van een golf. In werkelijkheid is het geen deeltje en geen golf, zoals wij die kennen in de zichtbare macrowereld, maar bezit het bepaalde eigenschappen van een deeltje en een golf. Maar juist omdat het geen deeltje of golf is in de klassieke betekenis kunnen de mysterieuze kwantummechanische verschijnselen optreden.
De Schröderinger vergelijking
In de kwantummechanica wordt de natuur beschreven door een differentiaalvergelijking, de zgn. Schrödingervergelijking. Als men de vergelijking oplost weet men de kwantumtoestand van bijvoorbeeld een elektron, d.w.z. waar het zich bevindt, wat zijn energie is, zijn impuls, zijn spin, maar alles in termen van waarschijnlijkheid. De kwantummechanica beschrijft de onzichtbare microwereld, waar de wetten van Newton niet opgaan. De Schrödingervergelijking is in de onzichtbare microkosmos wat Newton's K=Ma is in onze zichtbare macrowereld. De experimentele bevestiging van de juistheid van schröderings vergelijking kwam van Davisson en Germer in 1927.Gepolariseerde fotonen
Fotonen kunnen in het elektrisch veld in verschillende richtingen ‘trillen’. Een polarisatiefilter laat licht door dat in zijn voorkeursrichting trilt, van licht dat trilt in een ander vlak komt minder door de spleet. Na een verticaal polarisatiefilter is er alleen verticaal gepolariseerd licht. Als dat op een horizontaal filter valt, komt er niets doorheen.De eeneiige tweeling
Het gedrag van twee verstrengelde fotonen wordt mathematisch beschreven door een gemeenschappelijke golffunctie. De kwantummechanische verstrengeling is niet met onze klassieke mechanica verklaarbaar en komt over als een wonder. Het verschijnsel lijkt op een van de verhalen waarin iemand van een eeneiige tweeling een pijnscheut voelt in Amsterdam op het moment dat zijn broer in de Alpen bij het skiën een been breekt.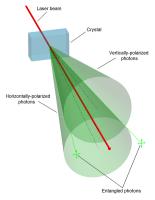 Spontane parametrische neerwaartse conversie proces fotonen kan splitsen in type II fotonparen met onderling loodrecht op elkaar staande polarisatie. / / Bron: J-Wiki, Wikimedia Commons (GFDL)
Spontane parametrische neerwaartse conversie proces fotonen kan splitsen in type II fotonparen met onderling loodrecht op elkaar staande polarisatie. / / Bron: J-Wiki, Wikimedia Commons (GFDL)De populaire methode voor het creëren van verstrengelde fotonen is gebruik van een BBO, dat is een dubbelbrekend barium-boraat kristal. De uittredende golffuncties overlappen elkaar door ze dicht bij elkaar te brengen. De breking levert twee bundels licht, waarvan de bovenste anders gepolariseerd is dan de onderste, maar wegens de behoudswetten is de totale verandering neutraal. Als we de toestand t.a.v. het polarisatievlak van het onderste foton weten, weten we op het zelfde moment de toestand (ligging polarisatievlak) van het andere foton.
Superpositie van opties
Het is de essentie van de natuur op kwantumniveau dat voor het meten van een toestand deze toestand een superpositie van mogelijkheden is. De soort meting bepaalt de kwantumtoestand (de toestand van het object), afhankelijk van de meting vindt men iets dat op een deeltje of op een golf lijkt. Let wel het is geen deeltje of golf uit de macrowereld maar laat zich wiskundig behandelen alsof het een deeltje of golf is.Wat gezegd wordt van één kwantumdeeltje geldt ook voor meerdere deeltjes. Na paarsgewijs genereren van twee of meer kwantumdeeltjes zijn deze verstrengeld. Tot de meting zijn ze een superpositie van potentiële toestanden. Als van twee verstrengelde deeltjes, bijvoorbeeld een elektron en een positron, het elektron verandert in een positron, dan verandert gelijkertijd het positron in een elektron, zodat de lading van het twee-deeltjes-systeem gelijk blijft. Ook als elektron en positron ver van elkaar verwijderd zijn beïnvloeden ze elkaar op deze manier. Het fascinerende van de verstrengeling is dat de verstrengelde deeltjes ruimtelijk gescheiden mogen zijn, de verstrengelde toestand blijft bestaan ook als de verwante deeltjes ver van elkaar verwijderd zijn. Werking op afstand is het moeilijkst te begrijpen deel van de kwantummechanica.
Verstrengelde kwantum toestanden
Twee of meer deeltjes worden verstrengeld genoemd als ze niet apart van elkaar zelfstandig kunnen worden omschreven. In de macrowereld is het normaal de eigenschappen van een object te beschrijven zonder de eigenschappen van andere objecten te kennen. Plaatsen en snelheid van een biljartbal na een botsing kan onafhankelijk van de andere ballen worden beschreven. In de kwantummechanica is dat niet altijd mogelijk.Verstrengeling van twee fotonen
Een standaard experiment voor het onderzoeken van het verschijnsel verstrengeling gaat uit van twee fotonen. Deze worden geproduceerd door een kristal dat de eigenschap heeft om uit een foton twee andere fotonen af te schieten. Vanwege behoudswetten, zoals het behoud van impuls, zijn de twee fotonen niet onafhankelijk. In het geval van polarisatie geldt dat als de polarisatie van de ene foton bekend is, dat ook het polarisatievlak van het andere foton bekend is, er hoeft maar één gemeten te worden.Hoe komen verstrengelde deeltjes tot stand?
Elke reactie waarbij twee deeltjes geproduceerd worden zorgen de behoudswetten ervoor dat de deeltjes verstrengeld zijn. De verstrengeling duurt totdat een van de deeltjes opnieuw een wisselwerking aangaat.- Hun golffuncties te laten overlappen, door ze dicht bij elkaar te brengen.
- Een elektron produceren, het positron krijgt men er ongevraagd bij.
- Als deeltjesparen gemaakt worden door het verval van andere deeltjes, natuurlijk of door een opgewekte botsing, dan mogen die deeltjesparen "verstrengeld" genoemd worden, zulke paren zijn gekoppeld en hebben tegenovergestelde eigenschappen, van spin of lading.
- De meest populaire methode (voor verstrengelde fotonen) maakt gebruik van een BBO: een barium-boraat kristal, dat dubbelbrekend is.
Veeldeeltjestheorie
Het is vaak noodzakelijk om de toestand van een kwantumobject te begrijpen dat vele deeltjes bevat. Dat zijn onder andere de atomen die meer dan één elektron bevatten, elk elektron heeft invloed op de andere elektronen in het atoom. Een belangrijke kwestie bij de vele deeltjessystemen zoals een atoom is of het mogelijk is om twee deeltjes te onderscheiden. Verschillende deeltjes gehoorzamen een fundamenteel andere wet dan gelijke deeltjes. Zo kunnen twee verschillende deeltjes gemakkelijk stoppen en verblijven op dezelfde plaats. Een verblijf van niet-onderscheidbare deeltjes is echter beperkt door het uitsluitingsprincipe van Pauli, dat zegt dat er geen twee elektronen in dezelfde elektronenbaan kunnen zitten die alle kwantumgetallen gelijk hebben, in dat geval moet de spin verschillend zijn.In de kwantumwereld, kunnen twee of meer deeltjes zodanig dicht bij elkaar zijn dat ze niet zelfstandig te beschrijven zijn. Deze deeltjes bevinden zich dan in een gemeenschappelijke verstrengelde toestand. Deeltjes (bijvoorbeeld elektronen en fotonen), worden beschreven met behulp van de Schrödinger vergelijking. Die bevat alle informatie over een systeem, zoals plaats, impuls, energie en spin.
Als men vraagt "waar het elektron is", krijgt men een kansverdeling te zien, die volgt uit de golffunctie. De verwachtingswaarde is de meest waarschijnlijke uitkomst. Bij een waterstofatoom is bijvoorbeeld de Bohr-straal de meest waarschijnlijke afstand waarop je het elektron van de kern zal aantreffen.
Nawoord
De verstrengeling (correlatie genoemd in de macrowereld) tussen deeltjes is noodzakelijk om het evenwicht in de schepping te behouden. Als uit een neutraal deeltje twee deeltjes ontstaan waarvan de een negatief is, is de ander positief om het evenwicht in stand te houden. Wat we ook doen, de twee deeltjes zullen tegengestelde ladingen hebben. Dit geldt ook voor de polarisatie van fotonen.De golffunctie van het universum, de scheppingsformule
Een manier om de fysica te interpreteren is om het hele universum als een enkele golffunctie te beschouwen. Deze "golffunctie van het universum" zou een term bevatten die de kwantumtoestand van elk deeltje definieert. Deze denkwijze opent deuren naar het idee dat in de schepping alles met elkaar verbonden is. De kwantumtoestand van elk deeltje in het heelal beïnvloedt de golffunctie van elk ander deeltje.Informatieoverdracht
Informatieoverdracht over afstand tegelijk met de toestandtransformatie is niet mogelijk, omdat informatie niet in een tijdloze transactie (instantaan) meegestuurd kan worden, maar maximaal met de lichtsnelheid. Dat kost tijd terwijl de transformaties tegelijkertijd plaatsvinden. Kwantumverstrengeling is het meest onbegrepen verschijnsel in de kwantummechanica. Als u het niet begrijpt ligt dat niet aan u en waarschijnlijk ook niet aan het artikel.Conclusies
- De kwantummechanica doet slechts statistische uitspraken over te verwachten resultaten.
- De elektronenbundels vertonen als lichtbundels diffractie-interferentie en brekingsverschijnselen.
- De spin is het kwantummechanische broertje van het impulsmoment uit de macrowereld.
- De kwantummechanica is ook van toepassing in de macrowereld onzichtbare microwereld beheerst de zichtbare macrowereld. de kwantummechanica
- De werkelijke massa van het universum bestaat uit ons bekende materie, maar 85% bestaat uit (zwarte) donkere materie, dat ook tot de microwereld behoort. Het is niet onwaarschijnlijk dat deze donkere materie het mysterie van de kwantumverstrengeling en in het bijzonder de werking op afstand zal oplossen.
- Het lijkt alsof het heelal, als deel van het universum dat uit één oerknal voortkomt, een geheel vormt waarin alles met elkaar verstrengeld is.
- De grote toekomst van de kwantumverstrengeling ligt in de computer- en communicatietechnologie.
Lees verder
© 2016 - 2024 Custor, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Heisenberg's onzekerheidsprincipeVeel natuurkundige wetten zijn vaak logisch en begrijpbaar. Dat is niet het geval met Heisenberg's onzekerheidsprincipe…
Heisenberg's onzekerheidsprincipeVeel natuurkundige wetten zijn vaak logisch en begrijpbaar. Dat is niet het geval met Heisenberg's onzekerheidsprincipe…
 Zwaartekrachtsgolven, wat zijn dat?Na een zoektocht van ongeveer 100 jaar zijn wetenschappers erin geslaagd om zwaartekrachtsgolven te detecteren. Op 11 fe…
Zwaartekrachtsgolven, wat zijn dat?Na een zoektocht van ongeveer 100 jaar zijn wetenschappers erin geslaagd om zwaartekrachtsgolven te detecteren. Op 11 fe…
 Snelheid: Rekenen met formulesSnelheid zie je overal op verkeersborden, maar ook in de computertaal, kb/sec. Maar snelheid is meer dan alleen dat, bij…
Snelheid: Rekenen met formulesSnelheid zie je overal op verkeersborden, maar ook in de computertaal, kb/sec. Maar snelheid is meer dan alleen dat, bij…
Gerelateerde artikelen
De kwantummechanica en esoterieDe kwantummechanica bestudeert de wijze waarop atomen zijn opgebouwd. Een atoom is geen vast deeltje, geen bolletje of p…
Fotonen voor dummiesLicht is een heel speciaal verschijnsel. We staan er in het dagelijks leven niet vaak bij stil, maar ook licht bestaat u…
KwantummechanicaIn het begin van de vorige (20e) eeuw hebben een aantal wetenschappers een nieuwe natuurkundige theorie ontwikkeld, die…
Bronnen en referenties
- Inleidingsfoto: Adrien Facélina, Wikimedia Commons (LGPL)
- http://rationalisingtheuniverse.org/2015/11/27/the-same-places-the-same-time-the-same-object/
- https://simple.wikipedia.org/wiki/Quantum_entanglement
- http://www.quantenwelt.de/quantenmechanik/vielteilchen/verschraenkung.html
- https://nl.wikipedia.org/wiki/Kwantumgetal
- http://www.focus.de/wissen/mensch/naturwissenschaften/quantenphysik-endlich-verstanden-deshalb-kann-ein-objekt-an-zwei-orten-gleichzeitig-sein_id_4352630.html
- Nl.wikipedia.org/wiki/Schr%C3%B6dingervergelijking...
- Wetenschapsforum.nl/index.php?showtopic=3731
- https://www.picoquant.com/applications/category/quantum-optics/quantum-entanglement (Afbeelding verstrengeling twee elektronen)
- http://www.kennislink.nl/publicaties/kwantumbeveiliging (afbeelding polarisatie)
- http://www.quantumuniverse.nl/quantumfysica-5-de-
- Schr%C3%B6dingervergelijking
- http://www.heise.de/tp/artikel/12/12934/1.html
- https://nl.wikipedia.org/wiki/Dubbele_breking
- https://nl.wikipedia.org/wiki/Kwantumverstrengeling
- http://www.timeone.ca/cast/type/physicists/page/2/#sthash.wrcbooqG.dpbs (foto Max Born)
- Afbeelding bron 1: J-Wiki, Wikimedia Commons (GFDL)
Custor (173 artikelen)
Laatste update: 04-02-2017
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 17
Laatste update: 04-02-2017
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 17
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.