Niet-euclidische meetkunde, een weerlegging van Kant?

De euclidische meetkunde kennen we allemaal, al kan het zijn dat je er nog nooit van gehoord hebt. Dit is namelijk de wiskunde die wij hebben geleerd op de middelbare school, en de enige manier van nadenken over ruimte die wij ons kunnen voorstellen. Maar nu is er ook een andere soort wiskunde, die niet-euclidische, die niet zo intuïtief is. En deze vormt een probleem voor Kant en zijn theorie, die namelijk gebaseerd is op een aanname die bewezen wordt door aan te nemen dat euclidische meetkunde de enige mogelijke soort wiskunde is.

Euclidische meetkunde

Een wiskundig systeem bestaat altijd uit een aantal axioma's, aannames, waarop de rest van het systeem gebaseerd is. De euclidische meetkunde is de wiskunde die begonnen is door de Griek Euclides, en deze bestaat uit de volgende axioma's, de postulaten van Euclides:

• Twee punten kunnen verbonden worden door een rechte lijn.
• Elke rechte lijn kan eindeloos als rechte lijn uitgebreid worden.
• Elk lijnstuk kan de straal zijn van een cirkel met een van de uiteinden van dat lijnstuk als middelpunt.
• Alle rechte hoeken zijn congruent.
• Door een punt buiten een oneindig lange rechte lijn gaat precies één oneindig lange lijn die de eerste niet snijdt.

Deze aannames zijn intuïtief erg aannemelijk. Natuurlijk kunnen twee punten worden verbonden door een rechte lijn en natuurlijk zijn alle rechte hoeken congruent. Het laatste postulaat houdt in dat parallelle lijnen elkaar niet kunnen raken. Ook dit lijkt logisch. Wij kunnen ons geen wereld voorstellen waarin dit niet het geval is. Maar is dit wel zo vanzelfsprekend?

Niet-euclidische meetkunde

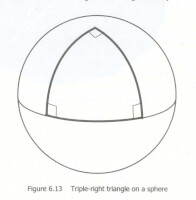
De niet-euclidische meetkunde trekt het laatste axioma in twijfel. Wat nu als we aannemen dat parallelle lijnen elkaar wel kunnen raken? Het is slechts een intuïtieve aanname, het idee is nergens door bewezen, we kunnen hem ook niet aannemen. Dan blijkt dat de wiskunde die hieruit volgt best goed werkt en logisch consistent is. Het zorgt ervoor dat de ruimte uit meer dan drie dimensies bestaat en dat driehoeken van meer dan 180 graden bestaan. Dit is niet voor te stellen voor mensen, maar dat betekent nog niet dat het onmogelijk is. De euclidische meetkunde is ook precies zo aannemelijk doordat het in een driedimensionale ruimte werkt, daardoor lijken de axioma's ervan zo vanzelfsprekend.

Synthetische oordelen a priori

Wat heeft dit nu met Kant te maken? Kant had de euclidische meetkunde nodig als enige vorm van wiskunde om te bewijzen dat synthetische oordelen a priori bestaan, een fundamenteel deel van zijn theorieën. Wat zijn synthetische oordelen a priori? Kant maakt twee soorten onderscheid in oordelen. Er bestaan a priori en a posteriori oordelen. A priori betekent 'voor de waarneming'. A priori oordelen bestaan dus uit kennis die we hebben zonder dat we hier bewijzen, bepaalde ervaringen of experimenten voor nodig hebben. A posteriori oordelen volgen juist uit de waarneming. Het andere onderscheid is dat tussen analytische en synthetische oordelen. Analytische oordelen zijn tautologieën. Een voorbeeld is 'een cirkel is rond'. Dit is altijd waar, maar geeft eigenlijk geen informatie over iets anders dan wat we bedoelen met cirkel, namelijk iets wat rond is. Met alleen analytische oordelen kunnen we geen nieuwe kennis verkrijgen. Synthetische oordelen bestaan juist uit combinaties van kennis, waardoor nieuwe kennis mogelijk is, bijvoorbeeld 'deze cirkel is rood'. Nu is het zo dat als synthetische oordelen a priori bestaan, dat deze oordelen geen ervaring of experimenten nodig hebben, maar toch nieuwe informatie kunnen geven. En dit zou betekenen dat er zonder experimenten nieuwe kennis kan worden gevonden, simpelweg met redeneren. Dit werd door veel filosofen onmogelijk geacht, maar Kant geloofde er wel in en probeerde deze te bewijzen.

Het bewijs van Kant

De axioma's van de meetkunde zijn a priori. Ze zijn intuïties, en we weten zeker dat ze waar zijn. Het is in onze voorstelling niet mogelijk dat parallelle lijnen elkaar raken, en daarom lijkt het niet te kunnen. En de wiskunde die hierop gebaseerd is, op axioma's, die a priori zijn, geeft ons nieuwe informatie. Deze informatie moet dan uit synthetische oordelen a priori bestaan, er zijn geen experimenten nodig voor de wiskunde. Je zou kunnen zeggen dat de wiskunde één grote tautologie is, maar dit is niet hoe Kant het zag. Hij dacht wel degelijk dat de wiskunde nieuwe informatie geeft.

Het probleem

Maar wat als ook niet-euclidische meetkunde mogelijk is? Nu lijken die a priori ideeën over ruimte en lijnen helemaal niet zo logisch te zijn. Het kon wel eens zijn dat onze intuïtie het mis heeft, waarom zou die het ook altijd bij het juiste eind hebben? Welke axioma's we gebruiken voor de wiskunde lijkt min of meer willekeurig, we hebben de keus uit intuïtief aannemelijke axioma's en niet aannemelijke, maar ze kunnen beide werken. Einstein heeft ook al aangetoond dat de ruimte helemaal niet euclidisch is, dus niet uit maar drie dimensies bestaat, maar uit meer. Dit lijkt ook een sterk bewijs voor het feit dat onze intuïties over ruimte niet te vertrouwen zijn. Kunnen we hier dan geen a priori oordelen over doen? Dat betekent dat die synthetische oordelen a priori misschien ook niet bestaan, of in elk geval niet op deze manier bewezen kunnen worden. En dit is juist wat Kant's systeem nodig heeft.

Het mogelijke antwoord van Kant

Nu heeft Kant het niet meer meegemaakt dat de wetenschap de kant van de niet-euclidische wiskunde op ging, en hij heeft dus niet de kans gehad dit probleem op te lossen. Maar er zijn wel manieren het probleem te verwerpen die bij zijn theorieën aansluiten. Je zou bijvoorbeeld kunnen zeggen dat synthetische oordelen a priori niet gaan over de 'dingen in zichzelf'. De dingen in zichzelf zijn volgens Kant, dat, wat werkelijk bestaat. Wij hebben een beeld van de werkelijkheid maar dit bestaat slechts uit de perceptie die onze zintuigen en ons brein ervan kunnen vormen, wij kunnen niets te weten komen over hoe de dingen echt zijn, over de dingen in zichzelf. En dit beeld dat wij van de werkelijkheid hebben is drie dimensionaal, dat de dingen in zichzelf uit veel meer dimensies zouden bestaan is mogelijk, maar dit is niet waar onze a priori oordelen over gaan. Die gaan juist over de wereld hoe wij die waarnemen, en ze bestaan dus binnen die wereld, die driedimensionale wereld, die euclidische ruimte. Sterker nog, wat wij hier ook over zeggen en berekenen, de ruimte zelf is slechts een creatie van ons brein, slechts de manier waarop wij de werkelijkheid ervaren. De dingen in zichzelf zijn helemaal niet ruimtelijk, het heeft dus geen zin om er dat soort uitspraken over te doen.

Oplossing

Bovenstaande beargumenteert waarom het niet relevant is dat de niet-euclidische meetkunde ook kan bestaan. Er zijn dus verschillende manieren om te denken over wat a priori oordelen zijn, en waar ze over oordelen, over de ruimte van de waarneming of over hoe 'het werkelijk in elkaar zit'. En bovenal, als we dit bewijs van synthetische oordelen a priori verwerpen, is het nog steeds mogelijk daar een ander bewijs voor te verzinnen, het tegenovergestelde is ermee nog niet bewezen. En als Kant nog had geleefd had hij dit misschien al wel gedaan.