Wanneer is een systeem chaotisch?
 Wanneer het principe dat vergelijkbare oorzaken leiden tot vergelijkbare effecten niet meer geldt, dan is er sprake van een chaotisch systeem. Twee eigenschappen bepalen - meestal - of een systeem chaotisch is of niet. Ten eerste moet er sprake zijn van een feedback-loop waarin de output weer als input gebruikt wordt. Ten tweede moet er een niet-lineair verband bestaan tussen input en output.
Wanneer het principe dat vergelijkbare oorzaken leiden tot vergelijkbare effecten niet meer geldt, dan is er sprake van een chaotisch systeem. Twee eigenschappen bepalen - meestal - of een systeem chaotisch is of niet. Ten eerste moet er sprake zijn van een feedback-loop waarin de output weer als input gebruikt wordt. Ten tweede moet er een niet-lineair verband bestaan tussen input en output.
Vergelijkbare oorzaken, onvergelijkbare gevolgen
De chaostheorie combineert determinisme met onvoorspelbaarheid. Wiskundig gezien heeft het determinisme de vorm van een functie die met dezelfde input altijd dezelfde output levert. Vrijwel alle bekende natuurwetten zijn deterministisch. Daarom zijn ze ook zo praktisch in het gebruik. Als de wetten of functies goed gekozen zijn dan zijn voorspellingen mogelijk. De nauwkeurigheid van de voorspellingen hangt af van de nauwkeurigheid waarmee de input gemeten is. De tweede wet van Newton - F = m a - is zo’n bruikbare wet. Wanneer de massa m en de versnelling a gegeven zijn, dan volgt uit de vergelijking de kracht F die het voorwerp op een ander voorwerp uitoefent. Als functie heeft F de twee inputs m en a en kan dus geschreven worden als F(m,a). Wanneer m en a dezelfde zijn, zal F(m,a) altijd dezelfde waarde opleveren. Maar als m en a niet nauwkeurig gemeten zijn dan zal ook de berekende kracht niet precies bepaald kunnen worden.Die onnauwkeurigheid is in de meeste gevallen niet zo erg. Men gaat er, meestal terecht, van uit dat kleine meetfouten geen grote gevolgen hebben. Als de ene keer de massa van een voorwerp als 1 kg gemeten worden en een volgende keer als 1 kg en een gram, dan heeft dat niet zoveel gevolgen voor de berekende kracht. Het determinisme - zelfde oorzaak, zelfde effect - wordt in de praktijk verzacht door het idee dat vergelijkbare oorzaken vergelijkbare effecten hebben. Bij chaotische systemen echter werkt dit milde determinisme niet meer. In de theorie van chaotische systemen kunnen vergelijkbare - maar niet identieke - oorzaken tot totaal verschillende effecten leiden. Ed Lorenz, een van de vaders van chaos-theorie, noemde dit het butterfly-effect; een enkele vleugelslag van een vlinder op een zomerse dag in een ver land kan hier een orkaan veroorzaken. De vleugelslag maakt maar een heel klein verschil, maar de effecten kunnen desondanks desastreus zijn.
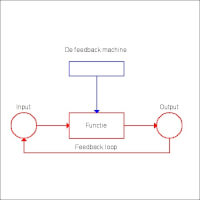 Figuur 1
Figuur 1De feedback machine
De hamvraag is natuurlijk wat het verschil is tussen de chaotische en de normale systemen zoals de tweede wet van Newton. Het antwoord heeft twee delen: feedback en non-lineariteit. Wat feedback is laat zich goed illustreren aan de hand van getalreeksen en iteratieve functies. Het principe van feedback is geschetst in figuur 1 (klikken maakt de figuur groter).Het gedeelte in rood is de eigenlijke feedback machine. Het heeft een input die door een processor - de functie - wordt omgezet in een output. In de volgende stap wordt de output verplaatst naar de input en wordt er een nieuwe output uitgerekend. Het gedeelte in blauw beschrijft de setup van de processor. De functie kan werken met parameters die vooraf ingesteld moeten worden en die tijdens het lopen van de machine onveranderd blijven. De tweede wet van Newton is duidelijk geen feedback machine. Er is - normaal gesproken - geen mogelijkheid om de berekende waarde van F weer als input in de vergelijking terug te stoppen. Input en output zijn hier van een te verschillende vorm.
Een getallenreeks die begint met een getal en een regel heeft om uit elk getal een volgend getal te berekenen, is wel een feedback machine. Laat bijvoorbeeld een reeks beginnen met het getal x(0) (de 0 duidt het tijdstip aan waarop de feedback machine begint te lopen) en laat de processor de functie x(i+1)=a x(i) uitvoeren, waarin i loopt van 0 tot mogelijk oneindig. Nu is er wel sprake van een feedback machine. Het uitgerekende getal kan immers weer als input voor de functie. De parameter a is de in te stellen parameter. Met x(0) = 1 en a = 2 kan de volgende reeks van getallen gemaakt worden:
- 1, 2, 4, 8, 16, 32, 64, 128,...
Functies waarvan de output weer als input gebruikt kunnen worden ook wel iteratieve functies genoemd. Zij vormen het wiskundig equivalent van de feedback machine.
Terzijde: meerdere inputs en meerdere outputs
Een getallenreeks wordt gevormd door een functie met een input en een output. Maar het is helemaal niet lastig dit te generaliseren naar functies met meer argumenten. Neem bijvoorbeeld de volgende twee gekoppelde functies- x(i+1) = y(i)
- y(i+1) = y(i) + x(i)
waarbij x(0)=y(0)=1.
Dit leidt in principe tot twee reeksen, een voor de x waarden en een voor de y waarden. Een beetje algebra leert dat y(n+1) = y(n) + y(n-1). Deze reeks - beter bekend als de Fibonacci reeks - laat zien dat door gebruik te maken van gekoppelde reeksen een reeks gemaakt kan worden waarin de huidige waarde afhangt van meerdere voorafgaande waarden.
Kortom: iteratieve functies kunnen in zeer veel situaties toegepast worden.
Non-lineariteit
Hoewel x(i+1) = a x(i) een voorbeeld van een feedback machine is, vertoont het nog geen chaotisch gedrag. Als x(0) een gemeten grootheid is, en dus meetfouten bevat, dan zullen kleine meetfouten er nauwelijks toe doen. Als x(0)=1 de “ware” waarde is en het wordt gemeten als x(0) = 1.01 dan leidt dat tot de volgende reeks: 1.01, 2.02, 4.04, 8.08, 16.16, .... De meetfout van 1% waarmee x(0) bepaald is, leidt uiteraard tot fouten in de reeks, maar die fouten nemen niet toe. In feit gaat het om een constante fout van 1% voor alle getallen in de reeks. De aanname dat vergelijkbare oorzaken tot vergelijkbare gevolgen leiden is hier gewoon geldig. Chaos ontbreekt in elk geval.Om echte chaotische systemen te krijgen is dus meer dan alleen maar feedback nodig. Non-lineariteit is het extra ingrediënt dat nodig is. Neem als regel dat x(i+1)=x(i)*x(i) + c. Dit is een niet-lineaire functie omdat het een kwadratische component heeft, namelijk x(i)*x(i). Deze functie zorgt wel degelijk voor chaotisch gedrag. Met x(0)=0.5 en c = -2 leidt dit tot de reeks getallen in de volgende tabel. Om het effect van meetfouten duidelijk te maken, staat in de tweede kolom de reeks die ontstaat wanneer x(0)= 0.505, dus wanneer er een meetfout is van 1% in de initiële waarde.
| Stap | x(0) | x(0) met fout | fout (%) |
|---|---|---|---|
| 0 | 0.5 | 0.505 | 1.0 |
| 1 | -1.75 | -1.744975 | 0.3 |
| 2 | 1.0625 | 1.044937750625 | 1.7 |
| 3 | -0.87109375 | -0.9081050973187654 | 4.2 |
| 4 | -1.241195678710938 | -1.175345132223676 | 5.3 |
| 5 | -0.4594332871492952 | -0.6185638201581105 | 34.6 |
| 6 | -1.788921054659193 | -1.617378800391405 | 9.6 |
| 7 | 1.20023853980296 | 0.6159141839555393 | 48.7 |
| 8 | -0.559427447571659 | -1.620649718002382 | 189.7 |
| 9 | -1.687040930903459 | 0.6265055084612001 | 62.9 |
| 10 | 0.8461071025436091 | -1.607490847867773 | 90.0 |
Dat dit een chaotisch systeem is, blijkt uit de kolom met de meetfouten. Al na een klein aantal stappen worden deze aanzienlijk en op stap 8 overschrijdt het zelfs (verre) een waarde van 100%. Dat wil zeggen dat de fouten van dezelfde orde zijn als de berekende waarden zelf. Het signaal (de ware waarden) verdrinkt als het ware in de ruis.
In deze tabel is gedaan alsof in de tweede kolom de ware waarden staan. Maar zelfs dat is een illusie. Elke computer rondt de getallen af en introduceert daarmee ergens in de reeks een fout. Deze analyse laat zien dat die fouten al heel snel de overhand krijgen zodat ook de waarden in de eerste kolom met een flinke korrel zou genomen worden. Het simuleren van chaotische systemen op een computer is daarom bijna onmogelijk. Het enige dat zinvol is, is gaan zoeken naar mathematische regelmatigheden. Zo kan bijvoorbeeld gelet worden op punten die onder de transformatie stabiel zijn, dus punten waarvoor geldt dat x = x*x +c. Verder kan gekeken worden naar welke punten naar oneindig gaan en welke niet. Dit type eigenschappen maken het onderzoek naar chaotische systemen boeiend.
Uiteraard hoeft het niet alleen maar om meetfouten te gaan. Met de voorbeelden is getoond onder welke omstandigheden hele kleine verschillen in input tot grote verschillen in output kunnen leiden. Dat is is de kern van een chaotisch systeem.
Slotwoord
Hier is weinig meer gedaan dan bepalen wanneer een systeem chaotisch verdrag vertoont. Er is een feedback machine nodig die middels een iteratieve functie gemodelleerd kan worden en die iteratieve functie moet non-lineair zijn. In zulke gevallen mag niet meer worden aangenomen dat vergelijkbare oorzaken vergelijkbare effecten als gevolg hebben en pas dan kan er sprake zijn van chaotisch gedrag.Er valt veel meer te zeggen over chaotische systemen. De niet-lineaire vergelijking die hier als voorbeeld gebruikt is - x(i+1) = x(i)*x(i) +c - is niet toevallig zo gekozen. Het vertegenwoordigt een omvangrijke klasse van chaotische systemen, waaronder de logistische vergelijking, en wordt ook veel gebruikt voor de constructie van fractals zoals de Mandelbrot verzameling. Er is ook een nauw verband tussen chaos en fractals. Hier hebben we ons echter beperkt tot een duiding van wat een chaotisch systeem eigenlijk is.
© 2015 - 2024 Henkellermann, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Het ontvangen van feedbackHet ontvangen van feedback is lastiger dan het lijkt; vaak kan feedback (gevraagde of ongevraagde feedback) emoties opro…
Het ontvangen van feedbackHet ontvangen van feedback is lastiger dan het lijkt; vaak kan feedback (gevraagde of ongevraagde feedback) emoties opro…
 Gespierd lichaam voor beginners!Tegenwoordig is de doelstelling van veel adolescenten: het gespierde lichaam ontwikkelen. Veel jongeren én volwassenen t…
Gespierd lichaam voor beginners!Tegenwoordig is de doelstelling van veel adolescenten: het gespierde lichaam ontwikkelen. Veel jongeren én volwassenen t…
 Het vragen van feedback; waarom, aan wie en hoe?Het vragen van feedback is een goede manier om eventuele twijfels over het eigen functioneren weg te nemen of om duideli…
Het vragen van feedback; waarom, aan wie en hoe?Het vragen van feedback is een goede manier om eventuele twijfels over het eigen functioneren weg te nemen of om duideli…
 De wet van Benford: een inleidingIn de meeste toepassingen van de statistiek gaat het om getallen die iets betekenen. Ze verwijzen naar de temperaturen i…
De wet van Benford: een inleidingIn de meeste toepassingen van de statistiek gaat het om getallen die iets betekenen. Ze verwijzen naar de temperaturen i…
 Russell's paradoxDe paradox van Russell laat zien dat de verzameling van verzamelingen die zichzelf niet als element hebben onmogelijk is…
Russell's paradoxDe paradox van Russell laat zien dat de verzameling van verzamelingen die zichzelf niet als element hebben onmogelijk is…
Gerelateerde artikelen
Feedback geven en ontvangenAls feedback op een goede manier gegeven en ontvangen wordt is het erg waardevol om in de toekomst beter met bepaalde si…
Bronnen en referenties
- Peitgen‚ H.-O.‚ Jürgens‚ H.‚(1990). Fraktale: Gezähmtes Chaos‚ Carl Friedrich von Siemens Stiftung‚ München.
Henkellermann (60 artikelen)
Laatste update: 19-09-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Laatste update: 19-09-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.