Wiskunde: snijpunten van twee functies bepalen
 Hoe bepaal je het snijpunt van twee wiskundige functies? Dit is een belangrijk vraagstuk in de wiskunde. Twee rechte lijnen hebben precies een snijpunt, behalve wanneer de lijnen evenwijdig zijn. Een rechte lijn en een parabool hebben twee, een, of nul snijpunten. Om de snijpunten te vinden moet een tweedegraads-vergelijking worden opgelost, hiervoor kun je als hulpmiddel de discriminant D uitrekenen.
Hoe bepaal je het snijpunt van twee wiskundige functies? Dit is een belangrijk vraagstuk in de wiskunde. Twee rechte lijnen hebben precies een snijpunt, behalve wanneer de lijnen evenwijdig zijn. Een rechte lijn en een parabool hebben twee, een, of nul snijpunten. Om de snijpunten te vinden moet een tweedegraads-vergelijking worden opgelost, hiervoor kun je als hulpmiddel de discriminant D uitrekenen.
 -fig 1-
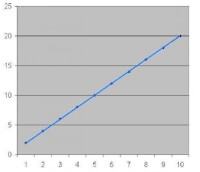
-fig 1-f(x) = 2x + 1
/ Bron: Tronic
Rechte lijnen
Voor het bepalen van het snijpunt van twee rechte lijnen bekijken we eerst de functie die een rechte lijn beschrijft. Een dergelijke functie ziet er als volgt uit:- f(x) = ax + b
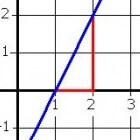
Men noemt dit ook wel een lineaire functie, zie figuur 1.
- f(x) = 2x + 1
deze lijn snijdt de x-as in het punt P(-1/2,0) en de y-as in het punt Q(0,1). De functie kan ook als de y-coördinaat worden geschreven:
- y = 2x + 1
 - fig 2-
- fig 2-(klik voor vergroting)
/ Bron: Tronic
Snijpunt van twee rechte lijnen
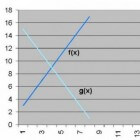
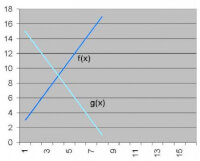
Om het snijpunt van de rechte lijnen te bepalen bekijken we de grafiek waarin deze twee lijnen zijn afgebeeld.- f(x) = 2x + 1
- g(x) = 17 - 2x
Deze functies zullen elkaar snijden in precies één punt: het snijpunt. Waar bevindt zich dit punt? Om het antwoord op deze vraag te vinden kunnen we stellen:
+ de coördinaten van het snijpunt S voldoen aan de functie f(x) en aan de functie g(x).
+ de y-coördinaat van snijpunt S voldoet aan zowel y = f(x) als y = g(x)
+ oftewel f(x) = g(x)
Om het snijpunt te vinden moeten we dus de volgende vergelijking oplossen:
- 2x + 1 = 17 - 2x
Oplossen levert: 4x = 16. Of: x = 16/4 = 4. De waarde x=4 invullen levert y=2*4+1=9. Het punt S(4,9) is het snijpunt van de twee functie's. Twee rechte lijnen hebben altijd precies één snijpunt, behalve wanneer de lijnen evenwijdig aan elkaar zijn.
Snijpunten van een rechte lijn en een parabool
grafisch
We bekijken nu hetzelfde vraagstuk, maar dan voor een parabool en rechte lijn. Gegeven de functie's: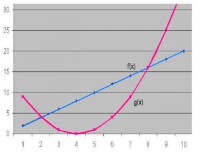 - fig 3 -
- fig 3 -2 snijpunten rechte lijn en parabool
/ Bron: Tronic
- f(x) = 2x
- g(x) = (x - 4)²
Waar bevindt zich het snijpunt van de twee functie's(?), en,
zijn er meer snijpunten denkbaar?
Zie figuur 3, op het eerste gezicht twee snijpunten; welke punten zijn dat? We passen weer het gelijkstellen van de functie's toe: f(x) = g(x) : 2x = (x - 4)².
Oplossen levert:
2x = (x - 4)² ↔
x² -10x + 16 = 0,
..via de abc-formule vinden we x=2 of x=8 (twee snijpunten). De snijpunten zijn: S1(2,4) en S2(8,16).
[...is de helling van de lijn nul (= 0), dan krijgen we 1 snijpunt S(4,0),
...en als de helling van de lijn (< 0),dan levert dat 0 snijpunten.]
abc formule
Een standaardvorm van een tweedegraadsvergelijking is:- ax² + bx + c = 0
De functie ax² + bx + c stelt een parabool voor. Gelijkstellen aan nul (= 0) levert:
x1,2 = (-b ± √ D) / 2a
D = b²- 4ac = de discriminant
het aantal oplossingen wordt zo bepaald:
- (D>0) -- de vergelijking heeft 2 oplossingen (x1 en x2)
- (D=0) -- één oplossing voor x
- (D<0) -- geen oplossing.
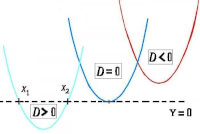 - fig 4- / Bron: Tronic
- fig 4- / Bron: TronicDe vergelijking ax² + bx + c = 0 stelt voor:
hoeveel snijpunten heeft de parabool (ax² + bx + c) met lijn (y = 0)?
(D < 0) is een speciaal geval. In onze gebruikelijke getallenverzameling R -rationele en irrationele getallen- heeft de vergelijking geen oplossing. Wordt R uitgebreid met complexe getallen (C), dan zijn er wel oplossingen mogelijk.
© 2010 - 2024 Tronic, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Het gebruik van het menu ‘CALC’ op de TI-84De rekenmachine genaamd TI-84 is een veelgebruikt hulpmiddel bij Wiskunde, Scheikunde, Economie- en Natuurkundelessen op…
Het gebruik van het menu ‘CALC’ op de TI-84De rekenmachine genaamd TI-84 is een veelgebruikt hulpmiddel bij Wiskunde, Scheikunde, Economie- en Natuurkundelessen op…
 Oplossen van polynomen - theorie en voorbeeldenIn veel beroepen wordt er gekeken naar polynomen. Wiskundigen stellen deze polynomen op om autoweggebruik in kaart te br…
Oplossen van polynomen - theorie en voorbeeldenIn veel beroepen wordt er gekeken naar polynomen. Wiskundigen stellen deze polynomen op om autoweggebruik in kaart te br…
 De richtingscoëfficiëntEen belangrijk wiskundig basisprincipe, dat een grote rol speelt bij het werken met functies en grafieken, is de richtin…
De richtingscoëfficiëntEen belangrijk wiskundig basisprincipe, dat een grote rol speelt bij het werken met functies en grafieken, is de richtin…
Gerelateerde artikelen
Kwadratische vergelijkingen oplossenEr zijn vier verschillende kwadratische vergelijkingen op te lossen. Het is daarom altijd belangrijk om eerst te kijken…
Hoe bereken je machtsfuncties?Wat zijn machtfuncties? Machtfuncties zijn functies in de wiskunde die bekend worden geacht voor het centraal eindexamen…
Priemgetallen begrijpenPriemgetallen zijn waarschijnlijk de meest bekende getallen binnen de wiskunde, en dan met name getaltheorie. Maar wat z…
Bronnen en referenties
- Inleidingsfoto: tronic
- Afbeelding bron 1: Tronic
- Afbeelding bron 2: Tronic
- Afbeelding bron 3: Tronic
- Afbeelding bron 4: Tronic
Tronic (33 artikelen)
Laatste update: 25-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Laatste update: 25-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.