De richtingscoëfficiënt
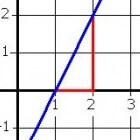 Een belangrijk wiskundig basisprincipe, dat een grote rol speelt bij het werken met functies en grafieken, is de richtingscoëfficiënt. Dit is een eigenschap van een rechte lijn, weergegeven door een getal. Deze coëfficiënt is een maat voor de steilheid van de lijn. Met behulp van de rico kan uit de grafiek van een lijn op simpele wijze de formule worden afgeleid, en vice versa.
De richtingscoëfficiënt, ook wel afgekort tot rico of rc, is een getal behorend bij een rechte lijn (of lijnstuk) in een twee-dimensionaal assenstelsel. De rico is een maat voor de steilheid van de lijn.
Een belangrijk wiskundig basisprincipe, dat een grote rol speelt bij het werken met functies en grafieken, is de richtingscoëfficiënt. Dit is een eigenschap van een rechte lijn, weergegeven door een getal. Deze coëfficiënt is een maat voor de steilheid van de lijn. Met behulp van de rico kan uit de grafiek van een lijn op simpele wijze de formule worden afgeleid, en vice versa.
De richtingscoëfficiënt, ook wel afgekort tot rico of rc, is een getal behorend bij een rechte lijn (of lijnstuk) in een twee-dimensionaal assenstelsel. De rico is een maat voor de steilheid van de lijn.Rico in de grafiek
De eenvoudigste manier om het concept van de rico te begrijpen, is door een rechte lijn in een x,y-assenstelsel te bekijken. Laten we voor het gemak eerst uitgaan van een stijgende lijn, dus een rechte die ‘van linksonder naar rechtsboven’ loopt.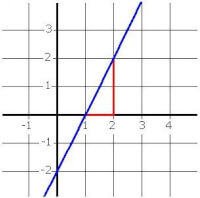
In de grafiek is dit te zien: wanneer de lijn één hokje naar rechts gaat (als de x-waarde met 1 toeneemt), gaat hij twee vakjes omhoog (neemt de y-waarde met 2 toe). De richtingscoëfficiënt is dus 2.
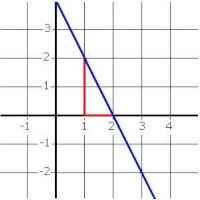
Een stijgende lijn heeft dus een positieve richtingscoëfficiënt, een dalende lijn een negatieve.
Voor de richtingscoëfficiënt wordt soms de notatie dy/dx of Δy/Δx gebruikt. Hierbij betekent dy of Δy de toename in de y-richting, in onze voorbeelden hierboven was dat eerst 2 en daarna -2 (het minteken staat er omdat er in het tweede geval een afname was). Om de rico te krijgen worden deze getallen gedeeld door dx of Δx, dit is de toename in de x-richting. Bij ons was dat steeds 1, zodat we die deling niet meer hoefden uit te voeren (delen door 1 geeft hetzelfde getal terug).
De rico kan zo op een algemenere manier gevonden worden, want de x-toename hoeft geen 1 te zijn. In ons eerste voorbeeld hadden we ook kunnen kijken wat er gebeurt als de x met 3 toeneemt. In dat geval neemt de y met 6 toe. We hebben dus dy = 6 en dx = 3, wat inderdaad de juiste richtingscoëfficiënt geeft: dy/dx = 6/3 = 2. In ons tweede voorbeeld zouden we bij dx = 3 gevonden hebben dat dy = -6: negatief want het is een afname. De rico wordt dus dy/dx = -6/3 = -2.
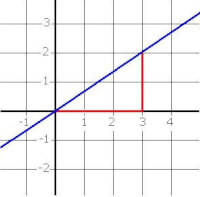
Dan zijn er nog twee speciale gevallen. Het eerste levert weinig problemen op: bij de horizontale lijn kunnen we gewoon de bovenstaande procedure toepassen. We komen dan natuurlijk tot de conclusie dat de rechte niet stijgt of daalt. Met andere woorden: als de x-waarde met 1 toeneemt, neemt de y-waarde met 0 toe (of af). De richtingscoëfficiënt van de horizontale lijn is dus 0.
Bij de verticale lijn loopt de boel echter wel in de soep. Bij deze rechte neemt de x-waarde immers nooit toe of af. De verticale lijn heeft dus geen rico – tenzij je wil zeggen dat de richtingscoëfficiënt oneindig is, wat prima is, maar waar je ook geen steek verder mee komt, aangezien oneindig geen getal is.
Rico in de formule
Een rechte lijn heeft een formule van de vorm y = ax + b, waarbij a en b vaste getallen zijn. Om precies te zijn is de a in deze formule de richtingscoëfficiënt. Dat dit overeenstemt met de interpretatie van de rico die we hierboven gezien hebben, is in te zien met een voorbeeld. Neem als a = 5 (dit is dus de rico) en b = 2, dus de formule is y = 5x + 2.Dit geeft de volgende tabel:
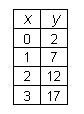
waarin duidelijk te zien is, dat elke keer dat de x-waarde met 1 toeneemt, de y-waarde met 5 toeneemt.
Overigens is met dit voorbeeld ook te zien wat de b in de formule is: dit is de y die hoort bij x = 0, oftewel: de y-coördinaat van het snijpunt van de lijn met de y-as.
Een horizontale lijn heeft als formule y = b. De x komt niet in de formule voor, omdat het niet uitmaakt welke x-waarde je in de formule stopt, de y-waarde is altijd dezelfde. In de formule is dus a = 0, wat klopt; de rico van een horizontale lijn was inderdaad 0.
Een verticale lijn heeft geen rico, wat betekent dat er geen formule te maken is, want we kunnen niets invullen voor a. Dat klopt: een verticale lijn heeft maar één x-waarde, waar alle y-waarden bijhoren. Maar je kunt alleen een formule maken als er bij een x maximaal één y hoort.
Conclusie
Door het kijken van de grafiek van een rechte lijn kun je de a en b uit de formule vinden. Met dy/dx (oftewel met ‘hokjes tellen’) vind je de richtingscoëfficiënt, oftewel het getal a, en uit het snijpunt met de y-as leid je de b af. Maar het werkt natuurlijk ook de andere kant op. Met deze kennis kun je nu ook de grafiek van een rechte tekenen als je de formule weet, zonder dat hiervoor nog een tabel gemaakt hoeft te worden. Begin dan met de b, waarmee je weet waar de lijn door de y-as gaat. Met behulp van de a kan de grafiek afgemaakt worden, omdat dit getal zegt hoe steil de lijn precies is.© 2011 - 2024 Mathmaarten, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
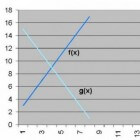 Wiskunde: snijpunten van twee functies bepalenHoe bepaal je het snijpunt van twee wiskundige functies? Dit is een belangrijk vraagstuk in de wiskunde. Twee rechte lij…
Wiskunde: snijpunten van twee functies bepalenHoe bepaal je het snijpunt van twee wiskundige functies? Dit is een belangrijk vraagstuk in de wiskunde. Twee rechte lij…
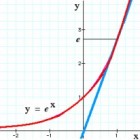 Wiskunde functieonderzoekFunctieonderzoek is een onderdeel van wiskunde dat beheerst moet worden in de bovenbouw. In dit artikel bekijken we acht…
Wiskunde functieonderzoekFunctieonderzoek is een onderdeel van wiskunde dat beheerst moet worden in de bovenbouw. In dit artikel bekijken we acht…
 Wiskunde - de afgeleide en extreme waardesHoe bereken je de extreme waardes, ook wel minimum en maximum, en hoe stel je een raaklijn op? Vaak wordt dit gezien als…
Wiskunde - de afgeleide en extreme waardesHoe bereken je de extreme waardes, ook wel minimum en maximum, en hoe stel je een raaklijn op? Vaak wordt dit gezien als…
 De booglengte van een kromme bepalen met PythagorasVoor een kromme lijn valt uit een formule lastig op te maken hoe lang bepaalde lijndelen zijn. Om dat te kunnen bepalen…
De booglengte van een kromme bepalen met PythagorasVoor een kromme lijn valt uit een formule lastig op te maken hoe lang bepaalde lijndelen zijn. Om dat te kunnen bepalen…
Gerelateerde artikelen
Bewijs dat 1 = 2Misschien wel de meest onomstotelijke, rotsvaste waarheid in de wiskunde, of zelfs in het leven in het algemeen, is dat…
Tafels van vermenigvuldiging in een handig overzichtEen handig hulpje om te vermenigvuldigen zijn de tafels, ook wel tafels van vermenigvuldiging genoemd. Kinderen leren de…
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.