De regel van Bayes en de medische diagnostiek
 De regel van Bayes gaat over de relatie tussen voorwaardelijke kansen. Het geeft een verband aan tussen kansen die niet altijd met onze intuïtie overeenkomt maar des te beter met de feiten. Niet goed omgaan met kansen kan tot desastreuze gevolgen leiden. De medische diagnostiek leert dat als geen andere discipline. De juiste toepassing van de regel van Bayes kan hier veel schade voorkomen. Aan de hand van een fictief voorbeeld uit de medische diagnostiek wordt de regel van Bayes afgeleid, uitgelegd, en het belang ervan aangetoond.
De regel van Bayes gaat over de relatie tussen voorwaardelijke kansen. Het geeft een verband aan tussen kansen die niet altijd met onze intuïtie overeenkomt maar des te beter met de feiten. Niet goed omgaan met kansen kan tot desastreuze gevolgen leiden. De medische diagnostiek leert dat als geen andere discipline. De juiste toepassing van de regel van Bayes kan hier veel schade voorkomen. Aan de hand van een fictief voorbeeld uit de medische diagnostiek wordt de regel van Bayes afgeleid, uitgelegd, en het belang ervan aangetoond.
Betrouwbare test en toch een slechte diagnose
Stel dat er een dodelijke ziekte is met de naam Z die bij 1 op de 1000 mensen voorkomt. Een man vreest dat hij Z heeft en wil daarop getest worden. Zou hij de ziekte hebben, dan volgt een medicijnbehandeling met nare neveneffecten. Gelukkig blijkt er een goede test beschikbaar te zijn voor deze ziekte. Als iemand Z heeft dan is de test zelfs voor 100% betrouwbaar. Iedereen die daadwerkelijk de ziekte heeft wordt dus altijd positief getest. Daar staat tegenover dat de test ook bij 5% van de gezonde mensen een positieve uitslag geeft. De hamvraag is deze: wat is de kans dat bij een positief test resultaat de man ook daadwerkelijk de ziekte Z heeft?Deze vraag is voorgelegd aan medicijnenstudenten van de elite universiteit te Harvard. Ongeveer de helft gaf 95% als antwoord. Bij een positief test resultaat is er volgens de overgrote meerderheid van hen een kans van 95% dat de man de ziekte Z daadwerkelijk heeft. De rest schatte het succespercentage lager in. Het gemiddelde van alle gegeven antwoorden kwam uit rond de 56%. Maar ook dat is een ernstige overschatting van de waren kans. De meeste studenten - en wellicht u ook - waren stomverbaasd toen ze het correcte antwoord vernamen. Er is slechts een kans van iets minder dan 2% dat de man echt ziek is.
De verklaring hiervoor moet gezocht worden bij de gezonde mensen die een kans van 5% hebben om toch als ziek getest te worden. In een populatie van 1000 mensen is er, als gezegd, slechts 1 die de ziekte heeft en ook als zodanig herkend wordt. Van de overige 999 wordt nog eens 5% positief getest. Een simpel rekensommetje leert dat in elke groep van 1000 mensen er 1 + 49,95 = 50,95 een positief test resultaat krijgen. Slechts een daarvan is echt ziek, dat is iets minder dan 2%.
De kwaliteit van een test hangt af van de verspreiding van de ziekte
Een goede test is dus nog wat anders dan een goede diagnose. De gevolgen van een slechte diagnose kunnen zeer ernstig zijn. Als de ziekte bij iemand aanwezig is met een kans van 95% dan is het meer dan redelijk de zware medicijnbehandeling door te voeren. Bij een kans van 2% ligt zo'n behandeling, zeker wanneer er veel nare neveneffecten zijn, echter helemaal niet voor de hand. De hoogte van de kans is natuurlijk van doorslaggevende betekenis bij de keuze voor een behandeling. Bij de keuze tussen leven en dood blijkt de statistiek toch een zeer bruikbare partner te zijn. Intuïtie en kansberekening lopen in dit geval zo ver uiteen dat het risico op een verkeerde behandeling levensgroot is.Dit voorbeeld maakt duidelijk dat het bij de interpretatie van een diagnose niet voldoende is om alleen op de kwaliteit van de test te letten. Het aantal "false alarms", dus het aantal keren dat de test positief uitslaat bij mensen die de ziekte niet hebben, speelt ook een grote rol, evenals de frequentie waarmee de ziekte in een populatie voorkomt. Het is niet alleen de test, maar ook de verspreiding van de ziekte die bepaalt of een diagnose verantwoord is of niet. Maar toch is de allerbelangrijkste conclusie dat een systematisch doorrekenen van de kansen tot radicaal andere conclusies kan leiden dan de schattingen op basis van intuïtie of gezond verstand doen. Het is al veel langer bekend dat mensen van nature slecht met toeval en kansen omgaan (zie bijvoorbeeld De miskenning van het toeval). Zeker in het geval van medische diagnoses kan dat ernstige gevolgen hebben. Ernstig, en volstrekt nodeloos. De statistiek is er wel degelijk en kan eenvoudig gebruikt worden.
De regel van Bayes
De redenering die tot de correcte conclusie van 2% kans leidde dat de man de ziekte Z had, kan in een algemene formule gegoten worden. Die formule is de regel van Bayes. Deze formule is niet alleen praktisch in het gebruik, maar maakt het ook mogelijk om de variabelen die de betrouwbaarheid van diagnoses beïnvloeden expliciet te benoemen en te bestuderen. Dit leidt niet alleen tot een beter inzicht in het diagnostisch proces zelf, maar uiteindelijk zelfs tot verantwoorde eisen voor medische tests. figuur 1
figuur 1Een goede manier om kansen te visualiseren is met behulp van Venn-diagrammen. In figuur 1 staat een voorbeeld. Het omringende vierkant stelt de hele populatie voor. In het voorbeeld is dat de verzameling van alle mensen. Binnen in het vierkant staat een cirkel afgebeeld die de kans op een gebeurtenis aangeven. In het voorbeeld zou dit kunnen staan voor alle mensen met de ziekte Z. De oppervlakte van de cirkel duidt de grootte van de kans aan. Als we het voorbeeld zouden volgen dan wordt de cirkel heel klein en vrijwel onzichtbaar en daarom is hier een (veel) te grote cirkel getekend. Het kan uitgerekend worden dat de kans die deze cirkel representeert gelijk is aan π/4 (Hint: de oppervlakte van een cirkel is gelijk aan π r² met r de straal. De straal is hier gelijk aan 1/2).
 figuur 2
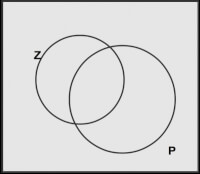
figuur 2- p(Z|P) = p(Z en P)/p(P)
Precies dezelfde redenering kan ook gevolgd worden voor de voorwaardelijke kans p(P|Z). In volstrekte analogie met het voorgaande volgt
- p(P|Z )= p(Z en P)/p(Z)
In beide formules komt de grootheid p(Z en P) voor zodat hieruit direct volgt
- p(Z|P) = p(P|Z)p(Z)/p(P)
Dit is de regel van Bayes. Het is dus geen regel die zomaar verzonnen is, ze volgt rechtstreeks uit de definities van kansen. In die zin is het vergelijkbaar met de regel 1+1=2. De regel is onontkoombaar.
Interpretatie van de regel van Bayes
Het is gebruikelijk, en handig, om de verschillende termen in deze regel een naam te geven. Allereerst de eenvoudige kansen p(Z) en p(P). Dit worden a priori kansen genoemd en geven in ons voorbeeld aan hoevaak in een bepaalde populatie de ziekte voorkomt - p(Z)- en hoevaak een test een positief resultaat geeft - p(P). De priori kans p(P) is soms gegeven en moet soms berekend of geschat worden.In ons voorbeeld is het niet direct gegeven. Wel is bekend dat de test 100% betrouwbaar is en dat het bij 5% van de mensen zonder de ziekte Z een positief resultaat geeft. Dit leidt direct tot p(P) = p(Z) + 0.05(1-P(Z)), waarin 1 - p(Z) de kans is dat een persoon niet ziek is. In het voorbeeld is p(Z) = 0.001 en dus is 1 - p(Z) = 0.999, waaruit we p(P) kunnen berekenen: p(P)=0,001 + 0,05 x 0.999 = 0,05095. Dat betekent dat in een populatie van 1000 mensen er 50,95 een positieve uitslag krijgen.
De voorwaardelijke kans p(P|Z) is de kans op een positief test resultaat gegeven dat de ziekte aanwezig is. Dit worden ook wel de "hits" genoemd. Het is een gedeeltelijke maat voor de betrouwbaarheid van de test. In het voorbeeld is deze gelijk aan 1. Deze voorwaardelijke kans wordt meer in het algemeen de "likelihood" functie van P gegeven Z genoemd. De ander voorwaardelijke kans, p(Z|P), dus de kans waar het uiteindelijk om gaat in voorbeelden als deze wordt de posteriori kans genoemd. Omdat de waarde van alle andere variabelen bekend is kan deze ook voor dit voorbeeld worden uitgerekend.
- p(Z|P) = p(P|Z)p(Z)/p(P) = 1 x 0.001/0,0505 = 1,96
Precies het antwoord dat al eerder gegeven was.
Wanneer is een diagnose wel betrouwbaar
Wat niemand wil is een betrouwbare test die tot verkeerde diagnoses leidt. Een minimale eis is dat het aantal mensen dat een correcte diagnose krijgt minstens even groot moet zijn als het aantal mensen dat een foute diagnose krijgt. Met behulp van de regel van Bayes wordt een goed inzicht verkregen in wat deze eis precies betekent.De kans op een correcte diagnose bij ziek mensen is uiteraard gelijk aan p(P|Z)p(Z). De kans op een incorrecte diagnose is gelijk aan p(P|G)p(G), waarin G de gezonde mensen aanduidt. De eis dat er meer correcte dan incorrecte diagnoses moeten zijn vertaalt zich dus in
- p(P|Z)p(Z)/p(P|G)p(G) > 1
oftewel
- p(P|Z)/p(P|G) > p(G)/p(Z)
Hier staat dat de verhouding tussen de kans op hits en de kans op false alarms groter moet zijn dan de kans op een gezond mens gedeeld door de kans op een ziek mens. Bij zeldzame ziektes zal p(G)/p(Z) zeer groot zijn en moet de verhouding tussen hits en false alarms dus ook zeer groot zijn.
Omgekeerd, wanneer de verhouding van hits en false alarms bekend is, dan kan uitgerekend worden hoe zeldzaam de ziekte mag zijn, wil de diagnose nog enigszins betrouwbaar zijn. In het voorbeeld was deze verhouding gelijk aan 1/0,05 = 20. Dus mag het aantal gezonde mensen slechts 20 maal groter zijn dan het aantal zieken om nog een goede diagnose te kunnen stellen. Aan die eis was in het voorbeeld duidelijk niet voldaan.
Slotwoord
De Bayes regel is hier afgeleid en uitgelegd en het belang ervan voor de medische diagnostiek is aangetoond. Zonder toepassing van de regel van Bayes is er een grote kans dat foute diagnoses worden gesteld. Ook is besproken welke eisen er aan een medische test, in termen van hits en false alarms, gesteld moeten worden wil de diagnose voor een ziekte met een gegeven frequentie van voorkomen nog enigszins acceptabel zijn.Lees verder
© 2015 - 2024 Henkellermann, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Liesklachten - differentiaal diagnostiekDoor het complexe gebied van anatomische structuren is het vaststellen van de diagnose bij liespijn een gecompliceerde f…
Liesklachten - differentiaal diagnostiekDoor het complexe gebied van anatomische structuren is het vaststellen van de diagnose bij liespijn een gecompliceerde f…
 Agressieve hiv-variant ontdekt in Cuba: na 3 jaar aidsWetenschappers hebben in 2015 een zeer agressieve vorm van hiv in Cuba ontdekt. Iemand die besmet is met dit virus, krij…
Agressieve hiv-variant ontdekt in Cuba: na 3 jaar aidsWetenschappers hebben in 2015 een zeer agressieve vorm van hiv in Cuba ontdekt. Iemand die besmet is met dit virus, krij…
Gerelateerde artikelen
mijn kijk opRisico en preventieAan preventieonderzoeken worden jaarlijks tientallen zo niet honderden miljoenen uitgegeven. Dit om het risico op ziekte…
Formules in de psychologische en pedagogische diagnostiekEr zijn verschillende standpunten tegenover de vraag of formules nut hebben in de psychologische en pedagogische diagnos…
Het Milgram experiment, gehoorzaamheid van de mensHet legendarische Milgram onderzoek werd in 1961 uitgevoerd door wetenschappelijk onderzoeker Stanley Milgram. Met dit o…
Bronnen en referenties
- Meehl, P.E., Rosen, P.A. (1955). Antecedent probability and the efficiency of psychometric signs, patterns, or cutting scores. Psychological Bulletin, May;52(3):194-216.
Henkellermann (60 artikelen)
Laatste update: 20-10-2016
Rubriek: Wetenschap
Subrubriek: Onderzoek
Bronnen en referenties: 1
Laatste update: 20-10-2016
Rubriek: Wetenschap
Subrubriek: Onderzoek
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.