Foutenanalyse: een must bij elk wetenschappelijk onderzoek
 Een meting van een grootheid zoals een massa, een lengte, een temperatuur, … resulteert in een meetresultaat gevolgd door een eenheid. Maar kun je zeker zijn van dit meetresultaat? Geeft dit resultaat de accurate waarde weer? Het antwoord is steeds nee. Hoe nauwkeurig je meettoestel ook werkt en hoe precies jij de meting ook uitvoert, er zal telkens een fout op je meetresultaat zitten. Deze fout is de kleinste waarde die het meettoestel kan meten. Om de waarde van een wetenschappelijk onderzoek te kunnen inschatten, is een foutenanalyse van de meetresultaten dus erg belangrijk.
Een meting van een grootheid zoals een massa, een lengte, een temperatuur, … resulteert in een meetresultaat gevolgd door een eenheid. Maar kun je zeker zijn van dit meetresultaat? Geeft dit resultaat de accurate waarde weer? Het antwoord is steeds nee. Hoe nauwkeurig je meettoestel ook werkt en hoe precies jij de meting ook uitvoert, er zal telkens een fout op je meetresultaat zitten. Deze fout is de kleinste waarde die het meettoestel kan meten. Om de waarde van een wetenschappelijk onderzoek te kunnen inschatten, is een foutenanalyse van de meetresultaten dus erg belangrijk.
- Soorten fouten
- Absolute fout (AF)
- Relatieve fout (RF)
- Procentuele fout (PF)
- Foutenanalyse bij berekeningen
- De absolute fout van een som/verschil
- De relatieve fout (procentuele fout) van een product/quotiënt
- De relatieve fout van een macht
- Voorbeeld van een wetenschappelijk onderzoek: bepaling van de dichtheid van een vloeistof
- Grafische weergave van absolute fouten
- Noot
Soorten fouten
Je kan een onderscheid maken tussen drie soorten fouten: de absolute, de relatieve en de procentuele fout.Absolute fout (AF)
De absolute fout van een meetresultaat is de kleinste schaalverdeling van het meetinstrument waarmee het meetresultaat werd verkregen. Bijvoorbeeld: de kleinste schaalverdeling op een maatcilinder van 100 mL is 1 mL. Indien je dus 50 mL water afmeet met zo'n maatcilinder, dan is de absolute fout op dit volume 1 mL. Neem je met diezelfde maatcilinder 20 mL, dan is de absolute fout nog steeds 1 mL. Welk volume je ook afmeet, de absolute fout op volumes afgemeten met deze maatcilinder zal steeds 1 mL zijn. Een absolute fout is dus onafhankelijk van het meetresultaat.- Notatie: meetresultaat ± AF
- Voorbeeld: 50mL ± 1mL
Relatieve fout (RF)
De relatieve fout van een meetresultaat is de absolute fout van dit meetresultaat gedeeld door de waarde van het meetresultaat. De relatieve fout is dus wel afhankelijk van het meetresultaat.Stel dat je 50 mL afmeet met de maatcilinder van 100 mL, dan is de relatieve fout op deze meting:
- 1 mL/50 mL = 0.02
Als je 10 mL afmeet met dezelfde maatcilinder, dan is de relatieve fout:
- 1 mL/10 mL = 0.1
De relatieve fout zal dus sterk toenemen wanneer de waarde van het meetresultaat lager is.
Procentuele fout (PF)
De procentuele fout is de relatieve fout vermenigvuldigd met 100.- Bij het nemen van 50 mL met de maatcilinder is de relatieve fout 0.02. De procentuele fout is hier dus 0.02 × 100 = 2%
- Bij het nemen van slechts 10 mL met deze maatcilinder loopt de procentuele fout al op tot 0.1 × 100 = 10%.
Foutenanalyse bij berekeningen
De absolute fout van een som/verschil
Voorbeeld 1: Je neemt 50 mL water met een maatcilinder met een AF van 1 mL. Je neemt met dezelfde maatcilinder ook 20 mL en je voegt beide volumes samen. Zonder foutenanalyse noteer je het totale volume als 50 mL + 20 mL =70 mL. Maar wat is de AF op dit totale volume?Op beide volumes heb je een AF van 1 mL. De exacte waarde van het eerste volume ligt dus tussen de 49 en de 51 mL De exacte waarde van het tweede volume ligt tussen de 19 en 21 mL
- De som van beide volumes kan dus maximaal 72 mL zijn en minimaal 68 mL.
- De AF is dus 2 mL, de som van de absolute fouten van de twee meetresultaten.
Het berekend resultaat dient dus genoteerd te worden als 70 ± 2 mL De RF op deze berekening is 2 mL/70 mL = 0.03 en de PF 3%.
Besluit: Indien voor een berekening de som of het verschil van twee of meerdere meetresultaten moet worden genomen, dan is de absolute fout van deze som of verschil gelijk aan de som van de absolute fouten van de verschillende meetresultaten.
- AF (meetresultaat 1 + meetresultaat 2) = AF (meetresultaat 1) + AF (meetresultaat 2)
- AF (meetresultaat 1 - meetresultaat 2) = AF (meetresultaat 1) + AF (meetresultaat 2)
De relatieve fout (procentuele fout) van een product/quotiënt
Voorbeeld 2: Je meet de lengte en de breedte van een kamer met een plooimeter met als kleinste schaalverdeling 1 cm. De absolute fout op een afmeting die je bepaald met deze plooimeter is dus 1 cm. De lengte van de kamer is 4.00 m en de breedte van de kamer is 5.00 m De oppervlakte van de kamer is dus: 4.00 m × 5.00 m = 20.0 m2De waarde van de lengte ligt tussen de 3.99 m en de 4.01 m. De waarde van de breedte ligt tussen de 4.99 m en de 5.01 m.
- De minimale waarde die je dus kan meten met de plooimeter is 19.9 m2 en de maximale waarde is 20.1 m2. Het resultaat heeft dus een AF van 0.1 m2 en een RF van 0.1 m2/20 m2 = 0.005 en dus een PF van 0.5%
Je kan hier niet besluiten dat de absolute van het rekenresultaat de som is van de absolute fouten van de meetresultaten. Dit kan ook niet daar de eenheid van het berekende resultaat (m2) anders is dan dat van de meetresultaten (m). Wel kan je hiervoor rekenen met de RF en de PF.
- RF van de eerste meting: 0.01m/4.00m = 0.003
- RF van de tweede meting: 0.01m/5.00m = 0.002
- De som van beide relatieve fouten is dus 0.005 zoals boven berekend.
Besluit: Indien voor een berekening twee of meerdere meetresultaten met elkaar vermenigvuldigd of door elkaar gedeeld dienen te worden, dan is de relatieve fout van dit product of quotiënt gelijk aan de som van de relatieve fouten van de verschillende meetresultaten.
- RF (meetresultaat 1 × meetresultaat 2) = RF (meetresultaat 1) + RF (meetresultaat 2)
- RF (meetresultaat 1 / meetresultaat 2) = RF (meetresultaat 1) + RF (meetresultaat 2)
De relatieve fout van een macht
Voorbeeld 3: Je berekent de inhoud van een kubus. De zijden werden gemeten met een meetlat met als kleinste schaalverdeling 1 mm en ze zijn 3.2 cm lang. De relatieve fout op de afmeting van een zijde is 0.1 cm/3.2 cm = 0.03- Inhoud van een kubus= z3 = 3.2 cm × 3.2 cm × 3.2 cm = (3.2)3 cm3
- Kleinste waarde: (3.1)3 cm3 = 30 cm3
- Grootste waarde: (3.3)3 cm3 = 36 cm3
- RF = 3/33 = 0.09 wat de som is van de RF van de drie zijdemetingen.
Besluit: Indien voor een berekening een meetresultaat tot een macht dient te worden verheven, dan is de relatieve fout op dit rekenresultaat de waarde van de macht vermenigvuldigd met de relatieve fout van het meetresultaat.
- RF(meetresultaatn) = n × RF (meetresultaat)
Eigenlijk kan dit rechtstreeks aan de relatieve fout van een product worden gekoppeld:
b.v. (n = 4): RF(meetresultaat × meetresultaat × meetresultaat × meetresultaat) = RF (meetresultaat) + RF (meetresultaat) + RF (meetresultaat) + RF (meetresultaat) = n × RF (meetresultaat)
Voorbeeld van een wetenschappelijk onderzoek: bepaling van de dichtheid van een vloeistof
Je bepaalt de dichtheid van een vloeistof.- Je neemt hiervoor 20 mL van de vloeistof met de reeds vernoemde maatcilinder van 100 mL. De relatieve fout van deze meting is 1 mL/20 mL = 0.05 en de procentuele fout dus 5%.
- Van dit volume vloeistof bepaal je de massa met een weegschaal met een nauwkeurigheid van 0.1 g. Op de weegschaal wordt een massa van 20,0 g afgelezen. De relatieve fout van deze massabepaling is 0.1 g/20 g = 0.005. De procentuele fout is dus 0.5%.
- Om de dichtheid van de vloeistof te bepalen, dien je de massa te delen door het volume: 20,0 g/20 mL = 1.0 g/mL.
- De relatieve fout van deze meting is 0.05 + 0.005 = 0.055 of een procentuele fout van 5.5%.
Grafische weergave van absolute fouten
Om de waarde van een wetenschappelijk onderzoek te kennen, is het noodzakelijk om in een grafische voorstelling van de meetresultaten ook de absolute fouten weer te geven.Stel dat je de dichtheid van water bepaalt door van verschillende volumes water de massa te bepalen. Je kan van de meetresultaten een grafiek opstellen (figuur 1). Deze grafiek zegt echter niets over de nauwkeurigheid van de metingen. Hiervoor moet je ook de absolute fouten weergeven aan de hand van foutenbalkjes.
Stel dat je voor het onderzoek een weegschaal gebruikt die tot op 0.1 g (= AF op de massa) kan afwegen en een maatcilinder die tot op 1 mL (= AF op het volume) afmeet. Indien je deze absolute fouten in de grafiek weergeeft, krijg je figuur 2.
Je kan voor het onderzoek ook een weegschaal met een nauwkeurigheid van 0.01 g en een pipet gegradueerd tot op 0.1 mL gebruiken. Indien je nu de absolute fouten in je grafiek uitzet, krijg je figuur 3.
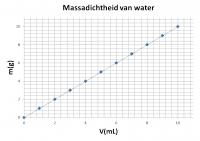 Figuur 1
Figuur 1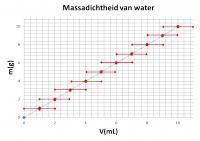 Figuur 2
Figuur 2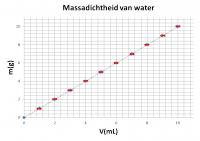 Figuur 3
Figuur 3Op basis van figuur 1 krijg je dus geen enkel idee van de nauwkeurigheid van de metingen. De vergelijking van figuren 2 en 3 geeft duidelijk aan dat de meetresultaten voorgesteld in figuur 3 veel nauwkeuriger zijn dan die voor figuur 2. Hieruit kan je besluiten dat het onderzoek met de nauwkeuriger meetinstrumenten meer waarde heeft.
Noot
Voor het rekenen met meetresultaten dien je rekening te houden het significante cijfers.© 2020 - 2024 Guust2016, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Berekening van de procentuele mogelijke meetfoutWanneer we dingen opmeten, stuiten we steeds weer op beperkingen van onze meetapparatuur. Met deze wijsheid op zak is he…
Berekening van de procentuele mogelijke meetfoutWanneer we dingen opmeten, stuiten we steeds weer op beperkingen van onze meetapparatuur. Met deze wijsheid op zak is he…
 Fout gemaakt? Fouten toegeven, wat is het voordeel?Wat is het grote voordeel om je eigen fouten toe te geven? Welke wonderen ontstaan er als je je eigen gemaakte fouten to…
Fout gemaakt? Fouten toegeven, wat is het voordeel?Wat is het grote voordeel om je eigen fouten toe te geven? Welke wonderen ontstaan er als je je eigen gemaakte fouten to…
 Rekenen met meetresultaten: significante cijfersEen meetresultaat wordt steeds weergegeven door een getalwaarde gevolgd door een eenheid. De nauwkeurigheid van een meet…
Rekenen met meetresultaten: significante cijfersEen meetresultaat wordt steeds weergegeven door een getalwaarde gevolgd door een eenheid. De nauwkeurigheid van een meet…
 Fout negatieve test of uitslagWanneer er een test wordt gedaan, volgt er een uitslag. Deze uitslag kan zowel positief als negatief zijn. In de medisch…
Fout negatieve test of uitslagWanneer er een test wordt gedaan, volgt er een uitslag. Deze uitslag kan zowel positief als negatief zijn. In de medisch…
 Wat is het verband tussen darmbacteriën en autisme?Het menselijk lichaam biedt huisvesting aan een grote variëteit aan micro-organismen. Grote aantallen bacteriën bevolken…
Wat is het verband tussen darmbacteriën en autisme?Het menselijk lichaam biedt huisvesting aan een grote variëteit aan micro-organismen. Grote aantallen bacteriën bevolken…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Kreatikar, Pixabay
Guust2016 (74 artikelen)
Laatste update: 21-10-2020
Rubriek: Wetenschap
Subrubriek: Onderzoek
Bronnen en referenties: 1
Laatste update: 21-10-2020
Rubriek: Wetenschap
Subrubriek: Onderzoek
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.