Speel een verrassend wiskundig spel: Game of life
 Met wiskunde kun je leuke dingen doen. Het bekende Game of Life, dat in 1970 door de wiskundige John Conway werd bedacht fascineerde de wereld. Talloze patronen bleken mogelijk, die in een simpel tweedimensionaal rooster geboren werden, leefden en dood gingen. Zelfs bewegende voorwerpen zag je in opvolgende generaties door je rooster schuiven. Game of Life houdt nog steeds heel wat mensen bezig!
Met wiskunde kun je leuke dingen doen. Het bekende Game of Life, dat in 1970 door de wiskundige John Conway werd bedacht fascineerde de wereld. Talloze patronen bleken mogelijk, die in een simpel tweedimensionaal rooster geboren werden, leefden en dood gingen. Zelfs bewegende voorwerpen zag je in opvolgende generaties door je rooster schuiven. Game of Life houdt nog steeds heel wat mensen bezig!
John Conway
De Britse wiskundige John Conway werd op 26 december 1937 in Liverpool geboren. Conway studeerde aan de Universiteit van Cambridge (Engeland) en is later zelf ook wiskunde gaan doceren als professor aan de Universiteit van Princeton (Verenigde Staten). Conway is actief op verschillende gebieden binnen de wiskunde en heeft een groot aantal werken gepubliceerd. Eén van zijn werkterreinen is het onderzoek naar cellulaire automata, waaronder de Game of Life.Een cellulaire automaat
Een cellulaire automaat, dat klinkt ingewikkelder dan het in feite is. Een cellulaire automaat is een model uit de automatentheorie dat in de berekenbaarheidstheorie in de wiskunde en in de theoretische biologie wordt gebruikt. In een dergelijk model wordt gebruik gemaakt van een één- of meerdimensionaal raster van cellen, met een oneindig aantal toestanden, ook wel generaties genoemd. De eigenschappen van elke cel zijn bepalend voor de eigenschappen van die cel in de volgende generatie. Als je generaties elkaar laat opvolgen, dan zie je processen en patronen ontstaan die regelmatig lijken op wat je in de natuur ook kunt vinden, zoals groeiprocessen van kristallen of koralen. En natuurlijk speelt dit alles ook een rol in de digitale wereld. Laten we eens kijken hoe dat voor de Game of Life uitpakt.Game of Life
Laten we het allemaal maar eens concreter maken. Stel je voor, je hebt een tweedimensionaal rooster, zoals een stuk ruitjespapier, of een dambord. Elk hokje of vakje noemen we een cel. Een cel kan twee toestanden hebben: hij is dood of levend. Een dode cel ziet er uit als een leeg vakje, een levende cel is een gevuld, dus ingekleurd vakje. De Game of Life komt letterlijk tot leven als er meerdere generaties zijn. De toestand van de cellen (dood of levend) is bepalend voor de toestand van de cellen in de volgende generatie. Er zitten natuurlijk wel een paar regels aan vast.De regels
Regels zijn in de Game of Life nodig, om te voorkomen dat het hele speelveld levend (gevuld) raakt, of helemaal dood (alles leeg). Conway bedacht de volgende afspraken en regels:- Een cel kan levend of dood zijn. Een dode cel is leeg, een levende cel is gevuld.
- Een cel heeft acht buurcellen, die allemaal aan deze cel raken. Dat is ofwel aan één van de vier zijden, ofwel aan één van de vier hoekpunten.
- Als twee of drie buurcellen van een bepaalde cel gevuld (levend) zijn, dan blijft deze cel in de volgende generatie bestaan, blijft dus leven en ingekleurd.
- Als vier of meer buurcellen van een bepaalde cel gevuld zijn (levend), dan is er sprake van overbevolking en gaat deze cel dood (wordt leeg)
- Als een lege (dode) cel drie gekleurde (levende) buurcellen heeft, niet meer of minder, dan wordt in deze cel leven geboren: in de volgende generatie is deze cel ingekleurd.
- Als een cel géén of maar één levende buurcel heeft, dan gaat deze cel in de volgende generatie dood.
De regels in de praktijk
Laten we de regels eens in praktijk gaan brengen. Je ziet hier een stukje van het grid, waarin enkele cellen zijn ingekleurd. Wat gaat er met al deze cellen gebeuren?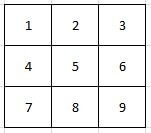 Celnummering die in onderstaand voorbeeld gebruikt worden
Celnummering die in onderstaand voorbeeld gebruikt worden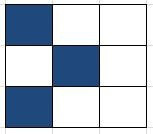 Uitgangspunt met ingevulde cellen
Uitgangspunt met ingevulde cellen- Cel 1. Deze levende cel heeft één levende buurcel. Dat is te weinig, deze cel gaat in de volgende generatie dood.
- Cel 2. Deze dode cel heeft twee levende buurcellen. Dat is niet genoeg voor nieuw leven, de cel blijft in de volgende generatie leeg.
- Cel 3. Deze dode cel heeft één levende buurcel, en blijft dus leeg in de volgende generatie.
- Cel 4. Deze dode cel heeft drie levende buurcellen, in de volgende generatie is deze cel gekleurd.
- Cel 5. Deze levende cel heeft twee levende buurcellen en blijft in de volgende generatie bestaan.
- Cel 6. Deze dode cel heeft één levende buurcel en blijft dus leeg in de volgende generatie.
- Cel 7. Deze levende cel heeft één levende buurcel. In de volgende generatie is deze cel leeg.
- Cel 8. Deze dode cel heeft twee levende buurcellen. In de volgende generatie blijft deze cel leeg.
- Cel 9. Deze dode cel heeft één levende buurcel en blijft in de volgende generatie leeg.
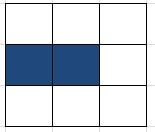 Na één generatie
Na één generatieBijzondere patronen in verschillende generaties
Door vele generaties te laten doorlopen worden soms bijzondere figuren en patronen ontdekt. Sommige daarvan zien er uit als een bloem, ruimteschip en hebben dan ook namen die hieraan refereren. Inmiddels zijn er bijna 800 verschillende figuren ontdekt, waarvan een aantal bijzonder stabiel zijn of zich over het rooster lijken te bewegen. Een bijzonder stabiel patroon is bijvoorbeeld een blokje van 4 gevulde cellen. Als je de regels toepast zie je dat dit blokje er in elke generatie precies hetzelfde uitziet. Dan zijn er nog figuren, die nieuwe patronen laten ontstaan.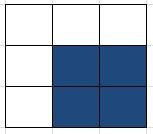 Een bijzonder stabiel en statisch patroon
Een bijzonder stabiel en statisch patroonOok bijzonder zijn de bewegende patronen, zoals de glider. Pas je de regels toe op dit figuur, dan zie je het patroon zich na een paar generaties exact herhalen, maar dan schuin onder zijn voorganger. Laat je de generaties doorlopen, dan zie je dit figuur uiteindelijk van het rooster afschuiven.
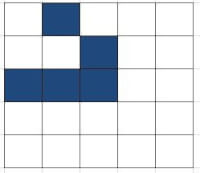 Glider, generatie één
Glider, generatie één Glider, generatie twee
Glider, generatie twee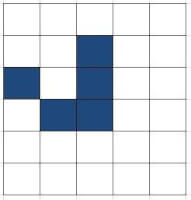 Glider, generatie drie
Glider, generatie drie Glider, generatie vier
Glider, generatie vier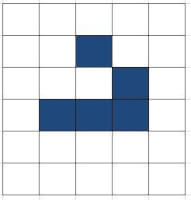 Glider, generatie vijf: precies één vakje naar rechts en één naar beneden t.o.v. het origineel
Glider, generatie vijf: precies één vakje naar rechts en één naar beneden t.o.v. het origineelGame of Life zit vol verrassingen
Met zoveel verschillende figuren is er in Game of Life altijd wel iets te beleven, er ontstaan verrassende patronen die zichzelf creëren, vernietigen of een bijzonder interactie met elkaar aangaan. Het is altijd de moeite waard om hiermee te experimenteren. Wie weet ontdek je nieuwe figuren, patronen of bewegingen.Hoe speel je Game of Life?
Je kunt game of Life spelen met een flinke stapel ruitjespapier. Het is lastig dat je voor elke generatie weer een heleboel moet inkleuren. Je kunt ook gebruik maken van een dambord (of een reeks damborden), waar je levend of dood kunt aangeven door een damsteen wel of juist niet te plaatsen. Maar natuurlijk wordt tegenwoordig bijna altijd een computer gebruikt om de Animaties van game of Life tot leven te wekken. Dat voorkomt een heleboel tekenwerk en zorgt voor aanmerkelijk minder fouten. Je kunt Game of Life in allerlei vormen op verschillende plaatsen op het internet aantreffen. Soms betreft het downloadbare varianten, soms online versies. Een voorbeeld van zo'n online versie vind je hier.© 2015 - 2025 Hansvg, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Reclame in online gamesReclame in computerspellen bestaat bijna net zo lang als er computergames zelf zijn. De eerste vormen van reclame in gam…
Reclame in online gamesReclame in computerspellen bestaat bijna net zo lang als er computergames zelf zijn. De eerste vormen van reclame in gam…
 Veilig drinkwater dankzij de Life-StrawElke dag sterven er wereldwijd 6000 kinderen door het drinken van verontreinigd water. Ze sterven aan tyfus, cholera, dy…
Veilig drinkwater dankzij de Life-StrawElke dag sterven er wereldwijd 6000 kinderen door het drinken van verontreinigd water. Ze sterven aan tyfus, cholera, dy…
 Cheats, hints, eastereggsCheats, hints en eastereggs (codes) zijn er voor bijna alle soorten games (spelletjes). Wat kun je met cheats, easteregg…
Cheats, hints, eastereggsCheats, hints en eastereggs (codes) zijn er voor bijna alle soorten games (spelletjes). Wat kun je met cheats, easteregg…
 Een bijzondere fractal: de driehoek van SierpinskiDe Poolse wiskundige Waclaw Sierpinski verrichte baanbrekend werk in de wiskunde, met name in de verzamelingenleer. Voor…
Een bijzondere fractal: de driehoek van SierpinskiDe Poolse wiskundige Waclaw Sierpinski verrichte baanbrekend werk in de wiskunde, met name in de verzamelingenleer. Voor…
Gerelateerde artikelen
De geschiedenis van consoles: derde en vierde generatieIn de tijd dat de consoles van de derde en vierde generatie uitkwamen domineerde Nintendo de internationale markt van co…
Het algoritme: Theoretisch hulpmiddel of dagelijkse kost?De term algoritme wordt vaak gebruikt in de lessen wiskunde, logica en computerwetenschappen, zonder dat de studenten ec…
Bronnen en referenties
- https://nl.wikipedia.org/wiki/Game_of_Life
- http://www.conwaylife.com/wiki/Main_Page
- http://www.conwaylife.com/
- https://nl.wikipedia.org/wiki/Cellulaire_automaat
- https://nl.wikipedia.org/wiki/John_Conway
Hansvg (513 artikelen)
Laatste update: 19-11-2020
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Laatste update: 19-11-2020
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.