Stelling van Pythagoras

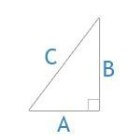Met de stelling van Pythagoras kun je de lengtes van de zijden van een rechthoekige driehoek berekenen. De stelling is relatief eenvoudig maar wordt ook nu nog erg veel gebruikt door de wetenschap.

De stelling

Als je de lengtes van twee van de drie zijdes van een rechthoekige driehoek weet kun je de derde berekenen. De stelling van Pythagoras luidt als volgt:
a² + b² = c²

In de bovenstaande afbeelding kun je zien dat de zijdes a en b aan de rechte hoek liggen. Vandaar dat ze ook rechthoekzijdes heten. De ‘schuine’ zijde, ook wel hypotenusa genoemd, ligt recht tegenover de rechte hoek.

Het bewijs

Zonder een kloppend bewijs is een stelling in de wetenschap onjuist. Zo heeft dus ook de stelling van Pythagoras een bewijs. a² kun je je voorstellen als een vierkant met de oppervlakte van a*a. Zo geldt dat ook bij b² en c². Als je dan gaat opmeten wat de absulute oppervlaktes van a², b² en c² zijn, zul je opmerken dat de oppervlaktes van de vierkanten op a en b samen precies even groot zijn als de vierkant op de c zijde.

Gebruik

Het tegenovergestelde van het kwadraat is de wortel. Als je de lengtes van a en b weet kun je de lengte van de c-zijde dus zo berekenen: c = √(a² + b²) Zo kun je de formule zo ombouwen dat je iedere zijde kunt berekenen als je de lengtes van twee andere zijdes weet. © 2006 - 2008 Willem, gepubliceerd in Wiskunde (Wetenschap) op 04-10-2006. Het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming van Willem is vermenigvuldiging van dit artikel verboden. Meer...

Verwante artikelen

• De Stelling van Fermat: De Franse wiskundige Pierre de Fermat leefde in de 17de eeuw. Wiskunde was een hobby voor hem, eigenlijk was hij jurist. Hij hield zich graag bezig met getallenleer. Voor allerlei mog…
• Ruimtemeetkunde: Je komt het de hele dag tegen, waarschijnlijk onbewust; ruimtemeetkunde. Dit heeft alles te maken met de aanzichten van dingen, afstanden, de stelling van Pythagoras, etc.
• Stelling van Thales: De stelling van Thales is geformuleerd door Thales van Milete. De wiskundige en filosoof gebruikte deze meetkundige stelling om de hoogte van piramides te berekenen.
• Hoe schrijf je een Betoog: Veel mensen hebben een probleem met het schrijven van een goed betoog. Wat is een betoog eigenlijk? Het draait allemaal om structuur aanbrengen in je tekst en je aan je hoofddoel h…
• Griekse Oostelijk Egeïsche eilanden, Samos: Vlak voor de Turkse kust ligt het op drie na grootste eiland van de Egeïsche archipel. Volgens de Grieken zelf een populaire vakantiebestemming. Het is een uiterma…