Stelling van Thales

De stelling van Thales is geformuleerd door Thales van Milete. De wiskundige en filosoof gebruikte deze meetkundige stelling om de hoogte van piramides te berekenen.

De stelling van Thales

1. Evenwijdige rechten snijden van twee andere rechten evenredige stukken af.
2. Een driehoek ingeschreven in een cirkel, waarvan één zijde de diameter van de cirkel vormt, is een rechthoekige driehoek.

Stelling van Thales voorbeelden

1. Cabri Java Applet van de stelling
2. Cabri Java Applet van de omgekeerde stelling

Uit de stelling volgt:
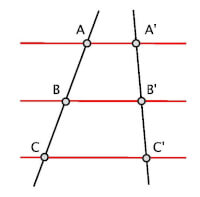
De verhouding van |A'B'| op |AB|
is gelijk aan de verhouding van |B'C'| op |BC|
is gelijk aan de verhouding van |A'C'| op |AC|

De legende van Thales

Thales werd al beschouwd als één der Zeven Wijzen en voorspelde ooit een zonsverduistering. De farao vroeg hem de hoogte van de piramide van Cheops te bepalen.

Hij had zo goed als niets nodig, met een stok zou hij in z'n opdracht slagen. Hij gaat naast de piramide staan en kijkt naar de driehoekige schaduw van de piramide. Driehoeken en cirkels zijn bijzondere objecten voor hem. Je ziet ze zelden in de natuur, maar toch schuilt er heel wat achter. Hoe verder de zon naar het zuiden gaat, hoe groter de schaduw. Thales gaat in de zon staan en zet de stok in het zand, die ook een schaduw werpt. Nu alleen even wachten.

Het moment is aangebroken als de stok even groot is als de schaduw van de stok. Want op dat moment is de lengte van de schaduw gelijk aan de hoogte. Proportie is gelijk aan proportie.