Berekening van de procentuele mogelijke meetfout

Wanneer we dingen opmeten, stuiten we steeds weer op beperkingen van onze meetapparatuur. Met deze wijsheid op zak is het nuttig om een idee te krijgen van hoe groot een meetfout kan zijn.

Begripvorming

Welk meetinstrument we ook gebruiken, steeds weer worden we geconfronteerd met de onnauwkeurigheid ervan. Nemen we als voorbeeld een meetlat. De meeste meetlatten zijn zo ontworpen dat de kleinste schaaleenheid die we er aantreffen overeenkomt met 0,1 cm. De meetlat zelf heeft een centimeterverdeling. Welnu, hiervan zegt men dat het meetresultaat een nauwkeurigheid heeft van 0,1 cm (de kleinste schaaleenheid). Dit zowel naar onder als naar boven toe. Meet men bijvoorbeeld met de meetlat een waarde van 13,8 cm; dan noteert men dit als volgt: 13,8 ± 0,1 cm. Hieruit kunnen we afleiden dat het werkelijke meetresultaat ligt tussen 13,7 en 13,9 cm.

De procentuele mogelijke meetfout

De procentuele mogelijke meetfout is de onnauwkeurigheid gedeeld door de gemeten waarde, vermenigvuldigd met 100%. Terugkerend op onze meting van daarnet betekent dit: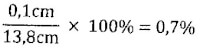

Wanneer we een gemeten waarde aflezen weten we niet altijd met welke nauwkeurigheid deze waarde moet bekeken worden. In dat geval nemen we aan dat de onnauwkeurigheid in het meetresultaat gelijk is aan één eenheid in het meest rechtse cijfer van de gemeten waarde. Dit zowel naar onder als naar boven toe. Krijgen we bijvoorbeeld als meetwaarde 53,6 m; dan is de onnauwkeurigheid ± 0,1 m en noteren we: 53 ± 0,1 m.

Voorbeelden

Wat is de procentuele mogelijke meetfout in het meetresultaat 16,5m?

We nemen aan dat de meetfout één decimaal van het meest rechtse cijfer bedraagt. Dit is dan ± 0,1m.
De procentuele mogelijke meetfout is dan:

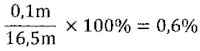
Bepaal de procentuele mogelijke meetfout in het volgende meetresultaat: 39,47 ± 0,28s.

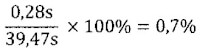
De procentuele mogelijke meetfout is:

Een bol heeft een straal r = 1,73 ± 0,04m. Bereken het volume van de bol en bepaal de procentuele mogelijke meetfout.

Het volume van een bol is:

De meetfout is ± 0,04m. We krijgen als ondergrens van de meting: 1,73m - 0,04m = 1,69m. Dit geeft dan:

En als bovengrens: 1,73m + 0,04m = 1,77m. Dit geeft dan:

Het eindresultaat is dan: 21,70 ± 1,50m³. De procentuele mogelijke meetfout is:

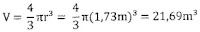
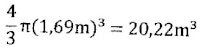
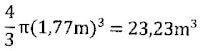
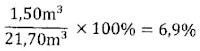
Significante cijfers

Definitie
De uitwerkingen die hierboven vermeld staan brengen een ander probleem naar voor, namelijk dat van het aantal significante cijfers in een getalwaarde. Welnu, het aantal cijfers in een getalwaarde waar we zeker van mogen zijn, noemen we de significante cijfers van deze getalwaarde.

Werkwijze
Hier zijn twee belangrijke regels van toepassing. Deze zijn:
[OLIST]Bij meetresultaten mag men niet meer cijfers opnemen in het resultaat, dan het aantal significante cijfers in de minst nauwkeurige factor van het meetresultaat.
De uitkomst van een som, verschil, vermenigvuldiging of deling mag niet meer cijfers bevatten dan de getalwaarde met het minst aantal significante cijfers dat in de berekening is gebruikt.[/OLIST]

Voorbeelden
[OLIST]Hoeveel significante cijfers hebben de volgende getallen: a) 682; b) 55,06; c) 0,083; d) 3500; e) 0,0000047; f) 551,70 en g)1,6.

a) 682: Drie significante cijfers, namelijk 6, 8 en 2.

b) 55,06: Vier significante cijfers, namelijk 5, 5, 0 en 6.

c) 0,083: Twee significante cijfers, namelijk 8 en 3.

d) 3500: Vermoedelijk twee significante cijfers, namelijk 3 en 5.

e) 0,0000047: Twee significante cijfers, namelijk 4 en 7.

f) 551,70: Vijf significante cijfers, namelijk 5, 5, 1, 7 en 0.

g) 1,6: Twee significante cijfers, namelijk 1 en 6.

Een driehoek heeft een basis van 3,75cm en een hoogte van 6,5cm. Bereken de oppervlakte van de driehoek en druk het eindresultaat uit in het juiste aantal significante cijfers. De oplossing die we hier zoeken zal uit twee significante cijfers moeten bestaan, daar het getal met het minst aantal significante cijfers uit de opgave (6,5) ook uit twee significante cijfers bestaat (3,75 bestaat namelijk uit drie significante cijfers). De oppervlakte A van de driehoek wordt dus:[/OLIST]