Bereken brekingsindex en grenshoek met de wet van Snellius
 Als licht eerst door lucht gaat en dan door een doorzichtige stof verandert de lichtstraal van richting. Dan zeg je dat de lichtstraal wordt gebroken. Met de formule voor de brekingsindex kun je voorspellen hoe de lichtstraal gebroken wordt. Als je de hoek waaronder de lichtstraal invalt op de doorzichtige stof steeds groter maakt wordt op een bepaald moment de lichtstraal niet meer gebroken maar teruggekaatst. Dit heet reflectie. Op dat moment laat je licht invallen met de grenshoek. Maar hoe kun je nu eigenlijk die grenshoek en de brekingsindex berekenen?
Als licht eerst door lucht gaat en dan door een doorzichtige stof verandert de lichtstraal van richting. Dan zeg je dat de lichtstraal wordt gebroken. Met de formule voor de brekingsindex kun je voorspellen hoe de lichtstraal gebroken wordt. Als je de hoek waaronder de lichtstraal invalt op de doorzichtige stof steeds groter maakt wordt op een bepaald moment de lichtstraal niet meer gebroken maar teruggekaatst. Dit heet reflectie. Op dat moment laat je licht invallen met de grenshoek. Maar hoe kun je nu eigenlijk die grenshoek en de brekingsindex berekenen?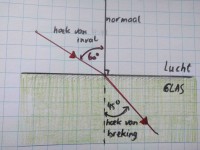 Afbeelding 1. Normaal, hoek van inval en hoek van breking
Afbeelding 1. Normaal, hoek van inval en hoek van brekingNormaal, hoek van inval en hoek van breking
Op afbeelding 1 staan de normaal, de hoek van inval en de hoek van breking aangegeven. De lichtstraal (rode pijl) komt van links en beweegt naar rechts. Eerst bevindt de lichtstraal zich in lucht, daarna gaat de lichtstraal verder in glas (met groen aangegeven). De normaal van een vlak staat loodrecht (onder een hoek van 90 graden) op dat vlak. De hoek van inval is de hoek tussen de invallende lichtstraal en de normaal. Hier is de hoek van inval 60 graden. De hoek van breking is de hoek tussen de gebroken lichtstraal en de normaal. De hoek van breking is hier 45 graden.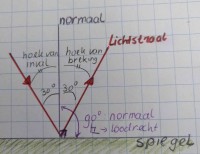 Afbeelding 2. Hoek van inval = hoek van terugkaatsing bij reflectie
Afbeelding 2. Hoek van inval = hoek van terugkaatsing bij reflectieOptische eigenschappen
Als er een lichtstraal op een voorwerp valt zijn er 3 mogelijkheden:[OLIST]De lichtstraal verandert van richting. Dan zeg je dat de lichtstraal wordt gebroken (de hoek van breking is dan anders dan de hoek van inval). Zie afbeelding 1.
Als je de hoek van inval steeds groter maakt kan de lichtstraal gereflecteerd worden. De lichtstraal wordt dan teruggestuurd onder dezelfde hoek. Op dat moment is de hoek van inval gelijk aan de hoek van terugkaatsing (i=t). Denk hierbij aan een spiegel. Zie afbeelding 2.
De lichtstraal wordt geabsorbeerd (opgenomen).
[/OLIST]
Wat is de brekingsindex: de wet van Snellius
Als de lichtstraal gebroken wordt kun je de brekingsindex uitrekenen. De brekingsindex is een verhoudingsgetal, het geeft de snelheid van het licht in de verschillende stoffen aan. In dit voorbeeld gebruiken we een lichtstraal die van lucht naar gewoon glas gaat. De formule voor de brekingsindex wordt ook wel eens de wet van Snellius genoemd.Formule voor de brekingsindex
NA→B = sin iA/sin rB
Waarbij:
- iA is de hoek van inval in graden
- rB is de hoek van breking in graden
- NA→B is de brekingsindex van stof A naar stof B
Berekening brekingsindex
Bij de bovenste tekening zie je dat de hoek van inval 60 graden is, de hoek van breking is 45 graden.NA→B = sin iA/sin rB = sin 60 /sin 45 = 0,86/0,707= 1,22
Tabel met brekingsindexen
Als je in BINAS in de tabel van de brekingsindexen kijkt (tabel 18 A) zie je bij de vaste stoffen dat gewoon glas een brekingsindex van 1,51 heeft. Nlucht→glas is 1,51. De brekingsindexen in tabel 18 A gelden altijd voor de overgang van lucht naar een andere doorzichtige stof. Kijk ook naar de golflengte van het licht die bij deze brekingsindex hoort. De brekingsindex van gewoon glas is bij een golflengte van 687 nm (rood licht) 1,51. Voor 486 nm (blauw licht) is de brekingsindex 1,52. Als de lichtstraal nu van gewoon glas naar lucht gaat (van B naar A) geldt:Nglas→lucht = 1/ Nlucht→glas = 1/1,51= 0,66.
Je kunt dus de brekingsindex van de stof naar lucht uitrekenen met het omgekeerde van de brekingsindex van lucht naar die stof.
Dus: NB→A= 1/NA→B.
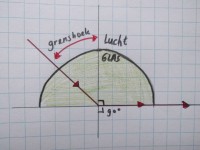 Afbeelding 3. Hoek van inval en hoek van breking (90 graden) bij de grenshoek
Afbeelding 3. Hoek van inval en hoek van breking (90 graden) bij de grenshoekBerekening grenshoek
Stel dat je nu wil weten wat de grenshoek is bij de overgang van gewoon glas naar lucht. Bij reflectie is de hoek van breking gelijk aan de hoek van inval (i = t). De grenshoek is de hoek van inval van een lichtstraal waarbij de gebroken lichtstraal met een hoek van 90 graden wordt gebroken. De lichtstraal scheert dan langs het oppervlak. Je ziet de gebroken lichtstraal een hoek van 90 graden met de normaal maken (de horizontale rode pijl die naar rechts wijst). De hoek van breking is hier 90 graden. Voor de sinus van de hoek van breking kun je dan sinus 90 = 1 invullen. Dus Nglas→lucht = sin hoek van inval/sin hoek van breking = 1 / Nlucht→glas .We hadden reeds opgezocht dat de brekingsindex voor gewoon glas 1,51 is. Dan is de brekingsindex voor glas naar lucht: sin grenshoek = 1/1,51. Hieruit volgt als je inverse sinus 1/1,51 op je rekenmachine invoert (sin-1) dat er voor de grenshoek 41,5 graden uitkomt. Dit betekent als de lichtstraal vanuit glas naar lucht met een hoek van inval groter dan 41,5 graden invalt, dat dan de lichtstraal wordt gereflecteerd (zoals bij afbeelding 2). Bij precies 41,5 graden zul je zien dat de lichtstraal langs het glasoppervlak scheert (zoals bij afbeelding 3). Bij minder dan 41,5 graden als hoek van inval zal de lichtstraal gebroken worden en aan de andere kant van het glas naar buiten treden (zoals bij afbeelding 1).