Eenparige cirkelbeweging: snelheid, toerental en frequentie

Een eenparige cirkelbeweging is een beweging van een voorwerp dat met een constante snelheid in een cirkelbaan draait. Bij eenparige cirkelbewegingen kun je denken aan de was die in een centrifuge ronddraait of een kind dat in een draaimolen zit. Maar welke afstand legt zo’n voorwerp nu eigenlijk in een bepaalde tijd af en wat betekent het toerental bij een wasmachine?

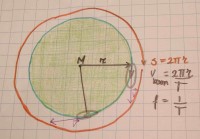Afbeelding 1: Eenparige cirkelbeweging van voorwerp V

De afgelegde weg bij een eenparige cirkelbeweging

Bij een eenparige cirkelbeweging beweegt een voorwerp V in een cirkelbaan met een constante snelheid. De afstand van het middelpunt M van de cirkel tot aan het voorwerp V heet de baanstraal (r). Als het voorwerp V één keer rond gaat heeft het een afstand van 2πr afgelegd. We zeggen dan dat de afgelegde weg (s in meters) 2πr is. Dus s = 2πr meter. Het getal π (pi) is ongeveer 3,14. Stel dat de straal van de cirkel 3 meter is. Dan legt het voorwerp V bij één omwenteling 2πr = 2 X π X 3= 2 X 3,14 X 3 = 18,9 meter af. Het getal π staat als het goed is op of onder een knop op je rekenmachine. Dan reken je altijd met de correcte waarde en niet met een afronding.

Vectoren kort uitgelegd

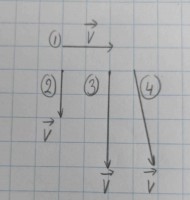Afbeelding 2: een aantal vectoren

Als je wilt aangeven dat de snelheid een grootte en een richting heeft gebruik je de vector v (met een pijl er boven). De grootte wordt aangegeven met de lengte van de vector en de richting geef je aan door de richting van de pijl. De vector werkt vanuit het beginpunt van de pijl. Dit heet het aangrijpingspunt. In de tekening zie je dat de vector v1 en vector v2 dezelfde lengte hebben. Hun richting is echter niet hetzelfde. Dat betekent dat de snelheden van vector v1 en v2 net zo groot zijn, maar een andere richting op werken. De voorwerpen gaan hier een andere kant op, maar hebben wel dezelfde snelheid. Vector v3 wijst dezelfde richting op als v2, maar heeft een dubbele grootte. Dat betekent dat de snelheid van een voorwerp waar vector 3 op werkt dubbel zo groot is en dezelfde richting opgaat als een voorwerp waar vector 2 op werkt. Vector v4 tenslotte, is net zo lang als vector v3, maar wijst een andere kant op. Dus de snelheid van voorwerpen waar vector 3 en vector 4 op werken is hetzelfde, maar ze bewegen in een andere richting.

Richting en grootte van de snelheid bij een eenparige cirkelbeweging

Bij een eenparige cirkelbeweging is de snelheid constant. De lengte van vector v is bij een cirkelbeweging overal hetzelfde. Dit betekent dat de grootte van de snelheid hetzelfde is. De richting van de snelheid blijft echter niet hetzelfde. De vector v staat iedere keer loodrecht op de straal, dus de richting van de snelheid verandert voortdurend. Als je de richting van de snelheid wil weten moet je de raaklijn aan de cirkel tekenen. De vector v heeft dan de richting van de raaklijn aan de cirkel.

Baansnelheid eenparige cirkelbeweging

De baansnelheid is een ander woord voor de snelheid langs de cirkelbaan. De tijd die het voorwerp V nodig heeft om één keer rond te gaan is T (omlooptijd in seconden s).

Formule voor de baansnelheid
v_baan = s / t = afgelegde weg / tijd = 2πr / T (in meter per seconde ms^-1)

Waarbij:

v_baan: de baansnelheid in meter per seconde (in meter per seconde ms^-1)
r: de baanstraal van V in meter (m)
T: de omlooptijd van V in seconden (s)
s: de afgelegde weg van V in meter (m)
t: de tijd in seconden (s)

Rekenvoorbeeld baansnelheid

Bereken de baansnelheid van voorwerp V.
Waarbij

Een voorwerp V draait in 5,3 seconden één keer rond. Dus T = 5,3 seconden.
De straal r van de cirkel is 2,6 meter. Dus r = 2,6 m.

v_baan = s / t = 2πr / T in meter per seconde (ms^-1)
v_baan = 2πr / T = 2π X 2,6 / 5,3 = 3,1 meter per seconde (ms^-1)

Wat is frequentie

Bij een eenparige cirkelbeweging is die tijd die het voorwerp V er over doet om rond te bewegen steeds dezelfde. De snelheid blijft hetzelfde, daarom heet het een eenparige cirkelbeweging. De omloopsnelheid T (in seconden s) is dus constant. Het aantal omlopen per seconde heet de frequentie. De eenheid van frequentie is de hertz (Hz).

Formule voor frequentie
f = 1 / T in s^-1

Waarbij:

f: frequentie in hertz (Hz)
T: omlooptijd in seconden (s)

Rekenvoorbeeld frequentie

Een voorwerp V doet er 5 seconden over om in één keer rond te gaan. Wat is de frequentie van voorwerp V?

Formule voor frequentie
f = 1 / T in s^-1

Waarbij:

f: frequentie in hertz (Hz)
T: omlooptijd in seconden (s)

We vullen voor T 5 seconden in. Dan wordt de formule:
f = 1 / 5 s^-1, dus f = 0,2 hertz.

Toerental

Technische mensen gebruiken nogal eens de term toerental. Dan bedoelen ze het aantal omwentelingen dat voorwerp V in 1 minuut (60 seconden) maakt. Dus als voorwerp V in 1 minuut 20 keer rond gaat is het toerental 20. In het Engels wordt het toerental revolutions per minute (RPM) genoemd.

Rekenvoorbeeld toerental

Stel dat voorwerp V in 5 seconden eenmaal rond gaat. Wat is de RPM van voorwerp V? Let op: RPM is per minuut = 60 seconden. Frequentie is in hertz: per seconde.
RPM= 60 s / 5 s = 12 omwentelingen per minuut. Het toerental is dus 12 revolutions per minute (RPM).