Bereken de gravitatiekracht: de gravitatiewet van Newton
 Isaac Newton heeft als eerste het verband van de gravitatiekracht beschreven. Hij vond dat twee voorwerpen een kracht op elkaar uitoefenen. De kracht die uitgeoefend wordt is afhankelijk van de massa van beide voorwerpen en omgekeerd evenredig met het kwadraat van de afstand van de voorwerpen tot elkaar. Maar hoe bereken je nu eigenlijk de gravitatiekracht?
Isaac Newton heeft als eerste het verband van de gravitatiekracht beschreven. Hij vond dat twee voorwerpen een kracht op elkaar uitoefenen. De kracht die uitgeoefend wordt is afhankelijk van de massa van beide voorwerpen en omgekeerd evenredig met het kwadraat van de afstand van de voorwerpen tot elkaar. Maar hoe bereken je nu eigenlijk de gravitatiekracht?Wat is de gravitatiekracht?
Een andere naam voor gravitatiekracht is zwaartekracht en staat voor een aantrekkingskracht tussen twee of meer massa's gedeeld door het kwadraat van de afstand tot elkaar. Newton was de eerste die dit verband in zijn gravitatiewet beschreef. Als je de gravitatiekracht wil berekenen gebruik je de formule van de gravitatiekracht. Op atomair niveau is deze kracht zeer klein door de minuscule massa's van elektronen, protonen en neutronen. In het heelal en op het niveau van planeten is de gravitatiekracht belangrijk. De gravitatiekracht werkt op ieder voorwerp. De gravitatiekracht zorgt er op aarde voor dat een appel valt. Daarnaast blijft de maan in een baan om de aarde draaien door de gravitatiekracht. Onze aarde blijft weer door de gravitatiekracht in een baan om de zon bewegen.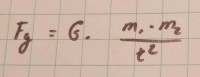 Afbeelding 1: de formule van de gravitatiekracht
Afbeelding 1: de formule van de gravitatiekrachtDe formule van de gravitatiekracht
Fg = (G X m1 X m2) / r2waarbij:
- G = de gravitatieconstante: 6,67 X 10-11 Nm2kg-2 (te vinden in BINAS tabel 7)
- m1 = massa van voorwerp 1 in kilogram
- m2 = massa van voorwerp 2 in kilogram
- r = afstand tussen de zwaartepunten van de voorwerpen.
 Afbeelding 2: schets met lijn door zwaartepunten
Afbeelding 2: schets met lijn door zwaartepuntenZwaartekracht en gravitatiekracht
De zwaartekracht die op de aarde uitgeoefend wordt is ook een gravitatiekracht. De aarde is dan m1, jij bent m2. Hoe kun je deze formule van de gravitatiekracht nu gebruiken om de zwaartekracht uit te rekenen?Fg = (G X m1 X m2) / r2
Afleiding van formule voor gravitatiekracht naar de zwaartekracht op aarde
Omdat op de aarde de zwaartekracht heerst mag je zeggen dat de zwaartekracht gelijk is aan de gravitatiekracht.Dus: Fzw= Fg
Aangezien de zwaartekracht op een massa m1 werkt die ook rechts van de formule voorkomt mag je deze massa's tegen elkaar wegstrepen. Streep m1 aan beide kanten weg.
m1 X g = (G X m1 X maarde)/r2
Je houdt nu in de vergelijking alleen de massa van de aarde over.
g = (G X maarde)/r2
Berekening zwaartekracht
Als je de zwaartekracht die op jou wordt uitgeoefend wil berekenen moet je de straal (r) gelijkstellen aan de afstand van jou tot aan het middelpunt van de aarde. Dit is dus weer die r.Rekenvoorbeeld berg in Tibet
Stel je staat in Tibet boven op een berg van 8 kilometer. Je wil weten wat de grootte van de valversnelling is die daar heerst. We gebruiken weer de formule voor de valversnelling.g = (G X maarde)/r2
BINAS tabel 31 geeft de massa en straal van planeten in ons zonnestelsel.
waarbij:
- straal aarde (r) = 6,378 . 106 meter
- massa aarde maarde = 5,976 . 1024 kilogram
g = (6,67.10 -11 X 5,976.1024)/(6,378 .106 + 8 .103)2= 9,77 ms-2
Dus de valversnelling boven op die berg is 9,77 ms-2. Je wil nu weten of de valversnelling dichter bij de kern van de aarde groter of kleiner is dan de waarde die je nu voor een hoogte van 8 kilometer hebt berekend. Je pakt je duikpak en gaat op weg naar de Marianentrog die 11 kilometer onder de oceaanbodem ligt.
Rekenvoorbeeld Marianentrog
De Marianentrog is een kloof in de zeebodem met een diepte van 11 kilometer. Wat is de waarde van de valversnelling daar?11 kilometer is 11.000 meter. Omdat de trog naar de aardkern toe ligt moet je die 11.000 meter van de straal van de aarde aftrekken.
g = (G X maarde)/r2
waarbij:
- straal aarde (r) = 6,378.106 meter.
- straal tot aan de Marianentrog is 6,378.106 meter – 11.000 meter = 6.367.000 meter = 6,367. 106 meter.
- massa aarde (maarde)= 5,976.1024 kilogram
Vul deze waardes in
g= (6,67.10-11 X 5,976.1024)/ (6,367.106)2 = 9,83 m s-2.
De valversnelling boven op die berg van 8 kilometer was 9,77 ms-2.
Dus de valversnelling onder in de Marianentrog is groter dan boven op de berg in Tibet.