Eenparige cirkelbeweging: bereken middelpuntzoekende kracht
Als een auto door de bocht gaat moet er een kracht op de wielen werken die ervoor zorgt dat hij niet uit de bocht vliegt. In dit geval is het de wrijvingskracht. Als de weg glad is, doordat er bijvoorbeeld olie op de weg ligt is er niet genoeg wrijvingskracht. Waarschijnlijk hou je onbewust rekening met deze wetenschap: je vermindert je snelheid. Wat is nu eigenlijk het verband tussen snelheid en middelpuntzoekende kracht?Wat is de middelpuntzoekende kracht?
De middelpuntzoekende kracht wordt ook wel de centripetale kracht genoemd. De naam “middelpuntzoekende kracht” verwijst naar het gevolg van die kracht. Bij een auto in de bocht zorgt de wrijvingskracht ervoor dat de auto de cirkelbaan blijft volgen. De wrijvingskracht veroorzaakt dus de middelpuntzoekende kracht. De middelpuntzoekende kracht werkt op een voorwerp dat in een eenparige cirkelbeweging beweegt.Grootte en richting van de middelpuntzoekende kracht
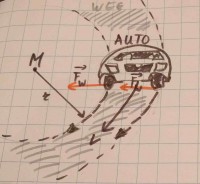Afbeelding 1: Fw zorgt hier voor de middelpuntzoekende krachtAndere voorbeelden van middelpuntzoekende kracht
Ook de zwaartekracht kan een middelpuntzoekende kracht veroorzaken. Door de zwaartekracht van de aarde draait de maan in een cirkelbaan rond de aarde. Bij het ronddraaien van een steen aan een touw wordt de middelpuntzoekende kracht veroorzaakt door het touw waarmee de steen wordt rondgeslingerd.De formule voor de middelpuntzoekende kracht
Fmpz = mv2/r in newton (N)
Waarbij:
- Fmpz = middelpuntzoekende kracht in newton (N)
- m = de massa in kilogram (kg)
- v = de snelheid in meter per seconde (ms-1)
- r = de baanstraal in meter (m)
Rekenvoorbeeld 1: auto met 50 kilometer per uur
Je auto met inzittenden weegt 980 kilogram. Je snelheid is 50 kilometer per uur. De straal van de bocht is 2 meter. Wat is je middelpuntzoekende kracht?Omrekenen naar meter per seconde
Reken eerst de snelheid om naar meter per seconde (ms-1).
Een uur is 60 minuten X 60 seconden = 3.600 seconden.
50 kilometer is 50 x 1000 meter = 50.000 meter.
50 km/hr = 50.000 meter/3600 seconden = 13,9 meter per seconde (ms-1).
Formule invullen
Fmpz = mv2/r
Waarbij:
- m (massa) = 980 kilogram
- v (snelheid) = 13,9 meter per seconde,
- r (straal) = 2 meter
Fmpz= 980 X (13,9)2/2 = 94.522 newton (N)
Dit is best wel een grote kracht die door de wrijving van je autobanden opgebracht moet worden. Stel je slipt in de bocht, maar het gaat net goed. Je vraagt je af, als je maar 30 kilometer per uur had gereden, wat dan de middelpuntzoekende kracht was geweest.
Rekenvoorbeeld 2: auto met 30 kilometer per uur
Je auto met inzittenden weegt 980 kilogram. Je snelheid is 30 kilometer per uur. De straal van de bocht is nog altijd 2 meter. Wat is je middelpuntzoekende kracht?Omrekenen naar meter per seconde
Een uur is 60 X 60= 3.600 seconden.
30 kilometer is 30 x 1000 = 30.000 meter.
30 km/hr = 30.000 meter/3600 seconden = 8,3 meter per seconde (ms-1).
Formule invullen
Fmpz = mv2/r
Waarbij:
- m (massa) = 980 kilogram,
- v(snelheid) = 8,3 meter per seconde,
- r(straal) = 2 meter
Fmpz = 980 X (8,3)2/2 = 34.028 newton (N)
Dus bij 50 kilometer per uur was Fmpz: 94.522 newton
Bij 30 kilometer per uur was Fmpz: 34.028 newton
De middelpuntzoekende kracht is bij 30 kilometer per uur maar ongeveer 1/3 van de middelpuntzoekende kracht bij 50 kilometer per uur. Je ziet dus dat het verlagen van je snelheid een grote impact heeft. Dit komt omdat bij de formule van middelpuntzoekende kracht de snelheid in het kwadraat meedoet. Vertrouw je het wegdek dus niet in een bocht: verminder je snelheid. Dan is de kans dat je uit de bocht vliegt kleiner!
Rekenvoorbeeld 3: wasgoed
Je hebt een wasmachine en je bent benieuwd welke krachten er bij het centrifugeren uitgeoefend worden. Het wasgoed in je wasmachine weegt 8 kilogram. De trommel van je wasmachine heeft een straal van 50 centimeter. Het toerental van het wasmachine is 1200 RPM (rounds per minute). Wat is de kracht die er op de trommel van je wasmachine tijdens het centrifugeren wordt uitgeoefend?Baansnelheid van de was uitrekenen
Wat is nu de snelheid (v)? 1200 RPM is 1200 ronden per minuut. 1 minuut is 60 seconden. Dus: 1200 RPM is 1200/60 = 20 omwentelingen per seconde.
Formule trillingstijd (of omwentelingstijd)
T = 1/f
waarbij f = 20 omwentelingen per seconde. '
Formule trillingstijd invullen
T= 1/20 = 0,05 seconden
Afgelegde weg uitrekenen
Formule afgelegde weg
Afgelegde weg (s) = 2 π r x aantal omwentelingen
waarbij:
r = 0,5 meter
π = 3.14
aantal omwentelingen = 20
Formule afgelegde weg invullen
Afgelegde weg (s) = 2 π r x aantal omwentelingen
s = 2 X π X r X 20 = 3.14 meter X 20 = 62,8 meter
Als het goed is zit er op je rekenmachine een knop voor π (pi). Dan werk je met het niet afgeronde getal.
Formule baansnelheid
v baan = (2 π r)/T
Waarbij:
- r (straal) = 0,5 meter
- T (trillingstijd) = 0,05 seconden
Formule invullen
v baan = (2 π 0,5)/0,05 = 62,8 meter per seconde.
Dus na al dat rekenwerk komen we op een snelheid uit van 62,8 meter per seconde die de was in de wastrommel heeft.
Middelpuntzoekende kracht uitrekenen
De kracht die 8 kilogram wasgoed op je wastrommel uitoefent bij een toerental van 1200 omwentelingen per minuut is dan:
Fmpz = mv2/r
Waarbij:
- m = 8 kilogram (kg)
- r = 50 centimeter = 0,5 meter
- v = 62,8 meter per seconde
Fmpz = 8 X (62,8)2/0,5 = 63.166 newton (N).
Dus je wasgoed van 8 kilogram oefent een kracht van 63.166 newton uit bij een toerental van 1200 omwentelingen per minuut.
