Eenparige beweging: bereken snelheid en verplaatsing
 Als je wil weten hoe de beweging van een fietser eruitzag kun je gebruik maken van een stopwatch en een meetlint. Vaak zit er op je smartphone (of een app die je kunt downloaden) een stopwatch. Als de fietser wegfietst start je de stopwatch. Je hebt de fietser verteld dat je wil dat hij langs een rechte lijn met een constante (dezelfde) snelheid fietst. Zo een soort beweging heet een eenparige rechtlijnige beweging. Als de fietser arriveert bij het eindpunt stop je de stopwatch. Als het goed is heb je van tevoren de afstand bepaald die de fietser moet afleggen. Met de gemeten waarden kun je een (x,t)-diagram en een (v,t)-diagram maken. Nu kun je een aantal zaken uit deze diagrammen afleiden.
Als je wil weten hoe de beweging van een fietser eruitzag kun je gebruik maken van een stopwatch en een meetlint. Vaak zit er op je smartphone (of een app die je kunt downloaden) een stopwatch. Als de fietser wegfietst start je de stopwatch. Je hebt de fietser verteld dat je wil dat hij langs een rechte lijn met een constante (dezelfde) snelheid fietst. Zo een soort beweging heet een eenparige rechtlijnige beweging. Als de fietser arriveert bij het eindpunt stop je de stopwatch. Als het goed is heb je van tevoren de afstand bepaald die de fietser moet afleggen. Met de gemeten waarden kun je een (x,t)-diagram en een (v,t)-diagram maken. Nu kun je een aantal zaken uit deze diagrammen afleiden.
Formule gemiddelde snelheid
Je berekent de gemiddelde snelheid met:vgem= Δx/Δt
Waarbij:
- vgem= gemiddelde snelheid in meter per seconde (m/s)
- Δx = verplaatsing in meter (m)
- Δt = gebruikte tijd in seconden (s)
Rekenen met de formule voor de gemiddelde snelheid
Stel de fietser heeft een afstand van 2000 meter afgelegd in 6 minuten (6 x 60 = 360 seconden). Wat is dan de gemiddelde snelheid in meter per seconden (m/s)?vgem= Δx/Δt
Waarbij:
- Δx = verplaatsing in meter (m): hier 2000 meter
- Δt = gebruikte tijd in seconden (s): hier 360 seconden
Je kunt de snelheid ook berekenen in kilometer per uur (km/h: h staat voor hour = uur)
vgem= Δx/Δt
Waarbij:
- Δx = verplaatsing in kilometer (km): hier 2
- Δt = gebruikte tijd in uur(s): hier 6 minuten = 0,1 uur
(x,t)-diagram maken
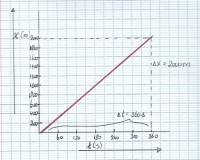 Afbeelding 1: het (x,t)-diagram
Afbeelding 1: het (x,t)-diagram- Zet op de horizontale as de tijd in seconden uit.
- Zet op de verticale as de afgelegde weg in meter uit.
- De fietser heeft na 0 seconden 0 meter afgelegd.
- De fietser heeft na 360 seconden bij het eindpunt 2000 meter afgelegd.
- Zet de (x,t)-punten in je diagram uit. Dus: eerste punt is (0,0) en tweede punt is (360, 2000).
- Trek met behulp van een liniaal een rechte lijn door deze 2 punten.
- Het resultaat is afbeelding 1: het (x,t)-diagram
Constante snelheid aflezen en berekenen
Afbeelding 1 geeft het (x,t)-diagram van de fietser tussen t = 0 en t = 360 seconden. In 360 seconden legt de fietser 2000 meter af. Je kunt met deze gegevens de gemiddelde snelheid berekenen:vgem= Δx/Δt
Waarbij:
- Δx = verplaatsing in meter (m): hier 2000 meter
- Δt = gebruikte tijd in seconden (s): hier 360 seconden
Iedere seconde fietst de fietser 6 meter. Voor elke periode tussen t = 0 seconden en t = 360 seconden wordt er per seconde 6 meter afgelegd. We zeggen dan dat de fietser met een constante snelheid fietst. We zeggen dan in plaats van: vgem = 6 m/s v= 6 m/s
Eenparige rechtlijnige beweging of eenparige beweging
Als de fietser langs een rechte lijn fietst en daarbij met steeds dezelfde snelheid (constante snelheid) noemen we dit een eenparige rechtlijnige beweging. Rechtlijnig slaat op de beweging langs de rechte lijn en eenparig slaat op de constante snelheid. Heel vaak wordt een eenparige rechtlijnige beweging een eenparige beweging genoemd.Steilheid van het (x,t)-diagram
Je ziet in afbeelding 1 dat het (x,t)-diagram een rechte lijn is. Dit heeft ermee te maken dat iedere periode (iedere seconde) de plaats (x) steeds met dezelfde hoeveelheid verandert (toeneemt). Dus de lijn van het diagram loopt overal even schuin. We zeggen dan dat het diagram overal net zo steil is. In afbeelding 1 kun je aflezen dat de plaats op t = 60 seconden 360 meter is. Op t = 240 seconden is de plaats x = 1440 meter. De steilheid van het (x,t)-diagram is dan gelijk aan:Vul in: Δx/Δt= (1440-360) m/(240-60) s = 6 m/s. De snelheid die we uit het diagram halen geeft de steilheid van het (x,t)-diagram aan.
Het (v,t)-diagram
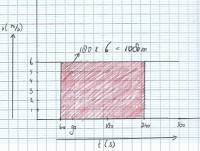 Afbeelding 2: het (v,t)-diagram van de fietser
Afbeelding 2: het (v,t)-diagram van de fietserVerplaatsing bepalen met de oppervlaktemethode
Je kunt uit een (v,t)-diagram ook de verplaatsing bepalen. Hiervoor gebruik je een berekening die ze de oppervlaktemethode noemen. Kijk naar afbeelding 2. Daar zie je verticaal tussen t = 60 seconden en t= 240 seconden een rood gebied gearceerd. Horizontaal wordt het rode gebied begrensd door v = 6 m/s. Als je nu het oppervlak van dit rood gebied berekend weet je de afgelegde weg.Dit doe je als volgt: s = v x t
Waarbij:
- s in meter is de verplaatsing:
- v in meter per seconde is de snelheid: hier 6 m/s
Vul in: s = v x t : 6 x 180 = 1080 meter
© 2019 - 2025 Blackbeauty, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Hoe bereken je snelheid en plaats met het (x,t)-diagram?Als een fietser vanuit stilstand optrekt en steeds harder gaat rijden kun je er niet meer van uitgaan dat de snelheid op…
Hoe bereken je snelheid en plaats met het (x,t)-diagram?Als een fietser vanuit stilstand optrekt en steeds harder gaat rijden kun je er niet meer van uitgaan dat de snelheid op…
 Versnelling en vertraging berekenen met het (v,t)-diagramAls een fietser vanuit stilstand wegfietst kun je zien dat zijn snelheid steeds groter wordt. Onze fietser begint op t =…
Versnelling en vertraging berekenen met het (v,t)-diagramAls een fietser vanuit stilstand wegfietst kun je zien dat zijn snelheid steeds groter wordt. Onze fietser begint op t =…
 (Snelheid,tijd)-diagram maken met (plaats,tijd)-diagramAls je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je hieruit het (snelheid,tijd)-diagram afleide…
(Snelheid,tijd)-diagram maken met (plaats,tijd)-diagramAls je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je hieruit het (snelheid,tijd)-diagram afleide…
 Afgelegde afstand aflezen met oppervlaktemethodeAls je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je uit dit diagram rechtstreeks aflezen wat de…
Afgelegde afstand aflezen met oppervlaktemethodeAls je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je uit dit diagram rechtstreeks aflezen wat de…
 Minimale lengte van startbaan voor een vliegtuig berekenenOp een vliegveld zie je dat vliegtuigen vanuit stilstand eerst enige tijd moeten versnellen om opstijgen mogelijk te mak…
Minimale lengte van startbaan voor een vliegtuig berekenenOp een vliegveld zie je dat vliegtuigen vanuit stilstand eerst enige tijd moeten versnellen om opstijgen mogelijk te mak…
 Het atoommodel van BohrNiels Bohr leverde een inmense bijdrage aan de natuurkunde. In 1913 kwam hij met een theorie voor het atoommodel, waarin…
Het atoommodel van BohrNiels Bohr leverde een inmense bijdrage aan de natuurkunde. In 1913 kwam hij met een theorie voor het atoommodel, waarin…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Skitterphoto, Pixabay
Blackbeauty (100 artikelen)
Laatste update: 05-05-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 1
Laatste update: 05-05-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.