Minimale lengte van startbaan voor een vliegtuig berekenen
Op een vliegveld zie je dat vliegtuigen vanuit stilstand eerst enige tijd moeten versnellen om opstijgen mogelijk te maken. Kleinere vliegtuigen hebben over het algemeen een kortere startbaan nodig. Daar maken ze op kleine vliegvelden handig gebruik van. Maar hoe kun je bepalen of de startbaan bij een vliegveld in de rimboe lang genoeg is voor je eigen (propeller)vliegtuig? Je moet in ieder geval weten wat de opstijgsnelheid en de versnelling van je vervoersmiddel is.Opstijgsnelheid en versnelling van je vliegtuig
Een Cessna 150 (propellervliegtuig) kan met een snelheid van 100 km/h opstijgen. De snelheid van dit type vliegtuig wordt iedere seconde vermeerdert met 2 m/s. De versnelling is dan 2 m/s2. Hoe lang moet de startbaan minimaal zijn om dit type vliegtuig op te laten stijgen?Omrekenen van de opstijgsnelheid naar meter per seconde
Reken eerst de snelheid in kilometer per uur (km/h) om naar meter per seconde (m/s).100 km/h = (100.000 meter)/(60 minuten x 60 seconden) = 100.000 m /3600 s = 27,8 m/s
Minimaal benodigde tijd om op te stijgen
Je kunt de formule van de versnelling gebruiken om de minimaal benodigde tijd om de juiste snelheid te verkrijgen berekenen. We willen een uitkomst in hele seconden en ronden voor de zekerheid naar boven af. Het is namelijk gevaarlijk als de snelheid net niet groot genoeg is. Dan worden er voor de zekerheid een aantal meters extra aan de startbaan geplakt!v gewenst = 27,8 m/s
a = 2 m/s2
a = Δv/Δt
2 = (veind – vbegin)/ Δt
2 = ((27,8 -0))/ Δt: kruiselings vermenigvuldigen.
Δt = ((27,8 -0))/2 = 14 seconden
Vervolgens kun je door het tekenen van het (v,t)-diagram de afgelegde weg en dus de minimaal benodigde lengte van de startbaan berekenen.
Maak het (v,t)-diagram
Dit diagram maak je door op de horizontale as de tijd uit te zetten (minimaal 14 seconden) en verticaal de snelheid in meter per seconde (maximaal 28 m/s). Omdat de versnelling over het hele tijdvak van 0 tot 14 seconden constant is wordt de grafiek een schuine rechte lijn. Start linksonder in de oorsprong (0,0). Dit komt overeen met een tijdstip t = 0 seconden en een snelheid van 0 m/s. Vervolgens mag je al het punt (14,28) gebruiken. Dit staat voor tijdstip t = 14 seconden en een snelheid van 28 m/s. Dit komt overeen met een snelheid rond de 100 kilometer per uur die de Cessna 150 (het propellervliegtuig) moet hebben om veilig te kunnen opstijgen. Als je een rechte lijn door deze twee punten trekt krijg je vervolgens het bijbehorende (v,t)-diagram. Met behulp van de oppervlaktemethode kun je nu de afgelegde weg berekenen.Berekenen van de afstand met de oppervlaktemethode
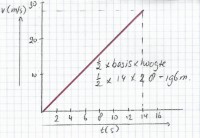Afbeelding 1: (v,t)-diagramBerekening met een lagere versnelling
Stel dat de Cessna 150 zeer zwaar beladen is en daardoor een lagere versnelling heeft. De versnelling is nu 1 m/s2. De gewenste snelheid blijft 100 kilometer per uur, wat overeenkomt met 27,8 meter per seconde. Hoe lang moet de startbaan nu minimaal zijn?vgewenst = 27,8 m/s
a = 1 m/s2
a = Δv/Δt
1 = (veind – vbegin)/ Δt
1 = ((27,8 -0))/ Δt: Kruiselings vermenigvuldigen.
Δt= ((27,8 -0))/1 = 27,8 seconden
Maak het (v,t)-diagram
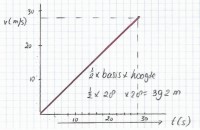Afbeelding 2: (v,t)-diagram met lagere versnelling
