Versnelling en vertraging berekenen met het (v,t)-diagram
Als een fietser vanuit stilstand wegfietst kun je zien dat zijn snelheid steeds groter wordt. Onze fietser begint op t = 0 seconden te fietsen. Na 10 seconden heeft hij een snelheid van 5 m/s. Als je het (v,t)-diagram tekent kun je vervolgens zijn versnelling berekenen. Een andere naam voor het (v,t)-diagram is het (snelheid,tijd)-diagram. Is de versnelling constant (eenparig versneld) dan mag je de snijlijnmethode gebruiken. De snelheid van de fietser neemt iedere seconde met dezelfde hoeveelheid toe of af. Verandert de versnelling voortdurend dan dien je de raaklijnmethode te gebruiken.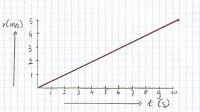 Afbeelding 1: (v,t)-diagram van t = 0 tot t = 10 seconden
Afbeelding 1: (v,t)-diagram van t = 0 tot t = 10 secondenHet (v,t)-diagram tekenen
Het (v,t)-diagram dat bij deze situatieschets hoort kun je vervolgens tekenen. Horizontaal zet je de tijd in seconden (s) uit. Daar je het hebt over een tijdsbestek van t = 0 tot t = 10 seconden laat je de horizontale as van 0 tot 10 seconden lopen. Verticaal zet je de snelheid in m/s uit. Daar de maximale snelheid hier 5 m/s wordt loopt de verticale as van 0 tot 5 m/s. In afbeelding 1 zie je het (v,t)-diagram van de eerste 10 seconden van de fietser.Snijlijnmethode en raaklijnmethode
Onze fietser fietst iedere seconde 0,5 m/s sneller. Dan is de versnelling 0,5 m/s per s, dus 0,5 m/s2. Als je de versnelling niet weet kun je deze berekenen door in het (v,t)-diagram de steilheid te bepalen. Als de versnelling niet overal hetzelfde is moet je op een aantal tijdstippen een raaklijn aan het (v,t)-diagram tekenen. Dit heet de raaklijnmethode. Dan krijg je de versnelling op dat tijdstip. Dat je de raaklijn gebruikt zie je rechts onderaan de haken: a = (Δv / Δt)raaklijn. Als je weet dat de versnelling (of vertraging) over het tijdsinterval overal hetzelfde is mag je gebruik maken van de snijlijnmethode. Je trekt dan een rechte lijn tussen het punt dat bij het begin hoort en het punt dat bij het einde hoort. Vervolgens bereken je de gemiddelde versnelling door a = (Δv / Δt)snijlijn.De formule voor de versnelling luidt:
a = Δv / Δt
Waarbij:
- a = versnelling in m/s2
- Δv = verschil tussen begin- en eindsnelheid: Δv = veind - vbegin
- Δt = verstreken tijd: Δt = teind - tbegin
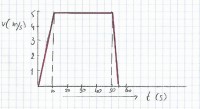 Afbeelding 2: (v,t)-diagram van t = 0 tot t = 55 seconden van eenparige versnelling en vertraging
Afbeelding 2: (v,t)-diagram van t = 0 tot t = 55 seconden van eenparige versnelling en vertragingHet (v,t)-diagram
Van t = 0 tot t = 10 seconden
De lijn heeft over de periode van 0 tot 10 seconden dezelfde steilheid. Je mag hier dan gebruik maken van de snijlijnmethode. In afbeelding 1 zag je dat de versnelling overal hetzelfde is. De versnelling is dan:a = (Δv / Δt)snijlijn = (5 – 0) m/s / (10-0) s = 0,5 m/s2
Van t = 10 tot t = 50 seconden
Na t = 10 seconden blijft de fietser met dezelfde snelheid doorfietsen. De lijn loopt dan horizontaal en de snelheid blijft tot t = 50 seconden 5 m/s.Van t = 50 tot t = 55 seconden
Op tijdstip t = 50 seconden remt onze fietser gelijkmatig en na 5 seconden is de snelheid veranderd van 5 m/s naar 0 m/s. Zie het (v,t)-diagram van afbeelding 2. De fietser remt gelijkmatig af. De snelheid neemt dan iedere seconde gelijkmatig af. Dit heet een eenparig vertraagde beweging. De vertraging kun je ook met het (v,t)-diagram van de beweging berekenen. Omdat de vertraging gelijkmatig is mag je weer gebruik maken van de snijlijnmethode. Je trekt een rechte (dalende) lijn tussen t = 50 en t= 55 seconden. De versnelling bereken je dan met:a = Δv / Δt
Waarbij:
- a = versnelling in m/s2
- Δv = verschil tussen begin- en eindsnelheid: Δv = veind - vbegin
- Δt = verstreken tijd: Δt = teind - tbegin
Bij afbeelding 2 luidt de versnelling:
a = Δv / Δt = (0-5) m/s / (55-50) s = -1 m/s2
De versnelling is -1 m/s2. Dit omdat de snelheid van de fietser steeds lager wordt. Je mag ook zeggen dat de vertraging 1 m/s2 is.
 Afbeelding 3: (v,t)-diagram met raaklijn
Afbeelding 3: (v,t)-diagram met raaklijnGeen gelijkmatige versnelling of vertraging
Stel nu dat onze fietser niet gelijkmatig was vertraagd. Dan had het (v,t)-diagram er anders uitgezien.Van t = 50 tot t = 51 seconden
We stellen nu dat onze fietser tussen t = 50 seconden en t = 51 seconden hard remt. Zijn snelheid gaat in een keer van 5 m/s naar 2 m/s. Dus zijn versnelling was:a = Δv / Δt = (2 – 5) m/s / (51-50) s = -3 m/s2. Je mag ook zeggen: de vertraging was 3 m/s2. Zie de raaklijn in afbeelding 3. Deze wordt aan de rode lijn en dan in de knik getrokken. Als je de raaklijn naar beneden doortrekt snijdt deze met de t-as op t = 51,7 seconden. Aan de rechterkant van afbeelding 3 staat het groene driehoekje uitvergroot. De schuine zijde is de raaklijn, verticaal is het snelheidsverschil (-5 m/s) en horizontaal is het tijdsverschil (van 50 seconden tot 51,7 seconde: 1,7 seconden). Er komt een waarde van -2,9 m/s2 uit. Dit benadert de berekende vertraging. Het feit dat de raaklijn met de hand is getekend verklaart waarschijnlijk de afwijking ten opzichte van de berekende waarde.