Hoe bereken je snelheid en plaats met het (x,t)-diagram?
 Als een fietser vanuit stilstand optrekt en steeds harder gaat rijden kun je er niet meer van uitgaan dat de snelheid op ieder tijdstip hetzelfde is. De snelheid in het begin is veel lager dan op het tijdstip dat de fietser zijn optimale snelheid heeft bereikt. Gelukkig kun je door gebruik te maken van het (plaats, tijd)-diagram of ook wel (x,t)-diagram de gemiddelde snelheid met een snijlijn bepalen. Als je wil weten wat de snelheid op een bepaald tijdstip is kun je de raaklijn gebruiken. Dit heet de raaklijnmethode.
Als een fietser vanuit stilstand optrekt en steeds harder gaat rijden kun je er niet meer van uitgaan dat de snelheid op ieder tijdstip hetzelfde is. De snelheid in het begin is veel lager dan op het tijdstip dat de fietser zijn optimale snelheid heeft bereikt. Gelukkig kun je door gebruik te maken van het (plaats, tijd)-diagram of ook wel (x,t)-diagram de gemiddelde snelheid met een snijlijn bepalen. Als je wil weten wat de snelheid op een bepaald tijdstip is kun je de raaklijn gebruiken. Dit heet de raaklijnmethode.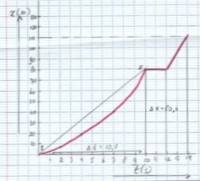 Afbeelding1: het (plaats,tijd)-diagram ofwel (x,t)-diagram
Afbeelding1: het (plaats,tijd)-diagram ofwel (x,t)-diagramHet (plaats, tijd)-diagram ofwel (x,t)-diagram
Als je wilt weten op welke plaats de fietser zich op een bepaald tijdstip bevindt kun je gebruik maken van het (x,t)-diagram. De x geeft dan de plaats aan en de t het tijdstip in seconden. In afbeelding 1 zie je het (x,t)-diagram van een fietser. In het begin (op t = 0) staat de fietser stil. Daarna probeert de fietser steeds sneller te fietsen. Na 10 seconden is de fietser moe. Tussen t = 10 en t = 12 seconden staat de fietser stil. Dit kun je zien aan het feit dat het (x,t)-diagram horizontaal loopt. Vanaf t = 12 seconden gaat de fietser hij met een constante snelheid fietsen. Dit kun je aflezen uit het (x,t)-diagram. Vanaf t = 0 tot t = 10 seconden zie je dat de grafiek steeds steiler gaat lopen. Vanaf t = 10 seconden loopt de grafiek horizontaal tot t =12 seconden. Gedurende deze 2 seconden staat de fietser stil. Na t = 12 seconden blijft de grafiek overal net zo steil lopen: de snelheid is nu constant. Om de gemiddelde snelheid over een periode te berekenen kun je gebruik maken van een snijlijn. Wil je de snelheid op een tijdstip berekenen, dan kun je gebruik maken van de raaklijn op dat tijdstip aan de grafiek.Gemiddelde snelheid bepalen met de snijlijn
Een fietser die deelneemt aan een tijdrit begint op t = 0 te fietsen. Na 10 seconden heeft hij 80 meter gefietst.Gemiddelde snelheid ruwweg berekenen
Met een ruwe berekening kun je de gemiddelde snelheid berekenen.vgem = Δx/Δt
Waarbij:
- Δx = verplaatsing in meter (m): hier 80 meter
- Δt = gebruikte tijd in seconden (s): hier 10 seconden
Vul in: vgem = Δx/Δt = 80,0/10,0 = 8,0 m/s.
Gemiddelde snelheid met snijlijn berekenen
Tijdstip van t = 0 tot t = 10 secondenIn afbeelding 1 staat het (x,t)-diagram van de beweging van de fietser weergegeven. De lijn die van I tot II loopt heet de snijlijn. Je kunt de gemiddelde snelheid van de fietser berekenen met behulp van de snijlijn. De gemiddelde snelheid van de fietser is dan gelijk aan de steilheid van de snijlijn. De berekening is als volgt: vgem = Δx/Δt van de snijlijn: vgem = (80,0-0)/(10,0-0) = 8,0 m/s. De snelheid van de fietser is in het stuk van 0 tot 4 seconden lager dan in het stuk van 4 seconden tot 10 seconden.
Tijdstip van t = 0 tot t = 4 seconden
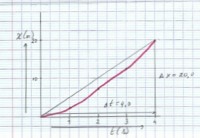 Afbeelding 2: het (x,t)-diagram t= 0 tot t=4
Afbeelding 2: het (x,t)-diagram t= 0 tot t=4vgem = Δx/Δt van de snijlijn
Vul in: vgem = (20,0-0)/(4,0-0) = 5,0 m/s. De steilheid in de tijdspanne van 0 tot 4 seconden is kleiner dan in het stuk van 6 tot 10 seconden. In het eerste stuk is de gemiddelde snelheid 5,0 m/s, in het laatste stuk is de snelheid groter dan 5,0 m/s en ook groter dan 8,0 m/s.
Snelheid op een tijdstip bepalen met de raaklijn: raaklijnmethode
Uit afbeeldingen 1 en 2 kun je afleiden dat de snelheid op het laatste stuk (tussen t = 6 en t = 10 seconden) hoger is dan 8,0 m/s. Dat kun je zien omdat het (x,t)-diagram steeds steiler gaat lopen. Als je nu wil weten wat de snelheid op een exact moment is kun je gebruik maken van een raaklijn. Dus de snelheid op een tijdstip kun je verkrijgen door een raaklijn te gebruiken.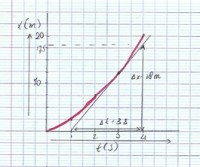 Afbeelding 3: raaklijn bij t = 3 seconden
Afbeelding 3: raaklijn bij t = 3 secondenBerekening raaklijnmethode
Bij afbeelding 3 zie je dat er een raaklijn getekend is bij t = 3 seconden. Met behulp van de steilheid van de raaklijn kun je berekenen wat de snelheid op t = 3 seconden is. Dit noemen we de raaklijnmethode. Let op: de gemiddelde snelheid kun je berekenen met de snijlijn. De snijlijn gaat door 2 punten, de raaklijn raakt in 1 punt aan de lijn in het diagram.v = Δx/Δt van de raaklijn: v = (18,0-0)/(4,0-1,0) = 4,5 m/s