(Snelheid,tijd)-diagram maken met (plaats,tijd)-diagram

Als je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je hieruit het (snelheid,tijd)-diagram afleiden. Dit kun je doen door op een aantal tijdstippen de snelheid te bepalen met de raaklijnmethode. Met deze waardes voor de snelheid kun je dan het (snelheid,tijd)-diagram tekenen. Een andere naam voor het (plaats,tijd)-diagram is het (x,t)-diagram. Een andere aanduiding voor het (snelheid,tijd)-diagram is het (v,t)-diagram.

Raaklijnmethode en snijlijnmethode

Voor het tekenen van het (v,t)-diagram moet je officieel de raaklijnmethode gebruiken. Deze methode geeft de snelheid op een tijdstip weer. Als je ziet dat de lijn in het (x,t)-diagram tussen twee tijdstippen net zo steil blijft lopen kun je voor deze periode de gemiddelde snelheid met behulp van de snijlijnmethode uitrekenen. Hiermee bespaar je dan tijd omdat je dan niet voor ieder tijdstip de raaklijn hoeft te bepalen.

Tekenen van het (v,t)-diagram met behulp van de raaklijnmethode en de snijlijnmethode

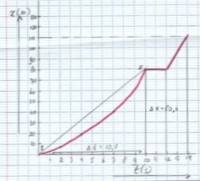Afbeelding1: het (plaats,tijd)-diagram ofwel (x,t)-diagram

Als je het (v,t)-diagram uit een (x,t)-diagram wil verkrijgen moet je op een aantal strategisch gekozen tijdstippen de raaklijn tekenen om de snelheid te bepalen. We nemen als voorbeeld een fietser die op het tijdstip t = 0 begint met optrekken.

Tussen t = 0 en t = 10 versnelt de fietser. De lijn in het (x,t)-diagram gaat steeds steiler lopen. Zie afbeelding 1: het (x,t)-diagram. Als de lijn in het (x,t)-diagram steeds steiler wordt betekent dit dat de snelheid van de fietser hoger wordt. Wil je op individuele punten (op een bepaald tijdstip) de snelheid weten moet je de raaklijnmethode gebruiken.

Snijlijnmethode

Als je de gemiddelde snelheid wil weten moet je de snijlijn tekenen en dan de gemiddelde snelheid uitrekenen. Met behulp van het (x,t)-diagram kun je op een eenvoudige manier aflezen dat tussen t = 0 en t = 10 seconden de gemiddelde snelheid 8,0 m/s is. De fietser die deelneemt aan een tijdrit begint op t = 0 te fietsen. Na 10 seconden heeft hij 80 meter gefietst. De snijlijn is de schuine lijn die door I en II wordt aangegeven. Dan is de gemiddelde snelheid dus (80-0) m /(10-0) s = 8,0 m/s. Je ziet echter wel dat de lijn van de grafiek steeds steiler gaat lopen. De snelheid tussen t = 0 en t = 8 seconden is dus niet overal hetzelfde: je zult een aantal raaklijnen moeten tekenen om een (v,t)-diagram te kunnen tekenen.

Raaklijnmethode

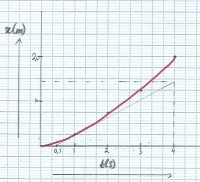Afbeelding 2: raaklijn bij t = 1 seconden

Als de lijn in het (x,t)-diagram niet recht is, moet je op het gewenste tijdstip een raaklijn tekenen. Hoe dit moet kun je zien in afbeelding 2. Het tijdsinterval tussen t = 0 en t = 4 seconden is uitvergroot. In afbeelding 2 is op het tijdstip t = 1 een raaklijn aan de grafiek getekend. We verlengen de raaklijn zo ver als mogelijk en laten hem de horizontale as snijden. Dan hebben we een beginwaarde voor t = 0,5 seconden die we af kunnen lezen. We laten de raaklijn aan de rechterkant lopen tot t = 4 seconden. Voor de afgelegde weg is de beginwaarde bij t = 0,5 0 meter. Rechts bij t = 4 seconden kun je aflezen dat x = 14.5 meter. Maak het "driehoekje" zo groot als mogelijk zodat aflezen beter gaat. Nu kunnen we de snelheid op t = 1 seconden uitrekenen met:

v = Δx/Δt van de raaklijn: v = (14,5-0)/(4,0-0,5) = 4,1 m/s

Tussen t = 0 en t = 10 seconden

Als je dezelfde methode gebruikt voor t= 1 tot en met t = 10 krijg je de volgende waarden:
t = 0: 0 m/s; t = 2: 6 m/s; t = 3: 6,3 m/s; t= 4: 6 m/s
t = 5: 7 m/s; t = 7: 7,5 m/s; t = 9: 11 m/s

Tussen t = 10 en t = 12 seconden

Omdat de lijn horizontaal loopt in het (x,t)-diagram van afbeelding 1 is er tussen t = 10 en t =12 geen verplaatsing. De fietser staat dus stil. In het (v,t)-diagram is de snelheid dan 0 m/s.

Tussen t = 12 en t = 14 seconden

Tussen t = 12 seconden en t =14 seconden heeft de fietser een constante snelheid. Deze kun je dan berekenen met (snijlijnmethode): Vgem = Δx/Δt = (110,0-80,0)/(14,0-10,0) = 7,5 m/s.

Het tekenen van het (v,t)-diagram

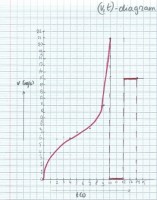Afbeelding 3: het (v,t)-diagram

Nu je de snelheid op een groot aantal tijdstippen hebt bepaald kun je het (v,t)-diagram tekenen. Horizontaal geef je de tijd in seconden aan, verticaal de snelheid in m/s.

Als je het (v,t)-diagram bekijkt vallen er een aantal zaken op:

Tot t = 10 seconden neemt de snelheid toe: daarna is de snelheid ineens 0 m/s: de fietser is abrupt gestopt.
Tussen t= 10 en t= 12 seconden is de lijn horizontaal en zit ter hoogte van de t-as. De fietser heeft een snelheid van 0 m/s: hij staat stil.
Tussen t =12 en t = 14 seconden is de lijn horizontaal: de snelheid van de fietser constant: 15 m/s.