Afgelegde afstand aflezen met oppervlaktemethode
Als je een beweging al beschreven hebt met een (plaats,tijd)-diagram, kun je uit dit diagram rechtstreeks aflezen wat de afgelegde afstand is. Als je alleen het (snelheid,tijd)-diagram tot je beschikking hebt kun je met behulp van de oppervlaktemethode berekenen wat de afgelegde afstand was. Een (plaats,tijd)-diagram wordt ook met (x,t)-diagram aangeduid. Een (snelheid,tijd)-diagram wordt ook met (v,t)-diagram aangeduid.Beschrijving van de beweging van de fietser
Een fietser begint op t = 0 seconden te fietsen. Hij trekt op en rijdt na 10 seconden met een constante snelheid van 5 m/s. Na 90 seconden ziet hij in de verte zijn einddoel. Dan begint hij af te remmen. Na 100 seconden staat hij stil, precies op het eindpunt. Je kunt de afgelegde weg aflezen uit het (x,t)-diagram of berekenen met het (v,t)-diagramHet (x,t)-diagram tekenen
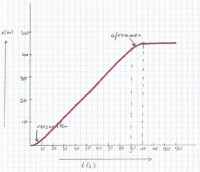Afbeelding 1: (x,t)-diagramAfgelegde weg aflezen in het (x,t)-diagram
In het (x,t)-diagram kun je aflezen dat de fietser bij t = 100 seconden (het eindpunt) 450 meter heeft afgelegd. Na t = 100 seconden (en tot t = 130 s) staat de fietser stil. Dit kun je in het het (x,t)-diagram zien aan het feit dat de lijn horizontaal loopt en horizontaal blijft doorlopen tot t = 130 seconden. De afgelegde afstand blijft 450 meter.Het (v,t)-diagram tekenen
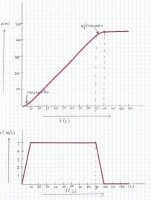Afbeelding 2: (x,t)-diagram boven en (v,t)-diagram onderTussen t = 0 en t = 10 seconden
Tussen t = 0 en t = 10 seconden trekt de fietser op. Er is gegeven dat op t = 10 seconden de fietser een snelheid heeft van 5 m/s. Op t = 0 seconden had de fietser een snelheid van 0 m/s. We stellen voor deze situatie dat de versnelling van de fietser op het stuk tussen t = 0 en t = 10 seconden overal hetzelfde was. Trek een rechte lijn tussen punt (0,0) en (10,5) waarbij (10,5) in het (v,t)-diagram t = 10 seconden en v = 5 m/s voorstelt. Deze lijn is schuin en stijgend.Tussen t = 10 en t = 90 seconden
Tussen t = 10 en t = 90 seconden is de snelheid constant. Gegeven is dat deze 5 m/s is. Dat de snelheid hetzelfde blijft in dit tijdsvak kun je zien aan het feit dat de lijn horizontaal blijft lopen.Tussen t = 90 en t = 100 seconden
Tussen t = 90 en t= 100 seconden remt de fietser af. We gaan er weer van uit dat de vertraging in het tijdvak tussen t = 90 en t= 100 seconden overal hetzelfde is. Je kunt nu een schuine rechte lijn naar beneden tekenen. Begin bij t = 90 seconden (90,5) en trek de lijn naar beneden naar (100,0) bij t = 100 seconden.Tussen t = 100 en t = 130 seconden
Na 100 seconden blijft de fietser stil staan. Zijn snelheid is 0 m/s. Dit zie je aan het (v,t)-diagram doordat de lijn ter hoogte van de t-as verder loopt.Afgelegde weg berekenen met de oppervlaktemethode
Als je de oppervlakte onder het (v,t)-diagram wil berekenen ga je als volgt te werk:Van t= 0 tot t= 10 seconden
Dit is een driehoek. De oppervlakte van een driehoek reken je uit met een half maal basis maal hoogte: 0,5 x t x v = 0,5 x 10 seconden x 5 m/s = 25 m.Van t = 10 tot t = 90 seconden
Dit is een rechthoek. De oppervlakte van een rechthoek reken je uit door basis maal hoogte te doen: t x v = (90-10) seconden x 5 m/s = 400 m.Van t = 90 seconden tot t = 100 seconden
Dit is weer een driehoek. De oppervlakte van een driehoek reken je uit met een half maal basis maal hoogte: 0,5 x t x v = 0,5 x (100-90) seconden x 5 = 25 m.In totaal is de afgelegde afstand dus: 25 m + 400 m + 25 m = 450 m. Dit is dezelfde waarde als die we afgelezen hebben uit het (x,t)-diagram.
