Het Butterfly-effect gedemonstreerd in Excel
 Het butterfly-effect is een metafoor die voor het eerst gebruikt werd bij het voorspellen van het weer. De term werd geïntroduceerd door Edward Lorenz, een Amerikaans wiskundige en meteoroloog aan het Massachusetts Institute of Technology tijdens een lezing met de titel 'Veroorzaakt een vleugelslag van een vlinder in Brazilië een tornado in Texas?' Hiermee wordt bedoeld dat het zeer kleine effect van de slag van de vleugel van de vlinder op de atmosfeer in Brazilië in een domino-effect de atmosfeer in Texas zo verandert dat de condities in die atmosfeer een tornado veroorzaken. Het vlinder-effect speelt een belangrijke rol in de Chaostheorie. Chaotische systemen zijn buitengewoon afhankelijk van kleine verschillen in de begincondities.
Het butterfly-effect is een metafoor die voor het eerst gebruikt werd bij het voorspellen van het weer. De term werd geïntroduceerd door Edward Lorenz, een Amerikaans wiskundige en meteoroloog aan het Massachusetts Institute of Technology tijdens een lezing met de titel 'Veroorzaakt een vleugelslag van een vlinder in Brazilië een tornado in Texas?' Hiermee wordt bedoeld dat het zeer kleine effect van de slag van de vleugel van de vlinder op de atmosfeer in Brazilië in een domino-effect de atmosfeer in Texas zo verandert dat de condities in die atmosfeer een tornado veroorzaken. Het vlinder-effect speelt een belangrijke rol in de Chaostheorie. Chaotische systemen zijn buitengewoon afhankelijk van kleine verschillen in de begincondities.
Het weer van Edward Lorenz
Lorenz was in de eerste plaats een wiskundige die zich door omstandigheden met het weer ging bezig houden. Hij deed dat met behulp van een door hem zelf ontworpen weersysteem. Bron: Bob Fleischer, Wikimedia Commons (CC BY-2.0)
Bron: Bob Fleischer, Wikimedia Commons (CC BY-2.0)Lorenz gebruikte de Royal-McBee LGP-30 computer om een eigen weersysteem te programmeren. Het was de eerste draagbare computer van bijna 400 kg(!) die erg populair was onder wetenschappers. De machine produceerde iedere minuut een dag weer met behulp van 12 vergelijkingen, die verbanden tussen temperatuur en luchtdruk en verbanden tussen luchtdruk, windsnelheid en windrichting vastlegden. Lorentz bestudeerde de cycli van wind en temperatuur. De winden en temperaturen in dit eenvoudige systeem veranderden volgens een bepaald patroon, dat nooit precies hetzelfde was. Dat laatste was een niet geringe prestatie. Door deze niet-repeterende periodiciteit werd het op het instituut waar hij werkte een sport om aan de hand van de uitdraaien 'het weer van Lorentz' te voorspellen.
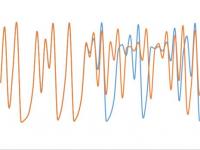 Illustratie van afwijkingen in een patroon
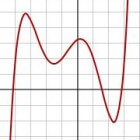
Illustratie van afwijkingen in een patroonOp een dag wilde hij deze patronen over een langere periode bestuderen. Normaal gesproken betekende dat dat hij de computer opnieuw zou opstarten, maar nu besloot hij ergens halverwege te beginnen. Dus voerde hij aan de hand van een eerdere uitdraai de getallen in en startte zijn weer met deze gegevens op. Na een uur bleken de resultaten zeer verrassend. In plaats van dat het weer zich exact op dezelfde manier ontwikkelde als eerder, bleken er afwijkingen op te treden in een tempo waarbij uiteindelijk elke gelijkenis met de vorige uitdraai verdwenen was. In de afbeelding 'Illustratie van afwijkingen in een patroon' is te zien dat de blauwe en rode lijn in het begin samenvallen, maar uiteindelijk steeds meer van elkaar afwijken.
Verklaring van de afwijkingen
Lorentz dacht eerst dat er iets mis was met de computer, dat één van de vacuümbuizen niet in orde was, tot hij zich realiseerde dat het aan iets heel anders lag. Bij het overtypen van de gegevens had hij gebruik gemaakt van afgeronde getallen, met de veronderstelling dat een afronding op duizendsten een te verwaarlozen verschil in de uitkomsten zou opleveren. Maar de computer rekende met zes cijfers achter de komma. Hij geeft het voorbeeld van de afgeronde waarde 0,506 die in de computer als 0,506127 was opgeslagen, een fout van ongeveer 0,025 %. Bij het meten van de factoren die het weer bepalen was de meetfout meestal een stuk groter. De wetenschappelijke intuïtie voorspelde dat al die kleine verschillen elkaar wel zouden opheffen voordat ze ook maar enige invloed op zo'n groot en complex systeem als het weer zouden krijgen. Het feit dat dat toch gebeurde, was een verrassing die Lorentz tot de conclusie bracht dat systemen die niet-periodiek gedrag vertoonden, zoals zijn eigen weer dat iedere dag weer anders was, onvoorspelbaar waren. Het zou uitmonden in de Chaos-theorie, een tak van de wiskunde die zich bezig houdt met dynamische systemen die sterk afhankelijk zijn van kleine verschillen in de begincondities.Demonstratie van het Butterfly-effect in Excel
In het werkblad wordt een iteratieve (herhalende) berekening uitgevoerd met gebruik van de formule zn+1 = 4zn(1-zn). De beginwaarden voor z zijn respectievelijk 0,40000000 en 0,40000001. In stap 1 wordt de uitkomst berekend van 4 x 0,4 x (1 - 0,4) = 0,96. In stap 2 wordt 0,96 in de formule ingevuld: 4 x 0,96 x (1 - 0,96) = 0,1536 enzovoort. De twee kolommen met uitkomsten voor respectievelijk 0,40000000 en 0,40000001 worden met elkaar vergeleken. Opgemaakte Werkblad
Opgemaakte WerkbladVoer de volgende stappen uit:
- Zet in A1, B1, C1, E1 en F1 respectievelijk "stap", "startwaarde 1", "startwaarde 2", "constante 1", "constante 2" (zonder de aanhalingstekens).
- Geef A2 de waarde 0 en A3 de waarde 1; selecteer de cellen A2 en A3, plaats de cursor op het kleine zwarte blokje rechts onder de geselecteerde cellen en trek met de linkermuisknop ingedrukt het blokje naar beneden tot A52.
- Selecteer de kolommen B en C door met de cursor op B te gaan staan, de linkermuisknop in te drukken en de muis vervolgens naar C te bewegen. Klik in het geselecteerde gebied met de rechtermuisknop en kies voor Celeigenschappen, Getal en zet het aantal decimalen op 8.
- Geef B2 de waarde 0,40000000 (0,4 met zeven nullen) en C2 de waarde 0,40000001 (0,4 met zes nullen en een 1)
- Geef E2 de waarde 4 en F2 de waarde 1
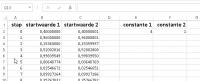 Werkblad met berekeningen
Werkblad met berekeningenEr wordt gebruik gemaakt van relatieve verwijzingen en absolute verwijzingen. Een voorbeeld van een relatieve verwijzing in C1 is "=A1+B1"; als de inhoud van C1 naar C2 wordt gekopieerd, staat in C2 "=A2+B2". Een absolute verwijzing in C1 zou zijn "=$A$1+$B$1". Na kopieren naar C2 staat dit er nog steeds.
- Zet in B3 "=$E$2*B2*($F$2-B2)" of kopieer de formule naar het werkblad zonder de aanhalingstekens
- Zet in C3 "=$E$2*C2*($F$2-C2)" of kopieer de formule naar het werkblad zonder de aanhalingstekens
- Selecteer B3 en C3, plaats de cursor op het kleine zwarte blokje rechts onder de geselecteerde cellen en trek met de linkermuisknop ingedrukt het blokje naar beneden tot B52.
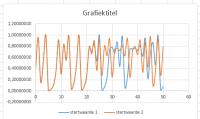 Grafiek Butterfly-effect in Excel
Grafiek Butterfly-effect in ExcelAan de uitkomsten in de twee kolommen is al te zien dat de waarden in het begin praktisch gelijk oplopen en vanaf stap 20 (als afgerond wordt op 2 cijfers achter de komma) van elkaar beginnen te verschillen. In een grafiek is dat in één oogopslag te zien.
- Selecteer Cel A1 tot en met cel C52
- Klik in het lint op "Invoegen" en bij "Grafieken" op het kleine zwarte pijltje naast "Spreidings-(X,Y) of bellendiagram invoegen" en klik op "Spreiding met vloeiende lijnen".
- Sla op als "Butterfly-effect.xlxs".
Door het document Butterfly-effect.xlxs te downloaden en te openen in Excel en vervolgens wat te spelen met de startwaarden en de constanten wordt duidelijk dat dit "chaotische systeem" slechts bij bepaalde waarden optreedt. In veel gevallen nadert de waarde voor beide kolommen op dezelfde manier naar 0 of een andere waarde. In een aantal gevallen schommelen beide waarden op dezelfde wijze rond een bepaald evenwichtspunt. Voorspelbaar en niet chaotisch.
 Bitcoinkoers in week 4 2018
Bitcoinkoers in week 4 2018 Het Butterfly-effect in de praktijk
Chaotische systemen zijn overal om ons heen te zien. Uiteraard het weer, maar ook bijvoorbeeld in het verkeer. Een auto die plotseling vaart vermindert, kan kilometers terug een enorme file veroorzaken. Het voorspellen van de bitcoinkoers is onmogelijk. Zelfs het vermoeden dat er ergens een regering is die de munt wil verbieden, kan tot een enorme waardedaling leiden.© 2018 - 2025 3s4u, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Een cursus Excel volgenExcel is een spreadsheetprogramma dat onderdeel uitmaakt van het pakket Windows MS Office. Excel wordt ook wel MS Excel…
Een cursus Excel volgenExcel is een spreadsheetprogramma dat onderdeel uitmaakt van het pakket Windows MS Office. Excel wordt ook wel MS Excel…
 Word: Brief samenvoegen met lijst in ExcelDe functie Afdruk samenvoegen in Word 2000 is heel gemakkelijk als je dezelfde brief wilt sturen naar verschillende mens…
Word: Brief samenvoegen met lijst in ExcelDe functie Afdruk samenvoegen in Word 2000 is heel gemakkelijk als je dezelfde brief wilt sturen naar verschillende mens…
 Excel: één werkblad voor talloze grafiekenIn Microsoft Excel zijn op eenvoudige wijze grafieken te maken. Door in het werkblad aan cellen de waarden van de coëffi…
Excel: één werkblad voor talloze grafiekenIn Microsoft Excel zijn op eenvoudige wijze grafieken te maken. Door in het werkblad aan cellen de waarden van de coëffi…
 Cursus: het aanbod van Excel-cursussenExcel is een programma dat veel gebruikt wordt. Het programma heeft veel mogelijkheden voor iemand die "iets" met cijfer…
Cursus: het aanbod van Excel-cursussenExcel is een programma dat veel gebruikt wordt. Het programma heeft veel mogelijkheden voor iemand die "iets" met cijfer…
 Een opwaartse ijspegel (stalagmiet) bij vriezend weerEen combinatie van oostenwind en lage temperaturen uit het oosten, doet water bevriezen. Water in slootjes, water in pla…
Een opwaartse ijspegel (stalagmiet) bij vriezend weerEen combinatie van oostenwind en lage temperaturen uit het oosten, doet water bevriezen. Water in slootjes, water in pla…
 De schaduw van de aarde en het blauwe en gouden uurtjeBij een heldere lucht kunnen we net voor de zon opkomt of net onder is gegaan, de schaduw van onze eigen aarde zien. In…
De schaduw van de aarde en het blauwe en gouden uurtjeBij een heldere lucht kunnen we net voor de zon opkomt of net onder is gegaan, de schaduw van onze eigen aarde zien. In…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Schwoaze, Pixabay
- James Gleick, "Chaos, making a new science", Open Road Integrated Media, 2011
- https://en.wikipedia.org/wiki/Butterfly_effect
- Afbeelding bron 1: Bob Fleischer, Wikimedia Commons (CC BY-2.0)
3s4u (17 artikelen)
Gepubliceerd: 29-01-2018
Rubriek: Wetenschap
Subrubriek: Weer
Bronnen en referenties: 4
Gepubliceerd: 29-01-2018
Rubriek: Wetenschap
Subrubriek: Weer
Bronnen en referenties: 4
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.