Gini-coëfficiënt en Gini-index
Wat is de Gini-coëfficiënt in de economie en waar wordt het voor gebruikt? Zitten er veel verschillen in de Gini-coëfficiënten van verschillende landen? Hoe kun je de Gini-coëfficiënt berekenen? Dit artikel geeft antwoorden op deze vragen. Ook al heeft u geen kennis van economie, dan kunt u toch deze informatie begrijpen. Deze informatie is ook geschikt voor studenten van de middelbare school.Gini-coëfficiënt
De Gini-coëfficiënt is een middel uit de economie om zeer gemakkelijk te kunnen zien wat de gelijkheid, of beter de ongelijkheid, van bepaalde situaties is. De Gini-coëfficiënt wordt weergegeven als een getal. Dit getal ligt tussen de 0 en de 1. Hoe kleiner het getal, dus hoe dichter het bij de 0 ligt, hoe gelijker het verschijnsel is. Hoe groter het getal, dus hoe dichter het bij de 1 ligt, hoe ongelijker het verschijnsel is. Als de Gini-coëfficiënt gelijk is aan 0, betekent dat dus een gelijkheid die niet gelijker kan. Bij het meten van de inkomensongelijkheid, waarbij vaak de Gini-coëfficiënt gebruikt wordt, betekent dat dat iedereen hetzelfde inkomen heeft. Als de Gini-coëfficiënt gelijk is aan 1, betekent dat dus een perfecte ongelijkheid. Bij het voorbeeld van het meten van de inkomensongelijkheid betekent dat dat één iemand al het inkomen heeft en de rest niets heeft.Gini-index
De Gini-index is niets anders dan de Gini-coëfficiënt uitgedrukt in een percentage. Een Gini-coëfficiënt van 1 komt overeen met 100%. Stel dat de Gini-coëfficiënt van de inkomensverdeling in een land 0,326 is, dan is de Gini-index van dat land 32,6% (dit was tevens de Gini-index van Nederland in 2004).Berekening Gini-coëfficiënt
De Gini-coëfficiënt is te berekenen door middel van de Lorenz-curve. De Lorenz-curve heeft eigenlijk twee gebieden onder de diagonaal. Het deel tussen de diagonaal en de curve: Deel 1. En het deel onder de curve: Deel 2. De Gini-coëfficiënt is de oppervlakte van deel 1 gedeeld door de oppervlakte van deel 1 en deel 2 opgeteld. De formules van de Gini-coëfficiënt en de Gini-index zijn dus:Gini-coëfficiënt = Opp. deel 1 / (Opp. deel 1 + Opp. deel 2)
Gini-index = Opp. deel 1 / (Opp. deel 1 + Opp. deel 2) x 100%
Toepassing
De Gini-coëfficiënt wordt bij veel situaties gebruikt. Vaak wordt het gebruikt bij de inkomensverdeling van een gebied of land. Maar elke ongelijkheid in vele situaties kunnen met de Gini-coëfficiënt verduidelijkt worden.De Gini-coëfficiënten van landen verschillen enorm. In 2004 stond Hongarije met een Gini-coëfficiënt van 0,244 op nummer 1 met de laagste Gini-coëfficiënt. Echter, Namibië had een Gini-coëfficiënt van 0,707. Enkele opvallende feiten:
De Scandinavische landen hebben altijd een erg lage Gini-coëfficiënt (rond de 0,25).
Veel Oost-Europese landen hebben een lage Gini-coëfficiënt. Vaak hebben (voormalig) communistische landen een lage Gini-coëfficiënt met uitzondering van bijvoorbeeld Rusland, wat opmerkelijk is.
Zuid-Amerikaanse landen en Afrikaanse landen hebben vaak een zeer hoge Gini-coëfficiënt. Namibië had in 2004 een Gini-coëfficiënt van 0,707. Dit komt waarschijnlijk doordat daar ontzettend rijke en ontzettend arme mensen wonen. Doordat de inkomens van die mensen niet genivelleerd worden, ontstaan er enorme verschillen. Ook speelt een rol dat het land erg corrupt is.
Corrado Gini
Corrado Gini was de bedenker van de Gini-coëfficiënt. Corrado Gini is geboren op 23 mei 1884 in het kleine dorpje Motta di Livenza in de buurt van Venetië, Italië. Hij studeerde wiskunde, economie en biologie aan een universiteit in Bologna. Zijn carrière was succesvol, mede dankzij het ontwikkelen van de Gini-coëfficiënt. Op 13 maart 1965 overleed hij.© 2010 - 2025 Jokaz, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
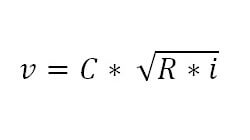 Formule van ChézyDe formule van Chézy is een formule die voortkomt uit de vloeistof leer. De zeer bekende formule is in 1775 ontwikkeld d…
Formule van ChézyDe formule van Chézy is een formule die voortkomt uit de vloeistof leer. De zeer bekende formule is in 1775 ontwikkeld d…
 Alcoholvrije cocktails voor kids en volwassenenJe geeft een feestje maar de mensen moeten daarna nog naar huis. Of er gaan een paar mensen BOB moeten spelen, of je kan…
Alcoholvrije cocktails voor kids en volwassenenJe geeft een feestje maar de mensen moeten daarna nog naar huis. Of er gaan een paar mensen BOB moeten spelen, of je kan…
 Uitwendige ballistiek: baan van de kogelUitwendige of externe ballistiek houdt zich bezig met het gedrag van een kogel nadat hij de loop heeft verlaten, maar vo…
Uitwendige ballistiek: baan van de kogelUitwendige of externe ballistiek houdt zich bezig met het gedrag van een kogel nadat hij de loop heeft verlaten, maar vo…
 Welvaart, markten en overheid (rechtseconomie)In dit artikel worden enkele kernbegrippen van de (rechts)economie beschreven. Daarnaast wordt er gekeken naar de verzek…
Welvaart, markten en overheid (rechtseconomie)In dit artikel worden enkele kernbegrippen van de (rechts)economie beschreven. Daarnaast wordt er gekeken naar de verzek…
Gerelateerde artikelen
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.