Dobbelstenen en wanorde, entropie uitgelegd
 Binnen het heelal wordt de wanorde steeds groter. Dit is een onomkeerbaar proces. Zoals de tijd, zoals het ouder worden. Deze natuurwet is onverbiddelijk. Het opheffen van (plaatselijke) wanorde, zoals het ontstaan van een organisme, kan alleen maar plaatsvinden als de wanorde eromheen nog sterker toeneemt. Dit is een consequentie van de tweede wet van de thermodynamica die zegt dat bij processen de hoeveelheid omgezette energie nooit volledig kan worden omgezet in arbeid. Er gaat altijd energie verloren in de vorm van warmte, het rendement van een proces is derhalve altijd kleiner dan 100%. Die verloren energie gaat zitten in een toegenomen wanorde. De wetenschap gebruikt hiervoor het begrip entropie. Bij een spontaan proces neemt de entropie toe. Het streven naar maximale entropie laat zich eenvoudig uitleggen aan de hand van het gedrag van dobbelstenen.
Binnen het heelal wordt de wanorde steeds groter. Dit is een onomkeerbaar proces. Zoals de tijd, zoals het ouder worden. Deze natuurwet is onverbiddelijk. Het opheffen van (plaatselijke) wanorde, zoals het ontstaan van een organisme, kan alleen maar plaatsvinden als de wanorde eromheen nog sterker toeneemt. Dit is een consequentie van de tweede wet van de thermodynamica die zegt dat bij processen de hoeveelheid omgezette energie nooit volledig kan worden omgezet in arbeid. Er gaat altijd energie verloren in de vorm van warmte, het rendement van een proces is derhalve altijd kleiner dan 100%. Die verloren energie gaat zitten in een toegenomen wanorde. De wetenschap gebruikt hiervoor het begrip entropie. Bij een spontaan proces neemt de entropie toe. Het streven naar maximale entropie laat zich eenvoudig uitleggen aan de hand van het gedrag van dobbelstenen.
Wanorde
Als je 100 munten netjes op een grote plaat legt met de kop naar boven en vervolgens flink schudt waardoor die munten omhoog vliegen en weer terug tuimelen, zie je het aantal munten met munt boven toenemen. Maar je kunt schudden wat je wil, het gaat je niet lukken om alle munten met de munt naar boven te krijgen. Je zult zien dat uiteindelijk ongeveer 50 munten kop boven hebben en ongeveer 50 munten munt boven. Waarom lukt dit eigenlijk niet? De situatie is vergelijkbaar met een worp met dobbelstenen. Als je 100 dobbelstenen in één keer op tafel gooit, zou je stomverbaasd zijn als de som van de dobbelstenen 100 of 600 zou zijn. Het is in principe mogelijk, maar het zal niet gebeuren. Hoe zit dat?Gooien met meer dobbelstenen
We werpen achtereenvolgens met één, twee en drie dobbelstenen en zetten de kans uit tegen de waarde van de worp: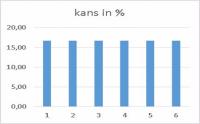
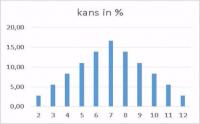
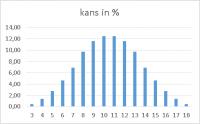
Toelichting
Als je met één dobbelsteen werpt, is er een kans van 1 op 6 om één van de zes waarden te gooien. In procenten 16,7 %. De gemiddelde waarde is 3,5. Als je met twee dobbelstenen werpt, wordt het anders. Er zijn in totaal 36 (6 x 6) mogelijkheden. Zo is er maar één mogelijkheid om 2 (of 12) te gooien, beide dobbelstenen moeten 1 (of 6) geven. De kans is (1/36)*100 = 2,8 %. De gemiddelde waarde zeven (2 x 3,5) kun je op verschillende manieren gooien: 1 - 6 en 6 - 1, 2 - 5 en 5 - 2, 3 - 4 en 4 - 3. Dit zijn zes mogelijkheden, kans 1/6, dus 16,7 %. Als je met drie dobbelstenen werpt, zijn er in totaal 216 (6 x 6 x 6) mogelijkheden. De kans op een drie (slechts één mogelijkheid) is 1/216, dus 0,5 %. De gemiddelde waarde is 3,5 x 3 = 10,5. De waarde 10 of 11 hebben een even grote kans. De tien kun je met de volgende waarden gooien: 1 - 3 - 6, 1 - 4 - 5, 2 - 2 - 6, 2 - 3 - 5, 2 - 4 - 4 en 3 - 3 - 4.Met drie verschillende waarden kan het op 6 manieren (voorbeeld: 136, 163, 316, 361, 613, 631), met twee verschillende waarden op 3 manieren. Totaal aantal mogelijkheden 6 + 6 + 3 + 6 + 3 + 3 = 27. Kans 27/216, dus 12,5 %.
De normaalverdeling
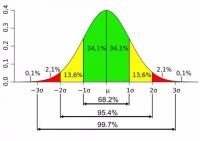 Bron: Dr Jody Muelaner, a Research Fellow at the University of Bath
Bron: Dr Jody Muelaner, a Research Fellow at the University of Bath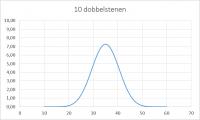
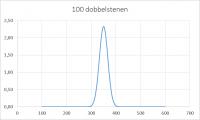
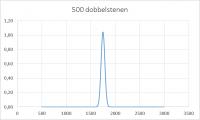
De kans op een extreme waarde wordt dus steeds kleiner, de kans op een worp rond de gemiddelde waarde wordt steeds groter. Waarom? Omdat deze waarde het grootste aantal realiseringsmogelijkheden heeft, met andere woorden de grootste entropie.
Experiment met 500 dobbelstenen
Een onderzoekje dat heel geschikt is voor in de klas. De docent vraagt de leerlingen voor de volgende les zoveel mogelijk dobbelstenen mee te nemen. "Haal ze uit alle spellen, van de zolder, bij opa en oma, de buren!" Met een klas van 30 leerlingen kom je dan al gauw op 500 dobbelstenen. Er wordt een superworp uitgevoerd en de docent voorspelt de uitkomst. Die docent heeft wat voorwerk verricht. Als hij een marge neemt van een 3% foute voorspelling is de kans dat de waarde na een worp 1750 ± 50 is zo'n 80%. "Ik voorspel dat gemiddeld 4 van de 5 worpen een waarde tussen de 1700 en 1800 oplevert". Succes verzekerd.Van dobbelstenen naar moleculen
In een gas is de gemiddelde onderlinge afstand tussen de moleculen ongeveer 10 maal de eigen afmeting. Als je een ruimte hebt van 1 m3 bevinden zich hierin onder normale omstandigheden 2,5.1025 moleculen (Verplaats de komma 25 plaatsen naar rechts: 25 met 24 nullen erachter). Dat zijn dan 10x10x10x2,5.1025 = 2,5.1028 "hokjes" waarin deze moleculen passen. De normaalverdeling is bij deze enorm grote getallen extreem smal, zo smal dat je kunt zeggen dat de toestand waarbij de moleculen gelijkmatig in de ruimte zijn verdeeld 100% waarschijnlijk is. Daarom verspreidt een gas zich in de ruimte. Daarom zullen verschillende gassen zich spontaan met elkaar vermengen.Niet-spontane processen
Bij het leggen van een puzzel neemt de entropie duidelijk af. De 'normale' toestand van een puzzel is in de doos met de losse stukjes door elkaar, of nog erger verspreid door het huis en misschien wel over de vuilnisbelt. Dat kan zomaar (spontaan) gebeuren. Een gelegde puzzel lijkt tegen de tweede hoofdwet in te gaan, maar dan wordt vergeten dat de puzzelaar heel wat inspanning heeft moeten verrichten, waarbij er van alles is gebeurd waardoor de entropie binnen hem en in zijn omgeving is toegenomen. Het nettoresultaat is altijd een toename van de entropie.Uiteindelijk stopt bij maximale entropie alles
Door de toename van de entropie neemt de hoeveelheid energie die kan worden omgezet in arbeid af. Uiteindelijk zal het universum vastlopen. Al het leven en alle beweging zullen ophouden omdat alle energie bij deze maximale wanorde is omgezet in onbruikbare energie waardoor er geen arbeid kan worden verricht en het leven niet langer mogelijk is. Dat is de natuurlijke gang van zaken: batterijen lopen leeg, machines gaan kapot, gebouwen verbrokkelen, wegen gaan op in wildernis, we sterven. Alles zal ophouden te functioneren tot in de eeuwigheid. Sommige theologen zeggen dat omdat het nu nog niet zover is, we die oneindigheid nog niet bereikt hebben. Zij concluderen daaruit dat er dan een begin moet zijn waarbij alles in gang is gezet. Maar dat is weer een heel ander onderwerp.© 2017 - 2025 3s4u, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Entropie, de orde of wanorde van energieAls we om ons heen kijken dan lijkt het universum waarin we leven één groot geheel te zijn van allerlei systemen die per…
Entropie, de orde of wanorde van energieAls we om ons heen kijken dan lijkt het universum waarin we leven één groot geheel te zijn van allerlei systemen die per…
 Gezelschapsspelletjes: Nieuwe dobbelspelenGezellig met zín allen spelletjes spelen. Gezamenlijk in een vertrouwd gezelschap, meer dan alleen tijdverdrijf. Lees hi…
Gezelschapsspelletjes: Nieuwe dobbelspelenGezellig met zín allen spelletjes spelen. Gezamenlijk in een vertrouwd gezelschap, meer dan alleen tijdverdrijf. Lees hi…
 Aardbevingen in Mexico-Stad versterkt door de bodemDe Mexicaanse vlag toont een afbeelding van een adelaar met een slang in zijn bek zittend op een cactus. Dit houdt verba…
Aardbevingen in Mexico-Stad versterkt door de bodemDe Mexicaanse vlag toont een afbeelding van een adelaar met een slang in zijn bek zittend op een cactus. Dit houdt verba…
 De zware herfststorm van 13 september 2017Na de voorjaarsstorm Doris van 23 februari 2017 en de zomerstorm van 6 juni in hetzelfde jaar beleefde Nederland op 13 s…
De zware herfststorm van 13 september 2017Na de voorjaarsstorm Doris van 23 februari 2017 en de zomerstorm van 6 juni in hetzelfde jaar beleefde Nederland op 13 s…
Gerelateerde artikelen
Zwaartekracht slechts entropisch verschijnselHoewel we er iedere seconde mee te maken hebben en de grootste wetenschappers zich er over hebben gebogen, weten we nog…
Percentielscores: uitleg en interpretatieSteeds vaker zijn percentielscores te zien bij de resultaten van toetsen en testen. Percentielen worden vaak onterecht v…
Bronnen en referenties
- Inleidingsfoto: Alexas Fotos, Pixabay (bewerkt)
- Dice Probability Calculator van Jasper Flick, http://anydice.com/
- Entropy and causality used as a proof for God's existence door Matt Slick, https://carm.org/entropy-and-causality-used-proof-gods-existence
- Afbeelding bron 1: Dr Jody Muelaner, a Research Fellow at the University of Bath (http://www.muelaner.com/wp-content/uploads/2013/07/Standard_deviation_diagram.png)
3s4u (17 artikelen)
Laatste update: 27-10-2017
Rubriek: Wetenschap
Subrubriek: Natuurverschijnselen
Bronnen en referenties: 4
Laatste update: 27-10-2017
Rubriek: Wetenschap
Subrubriek: Natuurverschijnselen
Bronnen en referenties: 4
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.