Binaire coderingen
 In de digitale wereld rekent men met enen en nullen; het zogenaamde binaire talstelsel. Dit talstelsel heeft het grondgetal twee. Hiermee verwant is het hexadecimale stelsel, met grondgetal 16. Er zijn verschillende coderingen mogelijk. In de digitale techniek wil men ook met negatieve getallen en cijfers achter de komma werken. De meest voorkomende codes zijn straight binary, de BCD code, de two's complement notatie, en de floating point notatie.
In de digitale wereld rekent men met enen en nullen; het zogenaamde binaire talstelsel. Dit talstelsel heeft het grondgetal twee. Hiermee verwant is het hexadecimale stelsel, met grondgetal 16. Er zijn verschillende coderingen mogelijk. In de digitale techniek wil men ook met negatieve getallen en cijfers achter de komma werken. De meest voorkomende codes zijn straight binary, de BCD code, de two's complement notatie, en de floating point notatie.Verschillende vormen van binaire codering
De meest gebruikelijke binaire representatie van een getal noemt men 'straight binary'. Deze code werkt precies zo als de decimale getalrepresentatie, met als enige verschil dat het grondgetal 2 wordt gebruikt in plaats van grondgetal 10.De straight binary code wordt echter lang niet altijd gebruikt door ontwerpers van hardware. Alle mogelijke berekeningen moeten door hardware uitgevoerd kunnen worden. Sommige coderingen zijn geschikter om bepaalde rekenkundige operatie's hardware-matig op te lossen dan andere. Zo vergemakkelijkt de two's complement-notatie het rekenen met getallen die ook negatief kunnen zijn. Zijn zeer precieze berekeningen vereist op komma-getallen, dan gebruikt men de floating point notatie. De BCD-code is een geschikte notatie om getallen op 7-segment displays zichtbaar te maken.
Daarnaast zijn er fout-herstellende coderingen in gebruik, wat de betrouwbaarheid van hardware vergroot. In bepaalde metingen of meet-opstellingen worden coderingen gebruikt die de betrouwbaarheid van de meting vergroten, zoals de Gray-code.
Getalrepresentatie's
De standaard methode om een getal te representeren is door het getal uit te drukken in machten van het grondgetal. Stel het grondgetal is g, dan:- getal = z (g)n + y (g)n-1 + … + d (g)3 + c (g)2 + b (g)1 + a (g)0
- de schrijfwijze van dit getal = 'z y x … e d c b a'
De cijfers (of digits) a, b, c, … z die gebruikt mogen worden zijn allen lager dan g. Zo betekent in ons gebruikelijke decimale stelsel (digits lager dan 10) het getal 457 het volgende:
- 457 = 400 + 50 + 7 = 4(10)2 + 5(10)1 + 7(10)0
Straight binary
In het binaire talstelsel gebruikt men het getal 2 als grondgetal, wat betekent dat we het getal g moeten schrijven als:
- getal = z (2)n + y (2)n-1 + … + d(2)3 + c(2)2 + b(2)1 + a(g)0
- we mogen alleen digits 0 en 1 gebruiken (allen lager dan 2)
- 457 = 256 + 128 + 64 + 8 + 1 = 1(2)8 + 1(2)7 + 1(2)6 + 0(2)5 + 0(2)4 +1(2)3 +0(2)2 + 0(2)1 + 1(2)0, dus binair genoteerd als: 1 1101 1001
Hexadecimaal
Hexadecimale codes worden gebruikt omdat ze makkelijker afleesbaar zijn dan binaire codes (bijvoorbeeld bij grote getallen). Het hexadecimale stelsel gebruikt 16 als grondgetal. De te gebruiken digits zijn 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, en F (allen lager dan 16). A heeft hier de decimale waarde van 10 en F de waarde 15:
- 277 = 1(16)2 + 1(16)1 + 5(16)0, dus hexadecimaal genoteerd als: 115
- 31 = 1(16)1 + F(16)0, dus hexadecimaal genoteerd als: 1F
| decimaal | binair | hexadecimaal |
|---|---|---|
| 0 | 0000 0000 | 00 |
| 1 | 0000 0001 | 01 |
| 7 | 0000 0111 | 07 |
| 8 | 0000 1000 | 08 |
| 15 | 0000 1111 | 0F |
| 16 | 0001 0000 | 10 |
| 31 | 0001 1111 | 1F |
| 32 | 0010 0000 | 20 |
| 63 | 0011 1111 | 3F |
| 64 | 0100 0000 | 40 |
BCD code
 -fig 1-
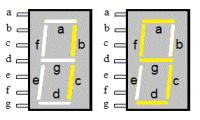
-fig 1-7-segment display, 2 digits
- 1 → 0001
- 5 → 0101
- 15 → 0001 0101
De BCD code is vooral handig, wanneer we getallen willen weergeven met een 7-segment display. Worden meer dan een digits gebruikt om een decimaal getal te presenteren aan een gebruiker, dan kan elk afzonderlijk display (digit) worden aangestuurd met een BCD-getal dat de decimale digit representeert.
In het bovenstaande voorbeeld (het decimale getal 15) zouden twee display's nodig zijn:
- display 1 wordt aangestuurd met 0001, wat de segmenten b en c doet oplichten.
- display 2 wordt aangestuurd met 0101, wat de segmenten a, f, g, c, en d doet oplichten.
| decimaal | straight binary | BCD |
|---|---|---|
| 1 | 0000 0001 | 0000 0001 |
| 13 | 0000 1101 | 0001 0011 |
| 25 | 0001 1001 | 0010 0101 |
Two's Complement
De two's complement notatie wordt gebruikt om negatieve getallen weer te geven. De twee meest gebruikte operatie's in hardware zijn optellen en vermenigvuldigen. Dit moet natuurlijk ook mogelijk te zijn voor negatieve getallen, daarom is een handigheidje ingevoerd:- een negatief getal geeft men weer door alle bits om te keren en er '1' bij op te tellen
Negatieve getallen hebben daardoor als hoogste bit altijd een '1'. Stel we hebben 4 bits ter beschikking, normaliter kunnen we daarmee de getallen 0, 1, …, 15 aangeven:
- 4 bits = 16 getallen = inclusief negatieve getallen -8, -7, -6, …, -1, 0, 1, 2, …, 7
- in de two's complement notatie geeft men het getal -1 weer als (omkeren(0001) + 1) = (1110 + 1) = 1111
We kunnen nu de som -1 + 1 = 0 uitvoeren:
1111
0001 +
------
0000
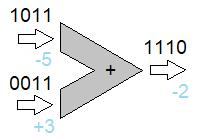 -fig 2- Digitale optelling
-fig 2- Digitale optellingOok andere sommatie's gaan goed; -5 + 3 = -2:
1011
0011 +
------
1110
| decimaal | 7 | .... | 1 | 0 | -1 | -2 | .... | -8 |
|---|---|---|---|---|---|---|---|---|
| two's complement | 0111 | .... | 0001 | 0000 | 1111 | 1110 | .... | 1000 |
Floating point
De floating point notatie wordt gebruikt om niet-gehele getallen aan te geven. Men noemt het ook wel zwevende komma. De algemene notatie is als volgt:- N = m r exp
met
- N = floating point getal
- m = mantisse
- r = radix (grondgetal)
- exp = exponent
Een floating point getal heeft een eindige precisie; het aantal cijfers achter de komma wordt beperkt door het aantal bits dat men tot de beschikking heeft. Er zijn verschillende afspraken mogelijk over het formaat van een floating point getal.
Meestal neemt men voor de radix het getal 2 en geldt de afspraak dat er maar 1 digit voor de komma staat. In de binaire stelsel is dit dus altijd een '0' of een '1', men kan ervoor kiezen deze digit niet weer te geven. Ook kan men ervoor kiezen de exponent weer te geven met een offset, bijvoorbeeld exponent = (werkelijke exponent + offset). Hiermee vergroot men het bereik (als de exponent alleen nullen bevat, is de werkelijke exponent gelijk aan (-offset)). Vaak gebruikt men nog een extra bit om het teken van het getal aan te geven, het zogenaamde sign-bit.
Zodoende kan een 32-bits floating getal kan er als volgt uit zien:
- N = (-1) sign-bit * 2 (exp-127) * 1.mantisse
- N(32:0) = [sign-bit(32), exponent(31:24), mantisse(23:0)]