De wet van Ohm en ohmse weerstand
 Georg Ohm (1787-1854) was een Duitse wis- en natuurkundige. Hij legde het verband tussen elektrische spanning en stroom vast in de wet van Ohm. Dit was een resultaat van zijn onderzoek naar warmte-ontwikkeling bij elektrische stroom. Het begrip elektrische weerstand (=spanning/stroom) werd ingevoerd. De eenheid Ω voor elektrische weerstand is naar Ohm vernoemd. Wanneer we de elektrische weerstand van een systeem weten, kan de bijbehorende stroom door een component of circuit worden uitgerekend.
Georg Ohm (1787-1854) was een Duitse wis- en natuurkundige. Hij legde het verband tussen elektrische spanning en stroom vast in de wet van Ohm. Dit was een resultaat van zijn onderzoek naar warmte-ontwikkeling bij elektrische stroom. Het begrip elektrische weerstand (=spanning/stroom) werd ingevoerd. De eenheid Ω voor elektrische weerstand is naar Ohm vernoemd. Wanneer we de elektrische weerstand van een systeem weten, kan de bijbehorende stroom door een component of circuit worden uitgerekend.De wet van Ohm
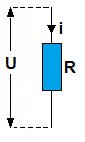 -fig 1-
-fig 1-U = I • R
- U = I • R [V]
Hierin staan de grootheden:
- U voor elektrische spanning; eenheid Volt [V]
- I voor stroomsterkte; eenheid Ampère [A]
- R voor de weerstand; eenheid Ohm [Ω]
De wet van Ohm beschrijft het verband tussen elektrische spanning en stroomsterkte. Tussen twee punten A en B in een geleider is de spanning gelijk aan het product van stroomsterkte (van A naar B) en de weerstand. Voorwaarde is dat de weerstand R constant is; de temperatuurafhankelijk van R is geen onderdeel van de wet van Ohm.
Weerstand en geleiding
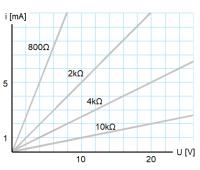 -fig 2-
-fig 2-- het quotiënt R = U / I [Ω] wordt ohmse weerstand genoemd
- 1 / R = G = de geleiding [S]
- geleiders voldoen aan de wet van Ohm
De geleiding G (eenheid [S], Siemens) is het omgekeerde van de weerstand. Materialen hebben verschillende ohmse weerstanden, voor een isolator geldt dat de ohmse weerstand zeer hoog (ideaal oneindig) is.
In halfgeleiders - zoals diodes en transistoren - zijn de (spanning-stroom)karakteristieken niet-lineair. Voor supergeleiders geldt dat de weerstand gelijk aan nul is.
Weerstand in de praktijk
Bij gegeven spanning zal de ohmse weerstand in een geleider de grootte van de stroomsterkte bepalen. Dit betekent dat een weerstand te gebruiken is als stroombegrenzer. Door meerdere weerstanden te gebruiken (een zogenaamde spanningsdeler) kan de spanning op een zeker punt worden vastgelegd.Weerstand als component
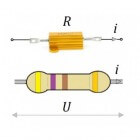
In de elektronica worden weerstanden gebruikt als component, en zijn beschikbaar in verschillende soorten en maten. De juiste weerstandswaarde kan gekozen worden met een zekere tolerantie (procentuele afwijking van de opgegeven waarde). De weerstandswaarde is beschikbaar in een voorgedefinieerde reeks, de zgn. E-reeks. Daarnaast zijn er weerstanden beschikbaar die aangepast zijn voor hogere vermogens.
De ohmse weerstand wordt meestal weergegeven door een kleurcode, aangebracht in een aantal ringen rond de weerstand. De kleurcode geeft de weerstandswaarde en de tolerantie (procentuele afwijking) van de weerstand aan, voor de ringen geldt het volgende:
 -fig 3-
-fig 3-- de 1e ring zit het dichtst bij het uiteinde
- de laatste ring kan zilver of goud zijn, de laatste ring zit op een wat grotere afstand van de rest
- de kleur van ring 1 en 2 staat voor een cijfer
- de kleur van volgende ring staat voor de exponent van 10 ('10 tot de macht cijfer')
- de kleur van de laatste ring staat voor de tolerantie
- de weerstandswaarde R = (kleur1, kleur2,...) * 10exponent ± tolerantie [Ω]
Weerstand in de installatietechniek
Alle elektrische apparaten die u in uw huis gebruikt hebben ook een elektrische weerstand of impedantie. Zo zal een lamp van 60 Watt ongeveer de volgende weerstand hebben (impedanties niet meegerekend):
- Vermogen = spanning * stroom = spanning * (spanning / weerstand) = 60 Watt.
- U2/R = 60 Watt
- R = U2 (Volt)/60 (Watt) = 2302/60 = 882 Ohm
(aangenomen dat de temperatuur constant is, en dus geen invloed heeft op de weerstandswaarde).
Ook de bedrading van het lichtnet in uw huis heeft een zekere weerstand. De installatie in uw huis verloopt vanaf de meterkast met zekeringen via installatiedraad en verdeeldozen naar alle wandcontactdozen ('stopcontact') en apparatuur. Dit installatiedraad is gemaakt van koper met een zekere doorsnede en daaromheen een kunststof isolator. De weerstand van zo'n draad kan men eenvoudig berekenen met behulp van de volgende formule:
- R = (l / A) * ρ
l = lengte draad, A = diameter draad [mm²], ρ = soortelijke weerstand van koper = 17,5 [mΩ/m]), een stuk installatiedraad met 1,5 mm² doorsnee en 10 meter lengte zal een weerstand hebben van: R = (10/1,5) * 17 mΩ = 116,7 mΩ
Deze waarde is erg laag. We willen graag dat de geleiders in ons lichtnet een zo laag mogelijke weerstand hebben. Over elke component met weerstand waardoor een stroom loopt zal ook een spanning (I *R) staan. De 230 Volt die u thuis krijgt aangeboden moet ten volle worden benut voor de apparatuur die erop aangesloten is. We willen niet dat een gedeelte van die 230 Volt verloren gaat.
Wisselstroomweerstand of impedantie
Voor gelijkspanningen (en gelijkstromen) geldt dat er geen faseverschil zal bestaan tussen de spanning en stroom. Een wisselspanning aangesloten op een belasting levert een wisselstroom op.Deze wisselstroom wordt niet alleen door ohmse weerstand bepaald, maar ook door inductieve en capacitieve weerstand. Inductief en capacitief gedrag van wisselstroomweerstand (of impedantie) zorgt voor een faseverschil dat opgewekt worden tussen de spanning en stroom (figuur 4).
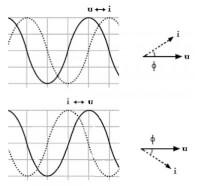 -fig 4-
-fig 4-stroom loopt voor of achter tov de spanning
- faseverschil = het stroomsignaal gaat voor- of achterlopen ten opzichte van het spanningssignaal
- voorlopen (is capacitief): het stroomsignaal verschuift naar voren met een fasehoek φ
- achterlopen (inductief), faseverschuiving φ naar achteren
We kunnen dit duidelijker zichtbaar maken door te rekenen met vectoren (complexe getallen). De vector (pijl) draait in het diagram rond met frequentie f, dit stelt een periodiek signaal (bv een sinus) voor. Een faseverschil tussen spanning en stroom ziet er in het diagram uit als twee vectoren die beide ronddraaien met frequentie f, en een onderlinge hoek φ.
Complexe schrijfwijze
Een impedantie kan ook weergegeven worden als vector, met een ohmse component R en een inductieve/capacitieve component X.
 -fig 5-
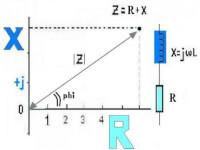
-fig 5-- De complexe schrijfwijze voor een impedantie is Z = R ± j*X.
- Zie figuur 5, de totale impedantie van een spoel met serieweerstand is Z = R + jωL
- de absolute waarde (grootte) van de vector: |Z| = √ (R² + X²)
- de fasehoek: phi = arctan (X / R)
Voor de grootte van de stroom geldt i(t) = U(t) / |Z|.