Lineaire regressie
Machine learning is het wetenschappelijke gebied dat algoritmen bestudeert die kunnen leren van data. Het leren van data heeft over het algemeen twee doelen: het voorspellen van het volgende stukje informatie of het classificeren van een stuk informatie. Het voorspellen van informatie is moeilijk en wordt in de praktijk niet veel toegepast. Echter, het voorspellen van informatie is zeer handig om bijvoorbeeld het weer te voorspellen.Het voorspellen van informatie
Aan de hand van ontvangen informatie kan een patroon worden ontdekt door een algoritme. Aan de hand van dit patroon kan het volgende stukje informatie worden voorspeld. Een simpel algoritme om dit patroon te vinden, is lineaire regressie. Het idee van lineaire regressie is om een wiskundig model te vinden. Dit wiskundige model wordt getest op de geobserveerde data. Het doel is om het verschil tussen het voorspelde datapunt en geobserveerde datapunt te minimaliseren. Het doel is om het verschil tussen het geobserveerde datapunt en voorspelde datapunt weg te werken, waardoor het model elk datapunt precies voorspelt, zoals geobserveerd. Aan dit model worden straffen toegekend. Dit zorgt ervoor dat het algoritme niet precies elk datapunt voorspelt, maar ook ongeziene data kan voorspellen.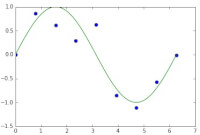
Figuur 1
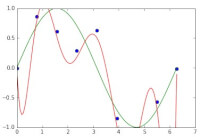Figuur 2
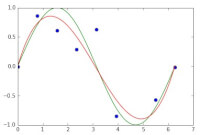Figuur 3Neem een sinusoïde. Dit is de echte functie. Echter, wanneer dit signaal wordt gezien in de praktijk is er altijd sprake van ruis. Hierdoor ligt niet elk datapunt precies op de sinus, maar er omheen. In figuur 1 zijn de blauwe datapunten de geobserveerde data. De groene lijn is de daadwerkelijke functie die we willen voorspellen.
Zoals eerder genoemd, is het doel nu om een functie te bedenken die elk datapunt correct voorspelt. Echter, later zorgen we er juist voor dat het algoritme fouten gaat maken. In figuur 2 wordt de data precies voorspeld, weergegeven door de rode lijn.
Hoewel het rode lijntje nu specifiek weergeeft elk datapunt voorspelt, komt het geleerde model niet overeen met de sinus. Dit betekent dat de gewenste functie dus niet wordt voorspeld. Door strafpunten in te voeren, zal het geleerde model niet elk datapunt precies voorspellen, maar het onderliggende model. Dit wordt weergegeven in figuur 3.
Zoals kan worden gezien, wordt het onderliggende model zo goed mogelijk benaderd. Het zou ideaal zijn om deze precies te benaderen, maar in de werkelijkheid is dit vaak niet mogelijk.
