Fractalen: definitie, theorie en voorbeelden
 De gelijkvormigheid van figuren hebben sinds het begin der tijden al een soort aantrekkingskracht gehad op de mens. Gelijkvormigheid valt terug te vinden in fractalen. Fractalen zijn heel speciale meetkundige figuren. Wat deze fractalen juist inhouden, is niet echt bekend bij de meeste mensen. Er valt echter zoveel meer te vertellen over deze wiskundige figuren dan enkel de wiskundige bewijzen. Ze bestaan namelijk niet enkel en alleen in de theoretische wiskunde, maar zijn ook overal te vinden in de natuur.
De gelijkvormigheid van figuren hebben sinds het begin der tijden al een soort aantrekkingskracht gehad op de mens. Gelijkvormigheid valt terug te vinden in fractalen. Fractalen zijn heel speciale meetkundige figuren. Wat deze fractalen juist inhouden, is niet echt bekend bij de meeste mensen. Er valt echter zoveel meer te vertellen over deze wiskundige figuren dan enkel de wiskundige bewijzen. Ze bestaan namelijk niet enkel en alleen in de theoretische wiskunde, maar zijn ook overal te vinden in de natuur.
Definitie fractal
Een fractal is een meetkundige figuur met als karakteristieke eigenschap dat onderdelen (details) van de figuur gelijkvormig zijn met de figuur zelf, maar op een kleinere schaal.Algemene theorie over fractalen
Gelijkvormigheid
Een fractal is een meetkundige figuur, waarvan een detail gelijkvormig met het geheel is. Zo treedt voortdurend een herhaling van patronen op bij het ‘inzoomen’, die door sommigen als zeer mooi wordt ervaren. Bij de ideale fractal komt de gelijkvormigheid steeds weer terug, elke keer als de schaalgrootte wordt verkleind, zeg maar: als wordt ingezoomd. Wanneer het aantal stapjes waarbij dit lukt, beperkt is, spreekt men van een pre-fractal.Herkomst naam 'fractal'
De naam ‘fractal’ is ontleend aan de wiskundige eigenschap dat de figuur een zogenaamde ‘gebroken dimensie’ heeft. Die dimensie is dan een zuiver wiskundig begrip (het dimensiebegrip van Hausdorff), en geeft het verband weer tussen de grootte van het zich herhalende gelijkvormige ‘puzzelstukje’ en het aantal puzzelstukjes dat nodig is om de totale fractal weer te maken.Terwijl een fractal een ingewikkelde structuur lijkt te hebben, is een enkele wiskundige vergelijking vaak al voldoende om die structuur helemaal te beschrijven.
Mandelbrot-verzameling
De Mandelbrot-verzameling levert op verschillende schalen een variëteit aan figuren, uitgaande van de vergelijking z = z² + c (met c als constante). Fractals kunnen een rol spelen in de zo kort mogelijke codering van beelden. Vanaf 1982 spande de wiskundige Benoit B. Mandelbrot zich in om de opmerkelijke eigenschappen van fractals in brede kring bekend te maken. In de jaren negentig hebben kunstenaars en amateur-wiskundigen met computers talrijke fractals gegenereerd. Maar juist vanwege de eenvoudige wiskunde achter complexe structuren, zijn fractals ideaal ter beschrijving van ingewikkelde patronen.In de natuur komen veel structuren voor die lijken op die van fractals. Ook kunnen fractals belangrijk zijn in het ophelderen van de manieren waarop de hersenen dingen herkennen. De hersenen werken hierbij met name op grond van gelijkenissen, wat in de wiskundige structuur van fractals lijkt te zijn ingebouwd.
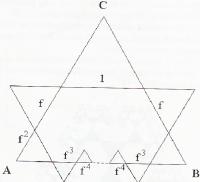
Verband fractal-Gulden Snede (φ)
Bewijs
Uit deze afbeelding blijkt dat:- AC = 1+ f + f ²
- AB = 2 . (f ² + f ³ + f 4 + …)
- 1 + f + f ² = 2 . (f ² + f ³ + f 4 + …) (AC = AB)
- f ² + f ³ + f 4 + … = f ²/(1 - f) en f ³ + 2f ² - 1 = 0 (formule meetkundige reeks)
- Daar f positief moet zijn, is de conclusie dat f = 1/φ
Verband
Bij sommige fractals is de gelijkvormigheidsfactor gelijk aan 1/φ Driehoek van Sierpinski / Bron: Momos, Pixabay
Driehoek van Sierpinski / Bron: Momos, PixabayVoorbeelden fractalen
Driehoek van Sierpinski
TheorieHet eerste voorbeeld van een fractal is de driehoek van Sierpinski. Deze fractal werd ontdekt door de Pool Wacław Sierpinski. Hij ontdekte namelijk een oneindige kromme die als voorloper wordt gezien van de fractal. De driehoek van Sierpinski ontstaat door het herhalen van een bepaalde werkmethode (zie opbouw) tot in het oneindige. Door het herhalen van deze werkmethode, wordt er een soort piramide gecreëerd. Een opmerkelijk feit aan deze fractal is dat zijn oppervlakte gelijk is aan 0 m².
Opbouw
- Teken een gelijkzijdige driehoek.
- Deel de driehoek op in vier gelijkzijdige driehoeken en laat de middelste weg.
- Herhaal dit proces.
 Tapijt van Sierpinski / Bron: TymonOziemblewski, Pixabay
Tapijt van Sierpinski / Bron: TymonOziemblewski, PixabayTheorie
De Poolse wiskundige Wacław Sierpiński heeft buiten de driehoek van Sierpinski nog een andere fractal beschreven: het tapijt van Sierpinski. Net zoals bij de driehoek van Sierpinski is de oppervlakte van het tapijt van Sierpiński gelijk aan 0 m². Als men het tapijt van Sierpinski in drie dimensies opbouwt, bekomt men een nieuwe fractal. Men noemt deze driedimensionale fractal ook wel de Spons van Menger.
Opbouw
- Teken een vierkant
- Deel het vierkant op in negen gelijke vierkanten en laat het middelste vierkant weg.
- Herhaal dit proces voor elk vierkant.
 Boom van Pythagoras / Bron: Dibargatin, Openclipart
Boom van Pythagoras / Bron: Dibargatin, OpenclipartTheorie
Een zeer bekende fractal is de boom van Pythagoras. Deze fractal werd beschreven door de Nederlander Albert Bosman in het jaar 1942. Deze Nederlandse wiskundige vernoemde de ontdekte fractal naar de Grieks wiskundige Pythagoras door de aanwezigheid van zijn typische driehoeksverhoudingen met de bekende hoek van 90°. Zoals reeds vermeld is de fractal geconstrueerd door oneindig veel vierkanten en men verwijst hier soms naar als de bloemkool-vormige fractal.
Opbouw
- Teken een vierkant
- Op het vierkant construeren we een rechthoekige driehoek met de schuine zijde (de bovenste zijde van het vierkant). Teken langs de rechthoekszijden nieuwe vierkanten. Dankzij de stelling van Pythagoras weet men dat de opgetelde oppervlaktes van de twee nieuwe, kleine vierkanten gelijk is aan de oppervlakte van het eerste grote vierkant.
- Herhaal dit proces voor elk vierkant.
 Sneeuwvlok van Koch / Bron: Kindlychung, Openclipart
Sneeuwvlok van Koch / Bron: Kindlychung, OpenclipartTheorie
De Zweed Helge von Koch ontdekte in 1904 een kromme die later de kromme van Koch zou gedoopt worden. De kromme is op zichzelf al een fractal, maar ook de basis van een iets bekendere fractal, namelijk: de sneeuwvlok van Koch.
Opbouw
- Teken een gelijkzijdige driehoek
- Deel de zijden op in drie gelijke stukken en vervang het middelste door een gelijkzijdige driehoek en laat de basis weg.
- Herhaal dit proces voor elke zijde.
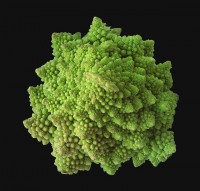 Romanesco / Bron: Delannya, Pixabay
Romanesco / Bron: Delannya, Pixabay Romanesco is een mooi voorbeeld van een fractal in de natuur / Bron: Hans, Pixabay
Romanesco is een mooi voorbeeld van een fractal in de natuur / Bron: Hans, Pixabay Ook het blad van een varen is een mooi voorbeeld van een fractal in de natuur / Bron: Pattyjansen, Pixabay
Ook het blad van een varen is een mooi voorbeeld van een fractal in de natuur / Bron: Pattyjansen, Pixabay© 2016 - 2025 Blueyann, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Een bijzondere fractal: de driehoek van SierpinskiDe Poolse wiskundige Waclaw Sierpinski verrichte baanbrekend werk in de wiskunde, met name in de verzamelingenleer. Voor…
Een bijzondere fractal: de driehoek van SierpinskiDe Poolse wiskundige Waclaw Sierpinski verrichte baanbrekend werk in de wiskunde, met name in de verzamelingenleer. Voor…
 Stelling van PythagorasMet de stelling van Pythagoras kun je de lengtes van de zijden van een rechthoekige driehoek berekenen. De stelling is r…
Stelling van PythagorasMet de stelling van Pythagoras kun je de lengtes van de zijden van een rechthoekige driehoek berekenen. De stelling is r…
 Pythagoras, de wiskundige en filosoofPythagoras was een Griekse wiskundige en filosoof die zeer veel verschillende experimenten heeft uitgevoerd. Het grootst…
Pythagoras, de wiskundige en filosoofPythagoras was een Griekse wiskundige en filosoof die zeer veel verschillende experimenten heeft uitgevoerd. Het grootst…
 Filosoof uitgelicht; Pythagoras van SamosDe stelling van Pythagoras, deze stelling is bekend bij velen. Maar wie was nu Pythagoras. Een educatieve toelichting op…
Filosoof uitgelicht; Pythagoras van SamosDe stelling van Pythagoras, deze stelling is bekend bij velen. Maar wie was nu Pythagoras. Een educatieve toelichting op…
 De MANOVA of multivariantie-analyseDe multivariate analysis of variance, meestal afgekort tot MANOVA, is een statistische analysemethode. Net zoals bij de…
De MANOVA of multivariantie-analyseDe multivariate analysis of variance, meestal afgekort tot MANOVA, is een statistische analysemethode. Net zoals bij de…
Gerelateerde artikelen
Wiskundige bewijstechniekenIn de wiskunde wordt elke bewering, propositie of stelling bewezen voor men aanvaardt dat hij waar is. Het is zowat het…
Bronnen en referenties
- Inleidingsfoto: PIRO4D, Pixabay
- KLEIJNE W. en KONINGS T., De Gulden Snede. Utrecht, 2000
- HET LAATSTE NIEUWS, Van Fas tot Ger In: Spectrum. Encyclopedie in 25 delen. 2005, dl. 9
- SCIENTIAS, https://www.scientias.nl/wat-zijn-fractals-en-zijn-ze-nuttig/, geraadpleegd op 17-09-2016
- http://fractalfoundation.org/resources/what-are-fractals/, geraadpleegd op 17-09-2016
- http://mathworld.wolfram.com/Fractal.html, geraadpleegd op 17-09-2016
- http://www.fractalen.net/html/algemeen.html, geraadpleegd op 17-09-2016
- Afbeelding bron 1: Momos, Pixabay
- Afbeelding bron 2: TymonOziemblewski, Pixabay
- Afbeelding bron 3: Dibargatin, Openclipart
- Afbeelding bron 4: Kindlychung, Openclipart
- Afbeelding bron 5: Delannya, Pixabay
- Afbeelding bron 6: Hans, Pixabay
- Afbeelding bron 7: Pattyjansen, Pixabay
Blueyann (26 artikelen)
Gepubliceerd: 19-09-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 14
Gepubliceerd: 19-09-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 14
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.