Goniometrische functies differentiëren en integreren
 Goniometrische functies behandelen is een lastige zaak. Er moet met veel rekening worden gehouden, zoals of de functie een cosinus of een sinus bevat, of er een minteken aanwezig is en wat er tussen de haken staat die de goniometrische functie definieert. In de praktijk blijkt dit vaak nog een lastige opgave die ervoor zorgt dat vele opgaven op de klippen lopen. Met inachtneming van de bovenstaande aspecten, en enkele rekenregels, zijn veel functies simpel op te lossen.
Goniometrische functies behandelen is een lastige zaak. Er moet met veel rekening worden gehouden, zoals of de functie een cosinus of een sinus bevat, of er een minteken aanwezig is en wat er tussen de haken staat die de goniometrische functie definieert. In de praktijk blijkt dit vaak nog een lastige opgave die ervoor zorgt dat vele opgaven op de klippen lopen. Met inachtneming van de bovenstaande aspecten, en enkele rekenregels, zijn veel functies simpel op te lossen.
Goniometrische functies
Goniometrische functies zijn functies die een golfbeweging beschrijven. Deze functies bestaan uit een evenwichtsstand a, een amplitude b, een periode c en een x-coordinaat van het beginpunt d. De grootte van de periode, dus de lengte waarin één golf wordt voldaan, is gelijk aan 2π/c. De algemene formules voor zowel de sinus als de cosinus zijn hieronder weergegeven:Sinusfunctie: a + b sin(cx + d)
Cosinusfunctie: a + b cos(cx + d)
Cosinusfunctie: a + b cos(cx + d)
Het differentiëren en het integreren van deze functies is een relatief simpele taak, alhoewel het vaak als een grote moeilijkheid wordt ervaren. Toch kan, met behulp van simpele rekenregels en theorie, met veel gemak een dergelijke opgave worden opgelost.
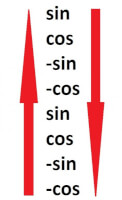 Figuur 1: repetitief patroon bij integreren en differentiëren
Figuur 1: repetitief patroon bij integreren en differentiërenRekenregels bij sin/cos
Bij het differentiëren en integreren van een goniometrische functie verandert de hele formule. Een opmerkelijk feit is dat een sinus of cosinus daarentegen nooit weg kan worden gedifferentieerd of geïntegreerd. In figuur 1 wordt dit aspect van een goniometrische functie duidelijker: uiteindelijk blijft een sinus of cosinus voortbestaan in de functie, ongeacht van de hoeveelheid keren deze wordt gedifferentieerd of geïntegreerd. Daarnaast worden in figuur 1 grote, rode pijlen weergegeven. De rode pijl geeft de integrerende richting aan. Bij een simpele functie, bijvoorbeeld f(x) = cos(x), houdt dit in dat de primitieve van de functie f(x), ook wel aangegeven als F(x), gelijk is aan F(x)=sin(x). Omdat deze functie zeer simpel is verandert alleen de cosinus naar een sinus. Een functie differentiëren komt op hetzelfde neer. Een voorbeeldfunctie in dit geval is g(x) = x - cos(x). In dit geval moet de somregel worden gebruikt. Dit houdt in dat de afgeleide van functie g(x), ook wel aangegeven als g'(x), gelijk is aan g'(x) = [x]' - [cos(x)]', oftewel g'(x) = 1 + sin(x). Of het negatieve teken wordt meegenomen bij het differentiëren of integreren is niet van belang. Het is mogelijk om het negatieve teken mee te nemen, maar het beïnvloedt de nieuwe formule niet. Hierdoor is het makkelijker om deze buiten beschouwing te laten.Omzettingsformules
Sommige opgaven vertonen een zeer complexe formule die op zijn beurt ook moeilijk kan zijn om te differentiëren of integreren. Uiteraard is het mogelijk om de formule, zoals die staat aangegeven, te behandelen, maar er bestaan ook omzettingsformules, ook wel verdubbelingsformules genoemd, om deze functies te versimpelen zodat er veel tijd en moeite wordt bespaard. In onderstaand voorbeeld wordt de werking van een verdubbelingsformule uitgelegd.Bereken de afgeleide van f(x) = cos(x) - 2 cos(x)sin²(x)
- Zet eerst de cosinus buiten de haken: f(x) = cos(x) (1 - 2 sin²(x))
- Een verdubbelingsformule die hier gebruikt kan worden is: cos(2A) = 1 - 2 sin²(A)
- Dit geeft: f(x) = cos(x) * cos(2x)
- De productregel gebruiken geeft: f'(x) = [cos(x)]' * cos(2x) + cos(x) * [cos(2x)]'
- Dit geeft als uiteindelijke afgeleide: f'(x) = -sin(x)cos(2x) - 2 cos(x)sin(2x)
 Figuur 2: vraag 9 bij het CE wiskunde B, eerste tijdvak, 2017
Figuur 2: vraag 9 bij het CE wiskunde B, eerste tijdvak, 2017Op het domein [0, π] is de functie f gegeven door f(x) = 3 sin(x) - 2 sin²(x). De grafiek snijdt de x-as in (0, 0) en (π, 0). Het gebied V wordt ingesloten door f(x) en de x-as. Bereken exact de oppervlakte van V. Zie figuur 2.
Deze vraag werd gesteld in het eerste tijdvak van het centraal examen van wiskunde B in 2017. De moeilijkheid van deze vraag zit in het kwadratische gedeelte. Het is mogelijk om de functie f(x), zoals hij in de vraag staat vermeld, te integreren naar zijn primitieve, alleen maakt de kwadratische sinus het proces erg omslachtig en moeilijk. Een andere optie is om de sin(x) gelijk te stellen aan p en zo verder werken, maar deze manier maakt het integreren niet heel erg makkelijker. De makkelijkste optie is om de verdubbelingsformules te gebruiken en aan te passen naar de situatie zodat de functie geen kwadratische term meer bevat. Onderstaand voorbeeld maakt gebruikt van de verdubbelingsformules om de kwadratische sinus weg te werken, waardoor met enkele opvolgende stappen de opgave doeltreffend en snel wordt opgelost.
De oppervlakte moet worden gevonden, dus de integraal van f(x) moet lopen van 0 tot π. Als eerst moet de huidige functie f(x) versimpeld worden: f(x) = 3 sin(x) - 2 sin²(x).
- De eerste stap is de kwadratische sinus omzetten met de verdubbelingsformules. cos(2A) = 1 - 2 sin²(A) kan worden omgezet naar: - 2 sin²(A) = cos(2A) - 1
- Invullen geeft: f(x) = 3 sin(x) + cos(2x) - 1
- Deze functie is makkelijk te integreren, wat de volgende primitieve geeft: F(x) = -3 cos(x) + ½ sin(2x) - x
- De integraal moet lopen van 0 tot π, dus de oppervlakte V is gelijk aan: F(π) - F(0)
- Dit geeft: V = (-3 cos(π) + ½ sin(π) - π) - (-3 cos(0) + ½ sin(0) - 0)
- Doorberekenen geeft: V = (3 + 0 - π) - (-3 + 0 - 0)
- De oppervlakte: V = 3 - π + 3 = 6 - π
Voorbeeld 2: Kettingregel in goniometrie
De kettingregel in goniometrische formules berust op hetzelfde principe als de andere situaties waarin de kettingregel wordt gebruikt. Een voorbeeld is de functie d(x) = 3 cos(2x² + 3x - ½π). In deze functie moet hetgeen wat tussen de haken staat als aparte functie worden beschouwd. In onderstaand veld wordt dit voorbeeld uitgelegd.Gegeven is de functie: d(x) = 3 cos(2x² + 3x - ½π)
- Deze functie moet eerst worden omgezet naar: d(u) = 3 cos(u) met u(x) = 2x² + 3x - ½π
- Als eerst moet de afgeleide worden gevonden van u(x), dit is: u'(x) = 4x + 3
- Daarna moet de afgeleide worden gevonden van d(u), dit is: d'(u) = -3 sin(u)
- Vervolgens is de afgeleide van d(x), oftewel d'(x), op te stellen volgens de kettingregel: d'(x) = d'(u) * u'(x)
- Dit is: d'(x) = -3 sin(u) * (4x + 3)
- U substitueren voor de functie zelf geeft:
- d'(x) = -3 sin(2x² + 3x - ½π) * (4x + 3), oftewel
- d'(x) = (-12x - 9) sin (2x² + 3x - ½π)
© 2017 - 2025 Dysprosium, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Goniometrie - theorie en voorbeeldenIn de technische wiskunde wordt veel gewerkt met vaardigheden zoals algebra en meetkunde. Zo moeten functies gelijk zijn…
Goniometrie - theorie en voorbeeldenIn de technische wiskunde wordt veel gewerkt met vaardigheden zoals algebra en meetkunde. Zo moeten functies gelijk zijn…
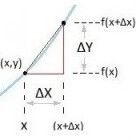 Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
 Differentiëren met de TI grafische rekenmachinesDe grafische rekenmachines van Texas Instruments worden anno 2014 veel gebruikt in het voortgezet en hoger onderwijs, bi…
Differentiëren met de TI grafische rekenmachinesDe grafische rekenmachines van Texas Instruments worden anno 2014 veel gebruikt in het voortgezet en hoger onderwijs, bi…
 Profielkeuze; Natuur & TechniekAl op jonge leeftijd moeten leerlingen een belangrijke keuze maken voor de toekomst. In de derde klas van zowel de HAVO…
Profielkeuze; Natuur & TechniekAl op jonge leeftijd moeten leerlingen een belangrijke keuze maken voor de toekomst. In de derde klas van zowel de HAVO…
 Excel: één werkblad voor talloze grafiekenIn Microsoft Excel zijn op eenvoudige wijze grafieken te maken. Door in het werkblad aan cellen de waarden van de coëffi…
Excel: één werkblad voor talloze grafiekenIn Microsoft Excel zijn op eenvoudige wijze grafieken te maken. Door in het werkblad aan cellen de waarden van de coëffi…
 Vermenigvuldigingen van lange getallen in je hoofd berekenenHoe doen van berekeningen hoort in ons dagelijkse bestaan en dus wordt er op school ook veel aandacht aan gegeven. Ieder…
Vermenigvuldigingen van lange getallen in je hoofd berekenenHoe doen van berekeningen hoort in ons dagelijkse bestaan en dus wordt er op school ook veel aandacht aan gegeven. Ieder…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Geralt, Pixabay
- https://www.examenblad.nl/examen/wiskunde-b-vwo/2017
- http://www.wisfaq.nl/pagina.asp?nummer=1457
- http://www.hhofstede.nl/modules/verdubbelingsformules.htm
- http://math4allview.appspot.com/view?comp=vb-d1&subcomp=vb-d12&variant=m4a_view&repo=m4a2015&item=theory
Dysprosium (40 artikelen)
Gepubliceerd: 07-09-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Gepubliceerd: 07-09-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.