Wiskunde de afgeleide en differentiëren
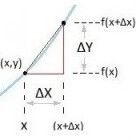 De afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y). Het geeft de waarde van de richtingcoëfficiënt van de raaklijn in (x,y) aan. Het bepalen van de afgeleide is een essentieel onderdeel van de wiskunde. De afgeleide van een functie bepalen wordt toegepast in allerlei vakgebieden. Uitleg en enkele voorbeelden van afgeleide's van bekende veelgebruikte functie's.
De afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y). Het geeft de waarde van de richtingcoëfficiënt van de raaklijn in (x,y) aan. Het bepalen van de afgeleide is een essentieel onderdeel van de wiskunde. De afgeleide van een functie bepalen wordt toegepast in allerlei vakgebieden. Uitleg en enkele voorbeelden van afgeleide's van bekende veelgebruikte functie's.
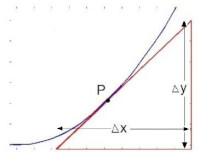 -fig 1- / Bron: Tronic
-fig 1- / Bron: TronicDe afgeleide
Het bepalen van de afgeleide van een zekere functie wordt differentiëren genoemd. Differentiëren is een van de belangrijke wiskundige operatie's die in de wetenschap worden gebruikt. Het is ongeveer gelijktijdig uitgevonden door Newton en Leibniz in de 17-de eeuw.De afgeleide functie geeft informatie over de steilheid van de raaklijn aan de functie in een bepaald punt, hoe snel stijgt de grafiek in punt P(x, y)? (zie figuur 1)
De raaklijn door punt P maakt een hoek met de x-as. Voor het bepalen van deze hoek moeten we de toename in de y-richting delen op de toename in de x-richting: Δy / Δx.
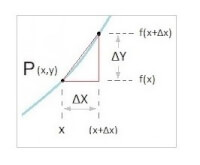 -fig 2-
-fig 2-Newton : Δx < elk getal dat je kunt bedenken
/ Bron: Tronic
- Δy = f(x+Δx) - f(x)
..., we kunnen nu Δx als een oneindig klein stukje toename voorstellen, ...
- door de limiet te nemen van Δx-->0
- zo ontstaat de afgeleide f '(x) = lim Δx-->0 (Δy / Δx)
De afgeleide van de functie f(x) wordt ook wel aangeduid als
- f '(x)
- df(x)/dx
- d/dx [f(x)]
Een bekende afgeleide in de natuurkunde is snelheid. De plaatsfunctie kan geschreven worden als functie van de tijd t: x(t), differentiëren naar de tijd t levert de snelheid v(t):
> v(t) = x '(t) = dx(t)/dt.
De versnelling is op zijn beurt weer de afgeleide van de snelheid: a(t) = dv(t)/dt. Een andere bekende afgeleide is elektrische stroom: i(t) = dQ/dt, de elektrische stroom is de hoeveelheid lading die per seconde passeert.
Bekende afgeleide's
Voor het bepalen van de afgeleide functie's f '(x) gelden een aantal rekenregels die we kunnen toepassen op bijna elke f(x).Daarnaast zijn de afgeleide's van de meest voorkomende functie's bekend.
(het dakje ^ betekent tot de macht, a is een constante).
| f (x) | f '(x) | niet gedefinieerd voor |
|---|---|---|
| a | 0 | |
| ax | a | |
| 1/x | -1/x² | (x=0) |
| x^a | a x^(a-1) | |
| ln(x) | 1/x | (x=0) |
| loga x | 1/(ln(a) x) | (x=0) |
| sin(x) | cos(x) | |
| cos(x) | -sin(x) | |
| tan(x) | 1/cos²(x) | (x=1/2π, 3/2π) |
| e^x | e^x | |
| a^x | ln(a) a^x |
Rekenregels
Voor het differentiëren van samengestelde functie's gelden de volgende rekenregels:lineariteit
- [a f(x)] ' = a f '(x)
- [af(x) + bg(x)] ' = af '(x) + bg'(x)
- [f(x) g(x)] ' = f '(x) g(x) + g'(x) f(x)
- [f(x)/g(x)] ' = (f '(x)g(x) - g'(x) f(x)) / g²(x) (...nat-tan/n ²= (noemer afgeleide teller - teller afgeleide noemer)/noemer²)
- [f (g(x))] ' = f '(g(x)) g '(x)
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: tronic
- LA Reichard (auteur Getal en Ruimte)
- Afbeelding bron 1: Tronic
- Afbeelding bron 2: Tronic
Reacties
Vangampelaere Jonny, 13-10-2019
Wat is de afgeleide van x tot de x-de macht?
Reactie infoteur, 22-10-2019
Jonny, goede vraag, dat is
x^x(1+ln(x)) (zie youtube voor de afleiding).
Henk Schuulten, 26-03-2017
Geachte heer,
Graag wilde ik iets leren over differentieren en integreren. Ik vond een stukje uitleg in uw artikel en ben benieuwd of er eeenvoudige en duidelijke lectuur is over deze onderwerpen.
Uw artikel gaf mij al wel enig inzicht en mijn dank hiervoor. Mijn stelling is, je bent nooit te oud om te leren en dat pas ik met mijn 81 jr. ook toe.
Met vriendelijke groet,
Henk Schulten
Reactie infoteur, 27-03-2017
Beste mijnheer Schulten,
Dank voor uw reactie, ik raad u de reeks boeken "Getal en Ruimte" aan, studieboeken voor scholieren, u moet dan even uitzoeken in welk deel het onderwerp differentieren behandeld wordt.
Met vriendelijke groet,
Tronic
Laatste update: 19-07-2018
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 4