Waarom krachten afnemen met het kwadraat van de afstand

De natuurkunde kent een aantal wetten waarin de sterkte van een kracht omgekeerd evenredig is aan het kwadraat van de afstand waarover die kracht wordt uitgeoefend. Er bestaat een tamelijk eenvoudige geometrische verklaring voor dit feit. Deze wordt besproken waarbij ook wordt ingegaan op twee belangrijke aannames die nodig zijn wil de geometrische verklaring geldig zijn. De kern is dat kracht energie is en dat de krachten afnemen naarmate de ruimte die ze bestrijken groter wordt.

Figuur 1: De tweede wet van Newton

Afstand en zwaartekracht

Twee objecten met een massa trekken elkaar aan. Dat feit is de zwaartekracht gaan heten. De sterkte van die aantrekkende kracht is volgens de tweede wet van Newton omgekeerd evenredig met het kwadraat van de afstand tussen beide objecten. De volledige formule is gegeven in figuur 1 (klik voor een vergroting). Daar is te lezen hoe zwaartekracht en afstand precies samenhangen. Daar is ook te lezen, maar dit terzijde, dat de zwaartekracht een zeer zwakke kracht is; de constante G is absurd klein, een feit dat al voor veel hoofdbrekens heeft gezorgd. Hoe het ook zij, het specifieke verband tussen kracht en afstand is talloze malen getoetst en geldig gebleken. Opvallend is dat dit verband tussen afstand en kracht niet alleen voor de zwaartekracht opgaat. Een groot aantal andere wetten uit de natuurkunde hebben deze eigenschap ook. De wet van Coulomb die beschrijft hoe elektrisch geladen objecten elkaar aantrekken, is daarvan een sprekend voorbeeld. De vraag ligt nu voor de hand: waarom bestaat deze relatie tussen kracht en afstand?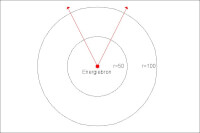

Figuur 2: De verdeling van energie

Een geometrische verklaring

Voor de beantwoording van deze vraag kijken we eerst naar een energiebron. Het maakt niet uit of die energie gezien wordt als een kracht of zelfs als een lichtbron. Al deze interpretaties leiden tot hetzelfde resultaat. In figuur 2 is de rode bol in het midden de energiebron. Deze zendt energie in alle richtingen uit en in elke richting precies evenveel. De energie reist in alle richtingen met dezelfde snelheid en dus zal het na een tijdje zich bevinden precies op de omtrek van de binnenste cirkel. Na nog een tijdje hebben de energie-stralen de buitenste cirkel bereikt. De crux is dat het steeds gaat om dezelfde hoeveelheid energie of licht die over een steeds grotere omtrek verdeeld moet worden. Deze constatering is voldoende om het inverse verband tussen kracht (of energie) en afstand af te leiden.

De omtrek van de een cirkel wordt gegeven door O = π r² waarin r uiteraard de straal is. De hoeveelheid energie die de rode bol in het begin heeft kan aangeduid worden met E. Als E verdeeld over de binnenste cirkel zal elk punt van de cirkel dus slechts een deel ervan "ontvangen". De energie per punt op de omtrek volgt dan uit:

E/O = E/(π r²)

De buitenste cirkel heeft een straal die precies twee keer zo groot is als die van de binnenste cirkel. De omtrek ervan is dus gelijk aan O = π (2r)² = 4π r² . De omtrek van de buitenste cirkel is vier maal zo groot als de omtrek van de binnenste cirkel. Elk punt op de buitenste cirkel ontvangt dus 4 maal minder energie dan elk punt op de binnenste cirkel. En dit terwijl de afstand van de buitenste cirkel slechts 2 maal zo groot is. Als nu de straal n maal zo groot wordt, dan leert dezelfde redenering dat de omtrek n² maal zo groot worden. Dat betekent op zijn beurt dat de energie per punt n² maal zo klein wordt.

Dit is precies de reden waarom er zo vaak een inverse relatie tussen bestaat tussen kracht (energie) en het kwadraat van de afstand waarover het werkt. Wat hier met de redelijk vage term energie is aangeduid kan elke willekeurige krachtbron representeren. Telkens wanneer een constante hoeveelheid van “iets” door de ruimte reist en over een groter oppervlak verdeeld wordt is er sprake van een inverse kwadratisch verband tussen kracht en afstand. Zwaartekracht, althans volgens een aantal gangbare theorieën, wordt overgebracht door deeltjes die gravitonen heten. Deze reizen door de ruimte en het aantal deeltjes blijft constant. De bovenstaande redering geldt dus ook voor de zwaartekracht.

Drie dimensies

In het voorbeeld is gewerkt met een cirkel, dus met een twee-dimensionale figuur. De werkelijk is uiteraard drie-dimensionaal. In plaats van cirkels hadden er bollen gebruikt moeten worden. Zo lijkt het misschien, maar het is lood om oud ijzer. In drie dimensies gaat het niet om de omtrekt maar om de oppervlakte. Welnu, ook de oppervlakte van een bol is evenredig met het kwadraat van de straal ervan. Om precies te zijn, de oppervlakte O van een bol wordt gegeven door O = 4π r². Er verandert dus geen spat aan de bovenstaande redenering. Zouden we in werelden leven van hogere dimensies, zelfs dan zou er nog sprake zijn van hetzelfde verband tussen kracht en afstand.

De homogeniteit van de ruimte

Het tekenen van een cirkel om een energiebron heen lijkt een voor de hand liggende zaak. Dat is het in zekere zijn ook, maar toch worden op zo'n moment een aantal belangrijke aannames gedaan. Deze zijn in het bovenstaande al min of meer impliciet aangeduid. De eerste aanname is dat de signalen (of deeltjes of golven of wat dan ook) in alle richtingen even snel bewegen. Zouden de stralen in horizontale richting sneller reizen dan die in verticale richting, dan moet de cirkel vervangen worden door een ellips. Dan verdwijnt ook de eenvoudige relatie tussen kracht en afstand. Dat toch met cirkels en bollen gewerkt kan worden, betekent dat de ruimte in alle richtingen dezelfde is. Dat is de aanname van de homogeniteit van de ruimte, een aanname die de hele natuurkunde doordrenkt en eigenlijk altijd maar weer geldig blijkt te zijn.

Eindige snelheid

De tweede aanname is dat de snelheid van de signalen eindig is. Ook hier blijkt de tijd een grote rol te spelen in de fundamenten van de natuurkunde. Dat de snelheid waarmee, onder andere, de zwaartekracht zich verspreid eindig is, is best een opvallende aanname omdat de grote Newton zelf veronderstelde dat de zwaartekracht direct en onmiddellijk werkt, hoe goot de afstand ook. De zwaartekracht plant zich dus voort met een oneindige snelheid voortplanten. Maar, als de snelheid oneindig is, dan is de energie E van de bol langs elke lijn van uitzending overal en direct aanwezig. Het kost immers geen tijd om een afstand af te leggen, dus is de energie overal. De energie E reist in dit geval niet, maar neemt meteen bezit van het hele universum, als een olievlek die zich op wonderbaarlijke wijze vermenigvuldigt en in no time alle oceanen bevuilt. Dat is uiteraard strijdig met de wet van behoud van energie. Een oneindige voortplantingssnelheid van de zwaartekracht kan gewoon niet, zelfs niet als Newton het tegendeel beweert. Oneindige snelheden van andere signalen als licht leiden tot soortgelijke problemen. Oneindige snelheden, hoe aantrekkelijk ze op het eerste gezicht ook lijken, zijn niks dan ellende.