Foto-elektrisch effect - theorie en voorbeelden
Licht wordt gebruikt om bepaalde dingen te zien. Zodra een schakelaar omgaat, wordt de hele ruimte verlicht. Licht schijnt immers op elk oppervlak. Toch heeft licht bepaalde eigenschappen, zoals de eigenschap om geabsorbeerd te worden. Wetenschappers hebben er in de 19e en 20e eeuw veel onderzoek naar verricht en hebben ontdekt dat licht in staat is om elektronen uit een metaalrooster te laten uittreden. Dit werd het foto-elektrisch effect genoemd en staat als beginsel van de kwantummechanica waar men de vruchten van plukt in het dagelijks leven.Kwantummechanica
In 1890 voerde Millikan een experiment uit waarin hij zeer kleine oliedruppels tussen twee geladen platen liet zweven, en hij ontdekte dat de oliedruppels bij een (discrete, gekwantiseerde) lading van (een veelvoud van) - 1,602176565 * 10-19 coulomb zweefden van de ene naar de andere plaat. Thomson voerde in datzelfde jaar een ander experiment uit waaruit bleek dat, tussen twee elektroden in een bijna compleet vacuüm op een bepaalde spanning, een stroom ging lopen. Dit was tegenstrijdig met de opvatting die heerste voor 1890: de opvatting was dat atomen neutraal geladen en ondeelbaar waren. Uit deze experimenten bleek wat anders: atomen bestonden uit een negatief geladen elektron en een ander deeltje met een grotere massa en een tegenovergestelde lading. Deze stelling werd nogmaals bevestigd in 1896, toen Becquerel het fenomeen radioactiviteit aantoonde: het spontaan uiteenvallen van grote, instabiele atomen.Het experiment
Het experiment om het foto-elektrisch effect aan te tonen werd opgezet als volgt: In een vacuüm worden twee elektroden aangesloten aan een spanningsbron (Hertz) , waarbij de kathode in het vacuüm het te onderzoeken metaal is. Op dit metaal werd monochromatisch (enkelkleurig) licht geschenen en onderzocht wat de uittree-energie is van een elektron in een bepaald metaal. Dit verschilt omdat de aantrekkingskracht van de kern op het elektron toeneemt met toenemende kernlading Z. Het foto-elektrisch effect toonde vervolgens aan dat er een stroom loopt voorbij een bepaalde golflengte licht. De uittree-energie wordt hierbij overwonnen, en bij afnemende golflengte (toenemende frequentie, dus toenemende E) zal het elektron ook sneller verplaatsen door het vacuüm. Daarbij moet het volgende in acht worden genomen: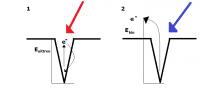
Figuur 1: diagram van uittreden van het elektron. In situatie 1 is de energie van het foton te laag om de uittree-energie te overwinnen. In situatie 2 is dat wel het geval; de resterende hoeveelheid energie is nu kinetische energie.Het licht fungeert als energiepakket met energie Efoton = h * f = (h * c) / λ, met h = 6,62606957 * 10-34 J s, c = 2,99792458 * 108 m s-1 en λ de golflengte in m, dus fotonen zijn gequantiseerd.
De kinetische energie van het elektron is gelijk aan Ekin = ½mν2 = Efoton - Euittree; met andere woorden, wanneer licht schijnt op een metaal zal de energie van het foton eerst worden gebruikt om de energieput, de uittree-energie, te overwinnen, waarbij de resterende hoeveelheid energie wordt omgezet in kinetische energie (figuur 1)
[/OLIST]
Voorbeeld 1 - Natrium
Wanneer licht met een golflengte van 200 nm op een plaat van natrium wordt geschenen in een soortgelijke opstelling als die van Hertz, wordt een stroom gemeten. 200 nm is gelijk aan een foton-energie van afgerond 1,0 * 10-18 J. De uittree-energie van een elektron in een natrium-atoom is 539 nm, wat gelijk is aan een energie van 3,7 * 10-19 J. De resterende kinetische energie is 6,3 * 10-19 J, en zodoende zal het elektron wegschieten met een snelheid van 1,18 * 106 m s-1.
Voorbeeld 2 - Ijzer
IJzer heeft een uittree-energie van 4,5 eV. Wanneer er uv-licht op ijzer wordt geschenen, schiet er een elektron weg met een snelheid van 6,3 * 105 m s-1. De golflengte van dit licht kan berekend worden door de kinetische energie die volgt uit de snelheid op te tellen bij de uittree-energie van ijzer. Dit is gelijk aan 9,01 * 10-19 J. Omrekenen met de formule Efoton = (h * c) / λ geeft een golflengte van 2,20 * 10-7 m, oftewel 220 nm.
