Het onzekerheidsprincipe
 Het wetenschappelijk determinisme was aan het begin van de 19e eeuw algemeen aanvaard onder wetenschappers. Men ging ervan uit dat er een klein aantal wetten moest bestaan dat alles in het heelal kon voorspellen wanneer de totale toestand van het heelal op een gegeven tijdstip bekend was. Werner Heisenberg ontdekte dat dit nooit het geval kan zijn. In 1926 formuleerde hij het onzekerheidsprincipe: de huidige toestand van een systeem kan nooit precies gemeten worden.
Het wetenschappelijk determinisme was aan het begin van de 19e eeuw algemeen aanvaard onder wetenschappers. Men ging ervan uit dat er een klein aantal wetten moest bestaan dat alles in het heelal kon voorspellen wanneer de totale toestand van het heelal op een gegeven tijdstip bekend was. Werner Heisenberg ontdekte dat dit nooit het geval kan zijn. In 1926 formuleerde hij het onzekerheidsprincipe: de huidige toestand van een systeem kan nooit precies gemeten worden.Determinisme
Aan het begin van de 19e eeuw heerste er groot enthousiasme over de juistheid van de theorieën die Newton ontdekt had. De voorspellingen die de theorie van de zwaartekracht deed, bleken te kloppen; het was dus een succesvolle theorie. Dit leidde ertoe dat de Franse geleerde Laplace veronderstelde dat het heelal volkomen deterministisch was. Dit betekent dat alles wat er in het heelal gebeurt, voorspeld kan worden met een aantal vaste wetten. Hiervoor moet men wel de totale begintoestand van het heelal op een zeker tijdstip weten.Vallende appel
We nemen als voorbeeld de vallende appel uit de boom. Stel een appel hangt op 5 meter hoogte in een boom en dreigt te gaan vallen. De begintoestand van dit systeem is bekend, we weten namelijk:
- de hoogte s = 5 meter
- op aarde bedraagt de valversnelling g = 9,81 m/s²
Voor de relatie tussen verplaatsing, tijd, en versnelling geldt: s = 1/2g t2, dus:
- 5 = 1/2 * 9,81 * t2
- t = 1,01 seconde
De appel zal er 1,01 seconde over doen om de grond te bereiken. Op soortgelijke wijze kon met Newtons zwaartekrachtwetten de snelheid en verplaatsing van de planeten in ons zonnestelsel berekend worden. Hiervoor was nodig: kennis van de begintoestand van het zonnestelsel en de zwaartekrachtwetten.
Laplace
Vanwege het succes van deze wetten concludeerde Laplace dat niet alleen de planeten en voorwerpen onderhevig waren aan vaste wetten, maar dat alles in het heelal deterministisch was. Met andere woorden: er zouden wetten bestaan die alles – inclusief het menselijk gedrag – verklaarden en konden voorspellen. Deze opvatting werd gemeengoed onder natuurkundigen in de eerste jaren van de 19e eeuw.
Twijfel
Aan het begin van de 20e eeuw maakte de natuurkunde een revolutie door. Er werd steeds meer ontdekt over de structuur en het gedrag van atomen. De Deense geleerde Niels Bohr had een standaardmodel voor een atoom opgesteld. Dit kwam erop neer dat elektronen in banen om een atoomkern heen draaiden. De elektronen konden alleen in bepaalde vaste banen om de kern draaien. Wanneer een elektron van baan wisselde, ging dit gepaard met het opnemen of afstoten van energie die precies even groot was als het energieverschil tussen twee banen.
Dit model was een grote stap voorwaarts, maar had nog wel tekortkomingen. Van elektronen was bekend dat ze zich soms als deeltje en soms als golf gedroegen. Het golfkarakter van elektronen was niet opgenomen in het model.
Nieuw atoommodel
Daarom besloot de geleerde Werner Heisenberg een nieuw atoommodel te ontwikkelen. Hij probeerde het dualistische (golf/deeltje) karakter van elektronen te omzeilen. Hij negeerde de banen van elektronen en richtte zich vooral op de energie die elektronen afstaan of opnemen.
Onzekerheidsprincipe
Heisenberg stuitte op een probleem toen hij rivaliserende modellen en vergelijkingen bestudeerde die het gedrag van deeltjes op subatomaire schaal moesten beschrijven. Wanneer hij tegelijkertijd de positie en de snelheid van een deeltje wilde berekenen was de uitkomst onzeker of onnauwkeurig.Hij meende dat deze onzekerheid niet het gevolg was van een tekortkoming in de vergelijkingen maar van de aard van de subatomaire wereld. In 1926 publiceerde Heisenberg de theorie van het onzekerheidsprincipe. Deze theorie stelt dat men óf de snelheid óf de positie van een subatomair deeltje op een bepaald moment kan kennen (meten) maar niet allebei tegelijkertijd. De reden hiervoor is dat door de manier van snelheid meten de positiemeting van het deeltje onzeker wordt. Andersom geldt dat het meten van de positie van het deeltje, de snelheid van het deeltje beïnvloedt en de snelheidsmeting onnauwkeurig maakt.
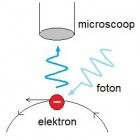
De aard van deeltjes op subatomair niveau is dat elk deeltje een bijbehorende golf heeft. Om een deeltje te kunnen zien moeten we licht toevoeren; licht is een golf.
Positiemeting beïnvloedt snelheid
Hoe korter de golflengte van het gebruikte licht, des te nauwkeuriger kunnen we de positie van het deeltje bepalen. Bij een (relatief) korte golflengte hoort een hogere frequentie en een hogere energie. Deze hogere energie van een lichtfoton dat op het deeltje valt, zal de snelheid van het deeltje meer beïnvloeden dan een lagere energie.
Snelheidsmeting beïnvloedt positie
Omgekeerd: wanneer we licht met een (relatief) langere golflengte gebruiken zal de snelheid minder beïnvloed worden en dus nauwkeuriger te meten zijn. Maar een langere golflengte brengt een onnauwkeuriger positie-meting met zich mee.
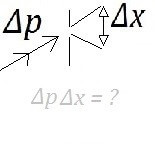 Bron: Tronic
Bron: TronicStel we vangen de (door licht beschenen) deeltjes op; via een gat ter grootte Δx arriveren de deeltjes op een observatiescherm. We kunnen de variatie in afstand waarop de deeltjes op het scherm terechtkomen uitdrukken als functie van de variatie in de impuls Δp (p = mv, dus Δp = mΔv). De relatie tussen de onzekerheid in positie en snelheid werd door Heisenberg vastgesteld als:
- Δx * Δp = h/4π
Hierin is h een constante; h wordt ook wel de constante van Planck genoemd (=6,63*10-34). Is de onzekerheid in de positie Δx groot, dan is de onzekerheid in de snelheid (Δp) klein, want h is constant. Andersom geldt hetzelfde.
Het onzekerheidsprincipe van Heisenberg is een fundamentele eigenschap van de wereld. In onze zichtbare wereld merken we er maar weinig van; de onbepaaldheidsfactor is zeer klein. In de wereld van het atoom echter is de onzekerheid extreem belangrijk. In feite betekent het principe dat het heelal dus niet deterministisch kan zijn; we kunnen namelijk nooit de begintoestand exact meten.