Thermodynamica eerste hoofdwet
 De thermodynamica bestudeert de wisselwerking tussen grote aantallen deeltjes. Met de eerste hoofdwet, of 'de wet van behoud van energie', hebben we dagelijks te maken. Er kan geen energie uit niets ontstaan en er gaat nooit energie verloren. De wamte-energie die in een liter benzine zit, wordt omgezet in bewegingsenergie van een auto. Niet alle oorspronkelijke energie uit de liter benzine zal bewegingsenergie worden, een gedeelte zal worden omgezet in warmte. De totale hoeveelheid energie blijft echter gelijk.
De thermodynamica bestudeert de wisselwerking tussen grote aantallen deeltjes. Met de eerste hoofdwet, of 'de wet van behoud van energie', hebben we dagelijks te maken. Er kan geen energie uit niets ontstaan en er gaat nooit energie verloren. De wamte-energie die in een liter benzine zit, wordt omgezet in bewegingsenergie van een auto. Niet alle oorspronkelijke energie uit de liter benzine zal bewegingsenergie worden, een gedeelte zal worden omgezet in warmte. De totale hoeveelheid energie blijft echter gelijk.
Thermodynamica
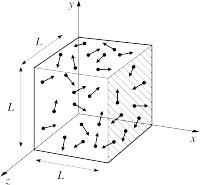 -fig 1- Thermodynamisch systeem
-fig 1- Thermodynamisch systeem/ Bron: Socratic.org
De deeltjes, moleculen en atomen, vormen samen bijvoorbeeld een vaste stof, vloeistof, of een gas. We bekijken van een stuk materiaal (dat begrensd is) bijvoorbeeld eigenschappen zoals:
- druk
- temperatuur
- volume
Statistische gemiddelden
Er wordt geen model gemaakt van de individuele deeltjes waaruit een systeem bestaat, maar van eigenschappen die statistische gemiddelden zijn over het gedrag van een zeer groot aantal deeltjes.Deeltjes kunnen zowel potentiële energie (opgeslagen energie) als kinetische energie (bewegingsenergie) bezitten. Het systeem waarvan de deeltjes bestudeerd worden noemen we een thermodynamisch systeem. Onder een thermodynamisch systeem wordt verstaan:
- Een systeem dat via een grens(vlak) mechanische arbeid en warmte kan uitwisselen met de omgeving.
Eerste hoofdwet = wet van behoud van energie
De eerste hoofdwet van de thermodynamica zegt het volgende:- Energie kan niet verloren gaan, en energie kan niet uit het niets ontstaan
Nulde hoofdwet
Het blijkt dat grootheden in een thermodynamisch systeem, zoals temperatuur, druk, volume en uitwendige arbeid allemaal met elkaar samenhangen. Daarnaast heeft een systeem een inwendige energie en zullen magnetische en elektrische velden ook een invloed hebben op de individuele deeltjes. Hoe kan men hiervoor een model opstellen?Er is een houvast nodig om te kunnen rekenen met zoveel invloeden. Daarom heeft men de nulde hoofdwet opgesteld. Deze wet beschrijft het begrip temperatuur, men zegt:
- De temperatuur is een toestandsfunctie
Dit betekent dat de temperatuur een functie is die altijd tot dezelfde uitkomst komt, ongeacht welke variabelen men hiervoor moet veranderen. Naast het toevoeren van warmte zijn er meer methodes om de temperatuur van een gas te laten stijgen. Door een gas samen te persen, zullen de moleculen harder of meer op elkaar botsen, waardoor de temperatuur zal toenemen.
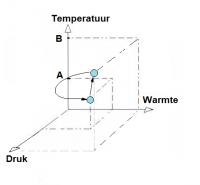 -fig 2-
-fig 2-Temperatuur is een toestandsfunctie
- de druk van het gas verhogen en daarna het gas verwarmen,
- of andersom: eerst verwarmen en dan samenpersen.
De huidige waarde van de temperatuur wordt niet beinvloed door de volgorde van veranderen van druk en warmte(toevoer) en ook niet door de vorige waarde van de temperatuur. Een andere belangrijke eigenschap van een toestandsfunctie is dat wanneer men terug wil naar de oorspronkelijke toestand, de omgekeerde route van actie's moet worden uitgevoerd.
Wiskundig gezegd: de kringintegraal is nul. De kringintegraal van de temperatuurfunctie -zie figuur 2- schrijven we als:
- ∫ T(p,Q) dpdQ (A->B) + ∫ T(p,Q) dpdQ (B->A) = 0
Hierbij staat T voor de temperatuur, p voor druk, en Q voor de toegevoerde warmte. De lijn van A naar B beeldt af hoe de druk (p)- en warmte (Q)-verandering tot temperatuur B leidt. Om terug te gaan van punt B naar punt A, kunnen we een willekeurige route kiezen.
Eerste hoofdwet
Het kenmerk van een thermodynamisch systeem is dat het na verloop van tijd een evenwichtstoestand zal bereiken. In deze toestand veranderen de grootheden niet meer van waarde; deze evenwichtstoestand wordt vastgelegd in de toestandsfunctie zoals de hierboven beschreven functie voor de temperatuur.De toegevoerde warmte en de verrichte arbeid kunnen niet worden vastgelegd in een toestandsfunctie. De waarde van deze grootheden wordt bepaald door de weg naar de evenwichtstoestand toe, niet door de evenwichtstoestand zelf. We kunnen dus de warmte en arbeid berekenen als de weg tussen de doorlopen evenwichtstoestanden bekend is.
Wet van behoud van energie
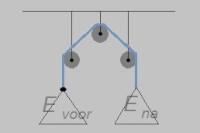 -fig 3-
-fig 3-E voor = E na
- E = T + V
hierin staan
- T voor de totale hoeveelheid kinetische energie (bewegingsenergie)
- V voor de totale hoeveelheid potentiële energie
Wanneer we een voetbal recht omhoog schieten, dan zal de bal in eerste instantie veel kinetische energie hebben. Naarmate de bal een grotere hoogte bereikt, neem zijn snelheid af, maar de hoeveelheid potentiële energie neemt toe. Op het hoogste punt is de kinetische energie van de bal nul, en de potentiële energie maximaal. Vervolgens valt de bal omlaag; de snelheid van de bal neemt steeds toe, en de potentiële energie van de bal neemt steeds meer af. Uiteindelijk valt de bal op de grond en op dat moment is de kinetische energie maximaal en de potentiële energie weer nul.
Is de snelheid waarmee de bal weggeschoten is (E voor) even groot als de snelheid waarmee de bal weer op de grond komt? Nee, de bal heeft onderweg een gedeelte van de kinetische energie afgestaan aan de luchtdeeltjes waarmee het in contact is gekomen. Dit afstaan van kinetische energie is wrijving van de bal met de lucht; de lucht rondom de bal wordt iets warmer. Het lijkt dus alsof er energie verloren is gegaan, maar er is een gedeelte van de oorspronkelijke energie omgezet in iets anders.
- E voor = T voor + V voor
- E na = T na + afgestane warmte + V na
- E na = E voor
Formulevorm
De wet van behoud van energie wordt in de thermodynamica geformuleerd in de eerste hoofdwet:- ΔE = ∑Q - ∑W
Hierin staat E voor de toename van de hoeveelheid inwendige energie, Q voor de toegevoerde warmte, en W voor de verrichte arbeid. Deze wet geldt voor een gesloten systeem met onveranderlijke samenstelling. Men kan ook zeggen: De toename van de inwendige energie + op de omgeving verrichte arbeid = hoeveelheid toegevoerde warmte
Er is altijd sprake van een bepaalde hoeveelheid energie, die telkens wordt omgezet in een andere vorm. Zelfs de ontdekking van Einstein dat massa en energie in elkaar over kunnen gaan, heeft geen invloed op de wet van behoud van energie. De totale hoeveelheid energie van een geïsoleerd systeem zal bestaan uit de kinetische energie, potentiële energie, thermische energie, restenergie, etc.
Dieselmotor
De berekening van de totale verrichte arbeid en van de afgestane/toegevoerde warmte wordt uitgevoerd door de processen die van evenwichtstoestand naar evenwichtstoestand lopen te bekijken. Bij een dieselmotor kunnen we niet helemaal de kring rond maken, maar met een beetje redeneren komen we een heel eind.Voor een ideaal gas geldt: pV = nRT (de zogenaamde gaswet). Hierin staan p voor de druk, V voor het volume, en T voor de temperatuur van het gas. De waarde van n en R zijn voor een bepaalde hoeveelheid gas constant. Een andere schrijfwijze is p(V) = nRT / V.
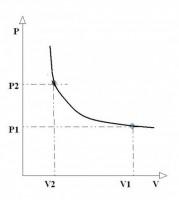 -fig 4-
-fig 4-pV kromme
De arbeid die een gas verricht ten opzichte van zijn omgeving, is eenvoudig te berekenen: W = ∫ F dl. De grootheid druk afgeleid van kracht en oppervlak: p = F/S, met S is het oppervlak waarop de kracht drukt. Het volume van het gas bestaat uit het oppervlak (vd dwarsdoorsnede) van de cilinder maal de lengte l van het luchtkanaal: V= S * l, waarbij S = constant. De lucht heeft nu negatieve uitwendige arbeid verricht:
- Arbeid = ∫ F dl = ∫ p(V) dv (V1-->V2) = ∫ nRT1 / V dV (V1-->V2) = nRT1 ln(V) | (V1-->V2) = nRT1 [ln(V1)-ln(V2)]
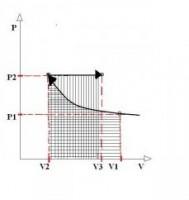 -fig 5-
-fig 5-Arbeid
- ∫p(V) dv (V2-->V3) = ∫ p2 dv (V2-->V3) = nRT2 / V3 (V3-V2) = nRT2 (1-V2/V3)
Kringproces
Op deze wijze kunnen we bij elk proces dat van toestand A naar toestand B verloopt de verrichte arbeid berekenen. Wanneer de processen die doorlopen worden uiteindelijk weer bij de begintoestand uitkomen dan spreekt men van een kringproces. Om de bijbehorende verrichte arbeid te vinden moeten we de kringintegraal uitrekenen. Stel een kringproces doorloopt achtereenvolgens de toestanden A, B, C, D, en A. Dan zal de totaal verrichte arbeid zijn:- W = ∮ p dV = ∫ p dV (A-->B) + ∫ p dV (B-->C) + ∫ p dV (C-->D) + ∫ p dV (D-->A)
De wet van behoud van energie gaat op voor een gesloten systeem met onveranderlijke samenstelling. Daarom is het niet juist om deze wet toe te passen voor het gas in de cilinder in een dieselmotor, want nadat de zuiger in de motor omlaag bewogen heeft, zal het ge-explodeerde gasmengsel de cilinder worden uitgeblazen. Het is dan dus geen gesloten systeem meer, want er wordt materie uitgewisseld (via een grensvlak) met de omgeving.
Het is wel duidelijk dat in een dieselmotor geen enkele vorm van energie verloren gaat, het verandert alleen van vorm. De toegevoerde warmte verandert in uitwendige arbeid (een draaiende motor) en nieuwe warmte door wrijving.
© 2019 - 2025 Tronic, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 William Thomson Kelvin, vastlegger van de temperatuurschaalWilliam Thomson Kelvin was op zeer jonge leeftijd al een erg intelligent persoon. Toen hij tien jaar was werd hij al toe…
William Thomson Kelvin, vastlegger van de temperatuurschaalWilliam Thomson Kelvin was op zeer jonge leeftijd al een erg intelligent persoon. Toen hij tien jaar was werd hij al toe…
 Entropie, de orde of wanorde van energieAls we om ons heen kijken dan lijkt het universum waarin we leven één groot geheel te zijn van allerlei systemen die per…
Entropie, de orde of wanorde van energieAls we om ons heen kijken dan lijkt het universum waarin we leven één groot geheel te zijn van allerlei systemen die per…
 Management: contingentiebenadering, systeembenadering en TQMDe systeembenadering is een managementtheorie waarbij men van grote afstand naar organisaties kijkt. Begrippen als 'tran…
Management: contingentiebenadering, systeembenadering en TQMDe systeembenadering is een managementtheorie waarbij men van grote afstand naar organisaties kijkt. Begrippen als 'tran…
 Berekenen van de soortelijke warmte en uitleg joulemeterAls je water wil verwarmen om bijvoorbeeld thee te zetten moet je warmte toevoeren. Heb je een fluitketel, dan wordt die…
Berekenen van de soortelijke warmte en uitleg joulemeterAls je water wil verwarmen om bijvoorbeeld thee te zetten moet je warmte toevoeren. Heb je een fluitketel, dan wordt die…
 Het onzekerheidsprincipeHet wetenschappelijk determinisme was aan het begin van de 19e eeuw algemeen aanvaard onder wetenschappers. Men ging erv…
Het onzekerheidsprincipeHet wetenschappelijk determinisme was aan het begin van de 19e eeuw algemeen aanvaard onder wetenschappers. Men ging erv…
Gerelateerde artikelen
Bronnen en referenties
- Fundamental Physics 1, Mechanics, Alonso, Finn, 1986
- Van spierkracht tot warmtedood, M.J. Sparnaay
- Afbeelding bron 1: Socratic.org
Tronic (33 artikelen)
Gepubliceerd: 22-01-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 3
Gepubliceerd: 22-01-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 3
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.