Halveringstijd en -dikte – theorie en berekening
Tijdens de Koude Oorlog nam, tezamen met de opbouw van 's werelds nucleaire arsenalen, het onderzoek naar elektromagnetische straling toe. Een effect van de nucleaire wapens was namelijk dat elektromagnetische straling vrijkwam, wat door alle materialen kan. Zodoende werd een geheel nieuwe tak van de natuurkunde geopend, waarbij de halveringstijd en vervaltrajecten van verschillende isotopen werd onderzocht. Ook werd ontdekt dat deze elektromagnetische straling een halveringsdikte heeft voor verschillende materialen. Wat is nucleaire straling, en wat houden halveringsdikten- en tijden in?Stralingssoorten
Nucleaire straling is afkomstig uit de kern (nucleus is het Latijnse woord voor kern) van een willekeurig deeltje. In de natuurwetenschappen wil een systeem een zo laag mogelijke energietoestand bereiken. Kerndeeltjes kunnen zodoende beschouwd worden als een systeem met een bepaalde hoeveelheid energie. Voor sommige kerndeeltjes is deze optimale energietoestand al bereikt: 4He is een stabiel deeltje en vertoont geen nucleair verval. Maar voor andere deeltjes, zoals een natuurlijk 13C-deeltje (halveringstijd 5730 jaar), of een synthetisch 99mTc-deeltje (halveringstijd 6 uur), worden fotonen waargenomen zodra deze moederkernen vervallen in hun dochterkernen. Dit gebeurt met verschillende soorten straling. Een zware kern, zoals 103Lr (halveringstijd 0,7 s), vervalt middels α-verval. Dit houdt in dat een 4He-deeltje wordt geëjecteerd van de moederkern, met een energie van 9,8 MeV. Een 194Os-deeltje (halveringstijd 6 jaar) vervalt volgens β--verval, waarbij een elektron en een anti-elektronneutrino worden afgestoten uit de kern. De stralingssoorten en hun energieën zijn dus verschillend voor elke kern.Radioactiviteit - de Becquerel
Radioactiviteit wordt gemeten in de hoeveelheid kernen die per seconde vervalt. De SI-eenheid voor radioactiviteit is zodoende Bq en wordt gemeten in s-1. De Becquerel (Bq) en Hertz (Hz) kunnen niet verwisselbaar worden gebruikt. De Hz is een eenheid die periodiciteit aangeeft, zoals voor de frequentie van een golf. Straling neemt, naarmate de tijd vordert, exponentieel af en is zodoende aperiodiek, en om het verschil te maken tussen periodiek en aperiodiek wordt voor een aperiodieke eenheid, zoals radioactiviteit, Bq gebruikt.Voorbeeld 1 - 7Be
Beryllium-7 heeft een atoommassa van 7,016929 u en een halveringstijd van 54 dagen. Om de radioactiviteit te berekenen gaan we uit van 1 mol beryllium-7, waarbij de constante van Avogadro NA = 6,022 141 29 * 1023 mol-1. Om de radioactiviteit te berekenen gebruiken we de volgende formule:
ABq = m/mmol * NA * ln(2)/t1/2
Gezien hier het gegeven is dat er met 1 mol beryllium-7 wordt gewerkt, is de verhouding m/mmol 1. De halveringstijd van 54 dagen moet worden omgezet naar seconden om tot de eenheid van Bq te komen, waardoor de halveringstijd 4 665 600 seconden is. Invullen geeft het volgende:
ABq = 1 * 6,022 141 29 * 1023 * ln(2)/4 665 600 = 8,95 * 1016 Bq
In een mol beryllium-7 vervallen 8,95 * 1016 deeltjes per seconde. Dit getal wordt de (radio)activiteit van een stralingsbron genoemd.
Penetratie van straling
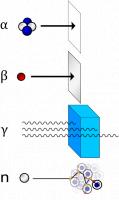Figuur 1: soorten straling / Bron: Anynobody~commonswiki, Wikimedia Commons (CC BY-SA-4.0)Halveringsdikte
De halveringsdikte van elektromagnetische straling is afhankelijk van de energie van de straling en het materiaal waardoor de straling gaat. De formule voor halveringsdikte luidt als volgt:
I(d) = I(0) * (½)d/d½,
Waarbij I(d) de (relatieve) intensiteit van de straling is op afstand d, I(0) de initiële intensiteit, d de afstand die de straling door het materiaal heeft gereisd en d½ de halveringsdikte voor elektromagnetische straling met die energie en voor dat materiaal.
Voorbeeld 2 - Lood
Als straling van 10 MeV door lood reist, is de halveringsdikte 1,23 cm. Als het lood 19 cm dik is, hoeveel van de originele straling komt dan door het lood?
Invullen geeft I(19,3) = 10 * (½)19/1,23 = 2,24 * 10-4 MeV
Lood is een excellente isolator voor elektromagnetische straling. Heel veel wanden van oude bunkers zijn zodoende gemaakt van een mengsel van cement en lood, om van de sterkte van het beton te profiteren en van de absorptie van het lood.
Voorbeeld 3 - Water
Hoeveel centimeter water is er nodig om ervoor te zorgen dat 30 % van de elektromagnetische straling met een energie van 5 MeV doorkomt?
In dit voorbeeld moet de formule herschreven worden. Hier moet namelijk de werkelijke dikte berekend worden. Dit gaat als volgt:
Gegeven:
I(d) = 0,3 I(0) = 1 d½ = 22,9 cm I(d) = I(0) * (½)d/d½
0,3 / 1 = (½)d/22,9 (invullen en omzetten)
0,5log(0,3) = d/22,9 (logaritme voor grondtal 0,5 van 0,3 nemen aan beide zijden)
22,9 * 0,5log(0,3) = d = 39,78 cm (beide zijden vermenigvuldigen met de halveringsdikte)
I(39,78) = 1 * (½)39,78/22,9 = 0,299968, oftewel 30%. Invullen met de absolute waarden geeft de absolute doorgang van energie. Dit getal gedeeld door de originele energie geeft hetzelfde percentage.
0,3 / 1 = (½)d/22,9 (invullen en omzetten)
0,5log(0,3) = d/22,9 (logaritme voor grondtal 0,5 van 0,3 nemen aan beide zijden)
22,9 * 0,5log(0,3) = d = 39,78 cm (beide zijden vermenigvuldigen met de halveringsdikte)
I(39,78) = 1 * (½)39,78/22,9 = 0,299968, oftewel 30%. Invullen met de absolute waarden geeft de absolute doorgang van energie. Dit getal gedeeld door de originele energie geeft hetzelfde percentage.
Halveringstijd
Radioactieve kernen verliezen hun potentiële energie door het uitzenden van α-, β- of γ-straling. Naarmate de tijd vordert en meer kernen dergelijke uitzendingen van stralingen veroorzaken, worden er meer dochterkernen gevormd, ook wel vervalproducten genoemd. Een radioactieve stof heeft zodoende een halveringstijd: dit is de tijd die vereist is om de helft van de radioactieve kernen te laten vervallen naar dochterkernen. Tevens is met deze kennis een heel vervaltraject op te stellen. De halveringstijd is veelal gegeven, en hiermee kan, op dezelfde manier als de halveringsdikte, gerekend worden.Voorbeeld 4 - 6He
Helium-6 is een synthetische kern en heeft een halveringstijd van 807 ms en vervalt volgens β--verval. Indien er wordt aangevangen met 10000 kernen, hoeveel kernen zijn nog 6He na 9,3 seconden?
De volgende formule geldt hier: N(t) = N(0) * (½)t/t½.
Het invullen van deze formule geeft N(9,3) = 10000 * (½)9300/807 = 3 kernen.
