Rekenen met rek, spanning en elasticiteitsmodulus van kabels
 Als je gaat vissen met een hengel lijkt het net alsof je vislijn uitrekt als je een dikke, zware vis aan je haak hebt. Hetzelfde verschijnsel kun je ook voelen als je met een groot aantal mensen tegelijkertijd een lift instapt. Je krijgt dan de gewaarwording dat de lift een beetje naar beneden zakt door het gewicht van de ingestapte mensen. Dit kun je ook zien doordat de vloer van de lift niet helemaal gelijk loopt met de liftingang. Maar hoe reken je nu uit hoeveel deze vislijn en liftkabels uitrekken?
Als je gaat vissen met een hengel lijkt het net alsof je vislijn uitrekt als je een dikke, zware vis aan je haak hebt. Hetzelfde verschijnsel kun je ook voelen als je met een groot aantal mensen tegelijkertijd een lift instapt. Je krijgt dan de gewaarwording dat de lift een beetje naar beneden zakt door het gewicht van de ingestapte mensen. Dit kun je ook zien doordat de vloer van de lift niet helemaal gelijk loopt met de liftingang. Maar hoe reken je nu uit hoeveel deze vislijn en liftkabels uitrekken?
Rek van een kabel
Om de lengteverandering van kabels/draden met uiteenlopende lengten te kunnen vergelijken maak je gebruik van de lengteverandering (uitrekking) per meter. Dit heet de rek.De formule luidt:
ԑ = Δl/l0
Waarbij:
- ԑ = de rek
- Δl = lengteverandering van de kabel in meter
- l0 = oorspronkelijke lengte van de kabel in meter
Als je naar de formule kijkt, zie je dat er bij de rek geen eenheid is gegeven. Als je waardes voor Δl en l0 ingeeft krijg je een verhoudingsgetal (ԑ). De rek wordt ook nogal eens in procenten gegeven. Als je de rek in procenten wil aangeven moet je de uitkomst van het verhoudingsgetal (ԑ) met 100% vermenigvuldigen.
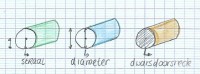 Afbeelding 1: straal, diameter en de dwarsdoorsnede
Afbeelding 1: straal, diameter en de dwarsdoorsnedeDwarsdoorsnede
Een dikke kabel breekt veel minder vlug dan een dunne kabel die gemaakt is van gelijk materiaal. Dit komt omdat bij een dikkere kabel de krachten over een groter oppervlak worden verdeeld. Deze oppervlakte heet de dwarsdoorsnede. Zie afbeelding 1 voor de straal, diameter en de dwarsdoorsnede.De oppervlakte van de dwarsdoorsnede bereken je met onderstaande formule:
A = ¼ π d2 of A = π r2
Waarbij:
- A = de oppervlakte van de dwarsdoorsnede
- π = het getal 3,14
- d = diameter
- r = straal
Spanning in een kabel
Als je dus de spanning in kabels met een verschillende dikte eerlijk wil vergelijken moet je rekening houden met de dwarsdoorsnede van de kabel.De spanning in een kabel bereken je met onderstaande formule:
σ = F/A
Waarbij:
- σ = spanning in N/m2 (wordt ook wel pascal of Pa genoemd)
- F = kracht in newton (N)
- A = oppervlakte van de dwarsdoorsnede (m2)
Als de dwarsdoorsnede groter is (de kabel is dikker) bij dezelfde kracht is de spanning σ lager.
De trekproef
Als je wil weten hoe sterk je materiaal is kun je een trekproef uitvoeren. Bij een trekproef wordt meestal een staaf in een apparaat ingespannen. Je trekt dan met deze machine met een toenemende kracht aan de uiteinden van die staaf. Op een bepaald moment knapt de staaf. De machine voor de trekproef meet de hele tijd hoeveel kracht er wordt uitgeoefend en hoeveel de staaf al is uitgerekt. Met die metingen kan een spanning-rekdiagram gemaakt worden. Afbeelding 2 bevat een weergave van het spanning-rekdiagram.Het spanning-rekdiagram
Meestal kun je drie gebieden onderscheiden in het spanning-rekdiagram. Ieder materiaal heeft een ander spanning-rekdiagram. De gebieden waarnaar worden verwezen staan in afbeelding 2.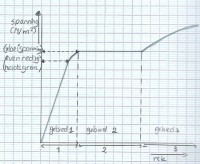 Afbeelding 2: spanning-rekdiagram
Afbeelding 2: spanning-rekdiagramGebied 1
In gebied 1 spreek je van elastische vervorming. Als je de trekkracht die je op de staaf uitoefent opheft veert de staaf weer terug en krijgt hij zijn originele lengte. In het diagram zie je dat de rechte lijn begint in de oorsprong. De spanning waarbij de lijn krom gaat lopen heet de evenredigheidsgrens. Dus tot deze spanning is bereikt mag je zeggen dat het verband tussen de spanning en de rek recht evenredig is. In dit gedeelte van de grafiek kun je dus gebruik maken van de formule van de elasticiteitsmodulus. Als de grafiek van een materiaal bij een lage spanning de evenredigheidsgrens al vlug bereikt is dit geen elastisch materiaal. Voorbeelden van elastische materialen zijn metalen. In BINAS-tabellen 8, 9 en 10 kun je de elasticiteitsmodulus van vele materialen opzoeken.Gebied 2
In gebied 2 treedt er plastische vervorming op. Het materiaal rekt steeds verder uit, terwijl de trekkracht niet noemenswaardig hoger wordt. Als je de trekkracht die je op de staaf uitoefent opheft veert de staaf NIET meer terug en krijgt hij NIET meer zijn originele lengte. Dit noem je het vloeien van het materiaal. De uitgeoefende spanning heet de vloeispanning.Gebied 3
In gebied 3 wordt de uitgeoefende kracht steeds hoger (en dus ook de spanning). Op een bepaald moment wordt de staaf op een enkele plaats veel dunner dan de rest van de staaf. Deze plaats heet een insnoering. Bij het verder verhogen van de trekkracht zal de staaf vlug breken.De elasticiteitsmodulus
De formule voor de elasticiteitsmodulus geldt in het elastische gebied (tot aan de evenredigheidsgrens). De formule luidt:E = σ/ԑ
Waarbij:
- E = elasticiteitsmodulus (N/m2 )
- σ = spanning in N/m2
- ԑ = rek (geen eenheid)
Voorbeeldopgaven
- Hoe kun je uit het spanning-rekdiagram aflezen of een materiaal stijf is? Als een materiaal stijf is betekent dit dat het materiaal niet graag elastisch vervormt. Dit kun je zien in het diagram doordat de lijn in gebied 1 erg steil loopt.
- Hoe kun je in het spanning-rekdiagram aflezen of een materiaal sterk is? Dit kun je aflezen in gebied 3. Als de spanning hoog is als de insnoering plaatsvindt betekent dit dat het materiaal sterk is.
© 2019 - 2025 Blackbeauty, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Staal, sterkte versus taaiheidVoordeel van taaiheid is dat we door vervorming de breuk, wegens overbelasting, zien aankomen, we worden gewaarschuwd. E…
Staal, sterkte versus taaiheidVoordeel van taaiheid is dat we door vervorming de breuk, wegens overbelasting, zien aankomen, we worden gewaarschuwd. E…
 De trekproef: Het spannings-rekdiagram van metalenDe trekproef is de meest uitvoerige test voor het bepalen van de mechanische eigenschappen van materialen en van metaal…
De trekproef: Het spannings-rekdiagram van metalenDe trekproef is de meest uitvoerige test voor het bepalen van de mechanische eigenschappen van materialen en van metaal…
 Hoeveel buigt een stalen ligger door?Een stalen ligger kan een bepaalde mate van doorbuiging opnemen. Het wordt bepaald door de elasticiteit en het traagheid…
Hoeveel buigt een stalen ligger door?Een stalen ligger kan een bepaalde mate van doorbuiging opnemen. Het wordt bepaald door de elasticiteit en het traagheid…
 De elasticiteitsmodulus van staalStaal is een prachtig materiaal waarmee grote gebouwen, bruggen en utiliteit mee worden gebouwd. Het is zeer praktisch i…
De elasticiteitsmodulus van staalStaal is een prachtig materiaal waarmee grote gebouwen, bruggen en utiliteit mee worden gebouwd. Het is zeer praktisch i…
 Teken het (plaats-tijd)-diagram en reken met verplaatsingAls je de beweging van een persoon (of voorwerp) wil vastleggen wil je zeker zijn waar die persoon op ieder tijdstip was…
Teken het (plaats-tijd)-diagram en reken met verplaatsingAls je de beweging van een persoon (of voorwerp) wil vastleggen wil je zeker zijn waar die persoon op ieder tijdstip was…
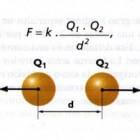 De wet van CoulombTwee elektrische ladingen kunnen een kracht F op elkaar uitoefenen. Deze kracht is vastgelegd in de wet van Coulomb. Naa…
De wet van CoulombTwee elektrische ladingen kunnen een kracht F op elkaar uitoefenen. Deze kracht is vastgelegd in de wet van Coulomb. Naa…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Clker-Free-Vector-Images, Pixabay
- Geraadpleegd op 12 februari 2019
- BINAS havo/vwo, vijfde druk. Noordhoff uitgevers tabel 18 A. ISBN 978-90-01-89380-4
- https://nl.wikipedia.org/wiki/Elasticiteitsmodulus
- https://nl.wikibooks.org/wiki/Sterkteleer/Basisbegrippen-2
- https://nl.wikipedia.org/wiki/Wet_van_Hooke
- https://nl.wikipedia.org/wiki/Treksterkte_(materiaal)
Blackbeauty (100 artikelen)
Gepubliceerd: 08-03-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 7
Gepubliceerd: 08-03-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 7
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.