De trekproef: Het spannings-rekdiagram van metalen
 De trekproef is de meest uitvoerige test voor het bepalen van de mechanische eigenschappen van materialen en van metaal in het bijzonder, zoals de treksterkte, rekgrens, taaiheid, versteviging en koudvervormbaarheid. Bij de trekproef wordt een gestandaardiseerde proefstaaf van het te onderzoeken materiaal op de kopeinden vast geklemd en op een trekbank gerekt tot het breekt. Tijdens de proef wordt het spanning-rekdiagram opgetekend, die daarna door een metaalkundige geanalyseerd wordt. De gegevens worden gebruikt door de staalleverancier om het materiaal van een attest te voorzien en om in de brochures van de staalfabrikant opgenomen te worden. De test wordt eveneens uitgevoerd om de oorzaak van het falen van een metaalconstructie te onderzoeken.
De trekproef is de meest uitvoerige test voor het bepalen van de mechanische eigenschappen van materialen en van metaal in het bijzonder, zoals de treksterkte, rekgrens, taaiheid, versteviging en koudvervormbaarheid. Bij de trekproef wordt een gestandaardiseerde proefstaaf van het te onderzoeken materiaal op de kopeinden vast geklemd en op een trekbank gerekt tot het breekt. Tijdens de proef wordt het spanning-rekdiagram opgetekend, die daarna door een metaalkundige geanalyseerd wordt. De gegevens worden gebruikt door de staalleverancier om het materiaal van een attest te voorzien en om in de brochures van de staalfabrikant opgenomen te worden. De test wordt eveneens uitgevoerd om de oorzaak van het falen van een metaalconstructie te onderzoeken. De universele trekbank, het spanning-rekdiagram wordt door de boordcomputer opgetekend / Bron: Testometric, Wikimedia Commons (CC BY-SA-3.0)
De universele trekbank, het spanning-rekdiagram wordt door de boordcomputer opgetekend / Bron: Testometric, Wikimedia Commons (CC BY-SA-3.0)Inhoud
- Inhoud
- Het spanning-rekdiagram
- Definities en symbolen van kenmerkende punten in het spanning-rekdiagram
- De wet van Hooke
- Vloeien en de vloeigrens
- De insnoering
- De poisson factor
- Berekening van de werkelijke spanning tot aan de treksterkte
- De werkelijke spanning voorbij de treksterkte tijdens het insnoeren
- Versteviging door kouddeformatie
- De trekstaaf vorm
- De verrichte arbeid tijdens de trekproef
- Toelaatbare spanning, de ontwerpspanning
- Het breukvlak als informatie bron
- Betekenis van de trekproef in de praktijk
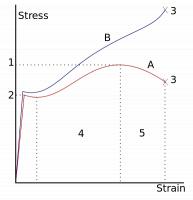 Schematische weergave van de ware spanning-rekdiagram. Onderste curve is het conventionele diagram met de spanning σ =F / Ao en de bovenste curve geeft de werkelijke spanning σw =F / A weer / Bron: Slashme / David Richfield, Wikimedia Commons (CC BY-SA-3.0)
Schematische weergave van de ware spanning-rekdiagram. Onderste curve is het conventionele diagram met de spanning σ =F / Ao en de bovenste curve geeft de werkelijke spanning σw =F / A weer / Bron: Slashme / David Richfield, Wikimedia Commons (CC BY-SA-3.0)Het spanning-rekdiagram
In het spanning-rek diagram wordt verticaal de spanning σ=P / Ao en horizontaal de lengte rek ε = ∆L / Lo = (Lo-L) / Lo uitgezet. We onderscheiden bij de trekproef vier fasen: elastische verlenging, vloeien, versteviging en insnoering. Het verband tussen de trekspanning σ en de elastische verlenging ε is recht evenredig tot aan de evenredigheidsgrens Rp (ook proportionaliteitsgrens genoemd), deze σ-ε relatie is de wet van Hooke (1678) en is te beschouwen als het begin van het metaalkundig onderzoek.Definities en symbolen van kenmerkende punten in het spanning-rekdiagram
.Treksterkte Rm
De treksterkte is de belasting per oppervlakte-eenheid gevonden door de hoogste belasting Fm tijdens de proef te delen door het oppervlak van de oorspronkelijke doorsnede Ao van de proefstaaf.
De ware breeksterkte Rw
De ware breekspanning is de belasting per oppervlakte- eenheid gevonden door de belasting ten tijde van het breken te delen door het kleinste oppervlak van de dwarsdoorsnede (insnoering) A. De spanning In het conventionele spannings- rekdiagram wordt dus berekend door de belasting te delen door de oorspronkelijke oppervlak Ao van de staaf doorsnede, maar in werkelijkheid wordt de staaf tijdens het trekken dunner, de werkelijke spanning σw is dus hoger en in de buurt van het breekpunt veel hoger. We geven dat weer in de ware spanning-rekdiagram.
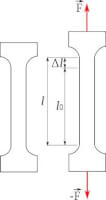 Het rekken ∆L van de trekstaaf / Bron: Cdang, Wikimedia Commons (CC BY-SA-3.0)
Het rekken ∆L van de trekstaaf / Bron: Cdang, Wikimedia Commons (CC BY-SA-3.0)De meetlengte Lo van de trekstaaf is de lengte waarvan de verlenging wordt gemeten.
De rek tijdens de proef ε
De rek ∆L / Lo = ε tijdens de trekproef is de vergroting van de meetlengte met ∆L uitgedrukt in procenten of deel van de oorspronkelijke meetlengte Lo.
De rek na het breken ε
De rek na het breken is de vergroting van de meetlengte na het breken uitgedrukt in procenten van de oorspronkelijke meetlengte Lo.
Elastische of verende rek
Elastische of verende rek is het gedeelte van de rek die bij wegnemen van de belasting terug veert naar zijn uitgangspunt.
Plastische of blijvende rek
Plastische of blijvende rek is de verlenging die na wegnemen van de belasting overblijft.
De totale rek van de belaste trekstaaf
De totale rek van de belaste staaf is de elastische rek plus de plastische rek. Pas na overschrijden van de elasticiteitsgrens is er sprake van totale rek.
De gelijkmatige rek
De gelijkmatige rek is de blijvende rek ten tijde van de hoogste spanning, daarna begint de plaatselijke (dwars)contractie(ψ).
(Dwars)Contractie (ψ)
De dwarscontractie is de vermindering van het oppervlak van de dwarsdoorsnede van de proefstaaf in procenten van het oorspronkelijke oppervlak van de dwarsdoorsnede, ook hier onderscheiden we de verende, de blijvende, de totale en de gelijkmatige(over de hele meetlengte) contractie.
Insnoering (ψ)
De insnoering is de plaatselijke contractie, d.w.z. de grootste vermindering van het oppervlak van de dwarsdoorsnede A, uitgedrukt in procenten van de oorspronkelijke oppervlak van de dwarrsdoorsnede Ao.
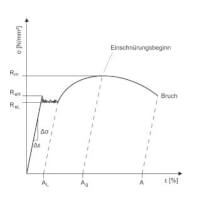 Spanning-rekdiagram met de bovenste en onderste vloeigrens / Bron: Freisein, Wikimedia Commons (CC BY-SA-3.0)
Spanning-rekdiagram met de bovenste en onderste vloeigrens / Bron: Freisein, Wikimedia Commons (CC BY-SA-3.0)De bovenste vloeigrens is de belasting per oppervlak eenheid op het moment dat deze tijdens het rekken(verlengen) niet toeneemt, gedeeld door de oorspronkelijke oppervlak van dwarsdoorsnede Ao van de trekstaaf.
Onderste vloeigrens ReL
De onderste vloeigrens is de belasting per oppervlakte eenheid van de oorspronkelijke dwarsdoorsnede Ao, als deze na het bereiken van de bovenste vloeigrens is afgenomen en daarbij de laagste waarde heeft bereikt, te delen door de oorspronkelijke oppervlak van de dwarsdoorsnede Ao.
De Hall-Petchrelatie
De Hall-Petchrelatie legt het verband tussen rekgrens en korrelgrootte van een metaal, hoe kleiner de korrel, des te sterker is het materiaal volgens benaderings formule: σ0,2 = σ0 + k /√d. Hierin is k de Hall-Petch coëfficiënt (een materiaalconstante), σo is de spanning in het materiaal op het punt dat dislocaties beginnen te bewegen, d is de gemiddelde diameter van de korrels(kristallieten) en σ0,2 is de rekgrens spanning
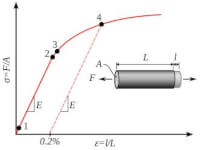 Bepaling van de 0,2 rekgrens
Bepaling van de 0,2 rekgrensTrek-rek kromme van een ductiel materiaal.
2: proportionaliteitsgrens,
3: elasticiteitsgrens,
4: 0,2%-rekgrens
/ Bron: Sigmund, Wikimedia Commons (Publiek domein)
De 0,2-rekgrens Rp is de belasting per oppervlakte eenheid gevonden door de belasting die een blijvende rek van 0,2% van de meetlengte Lo veroorzaakt te delen door het oppervlak van de oorspronkelijke doorsnede Ao. Zonder nadere aanduiding van de vloeigrens geldt voor metalen de 0,2-rekgrens. De naam rekgrens wordt gebruikt als men de beide begrippen vloeigrens en 0,2-rekgrens om praktische reden wil samenvoegen tot één begrip. De nauwkeurige rekgrens is in de praktijk niet of moeilijk te bepalen. De 0,2% rekgrens wordt bepaald door 0,2% blijvende rek op de horizontale ε as uit te zetten en een lijn evenwijdig aan modulus te trekken naar de curve, op het snijpunt met de curve lezen we dan de 0,2- rekgrens af.
De elasticiteitsgrens Re
De elasticiteitsgrens is de hoogste spanning, waarbij nog geen blijvende vervorming optreedt. De grens wordt vastgesteld door de spanning te bepalen bij een kleine percentage blijvende vervorming, bijvoorbeeld 0,04% van de meetlengte Lo.
Proportionaliteitsgrens of evenredigheidsgrens Rp
De proportionaliteitsgrens is de hoogste spanning Rp waarbij nog recht evenredigheid bestaat tussen spanning en de bijbehorende rek ε, dat is waar de wet van Hooke geldt.
De elasticiteitsmodules (E)
De elasticiteitsmodulus is de waarde gevonden door een spanning beneden de evenredigheidsgrens te delen door de bijbehorende, als deel van de meetlengte Lo uitgedrukte rek. E is de tangens van de hoek die de modulus lijn maakt met de horizontale as: E=σ / ε
De trekkromme (σ-ε)
De trekkromme is de veel gebruikte naam voor spanning-rekdiagram en is de grafische voorstelling van de betrekking tussen de vergroting van de meetlengte (rek) en de belasting (spanning). De spanning is hierbij de belasting per eenheid oppervlak van de oorspronkelijke doorsnede Ao van de trekstaaf.
De moduluslijn
De moduluslijn is het in de oorsprong beginnende rechte lijn van de trekkromme waarop de belasting(spanning) recht evenredig is aan de verlenging (rek) ε.
De wet van Hooke
De wet van Hooke luidt:
∆L = c.Lo.F / Ao
Hierin:
c = 1 / E
F / Ao = σ
∆L / Lo = ε
Uit voorgaande leiden we af:
ε = σ / E
En:
E = σ / ε
De elasticiteitsmodules E is dus in het spanning-rek diagram de tangens van de hoek die de moduluslijn maakt met horizontale ε as, F is de belasting, Lo is de oorspronkelijke trekstaaf lengte en Ao de oorspronkelijke doorsnede van de trekstaaf.∆L = c.Lo.F / Ao
Hierin:
c = 1 / E
F / Ao = σ
∆L / Lo = ε
Uit voorgaande leiden we af:
ε = σ / E
En:
E = σ / ε
Vloeien en de vloeigrens
Bij van zachtere metalen treedt vloeien op in de vorm van een vlag bij het begin van de plastisch deformatie. We onderscheiden daarbij de hoogste vloeigrens ReH en de laagste vloeigrens ReL. Bij relatief zachte materialen met een duidelijke vloeigrens neemt men om meettechnische reden de hoogste vloeigrens aan als rekgrens en niet de 0,2% rekgrens.Bij spanning toename boven de elasticiteitsgrens begint het materiaal te vloeien dat bij zacht staal beter te herkennen door de vlag, dan bij staal met hoge sterkte dat geen vlag vertoont. Vanaf dit punt is er sprake van plastische vervorming. De spanning nodig voor het vloeien heet vloeispanning σv. Bij vasthouden van de belasting blijft er verlenging optreden tot einde vloeizone. Zodra het vloeien stopt loopt de spanning op door versteviging van het metaal tot de treksterkte.
Niet voor ieder materiaal is het begin van het vloeien duidelijk. Daarom wordt de 0,2% rekgrens ingevoerd. Als de belasting na de vloeigrens wordt opgevoerd zal het materiaal plastisch vervormen. Wordt de spanning opgeheven dan verdwijnt de elastische vervorming, maar de plastische vervorming blijft bestaan. De mechanische eigenschappen van het metaal zijn veranderd, het heeft een groter elastisch gebied en een hogere rekgrens, het plastisch gebied is kleiner geworden. De versteviging begint bij de vloeigrens en loopt op tot de treksterkte, dan is de maximale spanning is bereikt.
De insnoering
De Insnoering(ψ) vindt plaats op het slanke meetgedeelte en is per definitie:
ψ = ∆A / Ao . 100%
Hierin is:
∆A = Ao-A
Dus:
ψ = (Ao-A) / Ao
ψ = ∆A / Ao . 100%
Hierin is:
∆A = Ao-A
Dus:
ψ = (Ao-A) / Ao
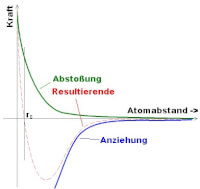 Aantrekking en afstoting tussen metaal atomen.De afstotende kracht loopt sneller op bij contractie als de aantrekkende kracht bij verlenging / Bron: Techni Tom; Franz. / Christophe Dang Ngoc Chan (cdang), Wikimedia Commons (CC BY-SA-3.0)
Aantrekking en afstoting tussen metaal atomen.De afstotende kracht loopt sneller op bij contractie als de aantrekkende kracht bij verlenging / Bron: Techni Tom; Franz. / Christophe Dang Ngoc Chan (cdang), Wikimedia Commons (CC BY-SA-3.0)De poisson factor
De drukkracht bij het samendrukken van atomen loopt sneller op dan de trekkracht bij het uit elkaar trekken van atomen. De volume vergroting door het rekken van de trekstaaf is daardoor groter dan de volume verkleining door de contractie.Bij het rekken wordt de staaf langer en dunner. Het dunner worden wordt (dwars)contractie genoemd en is bij metaallegeringen in theorie lineair verbonden met de langsrek. De verhouding tussen de dwarscontractie en de langsrek wordt uitgedrukt in de Poisson-factor v,ook Poisson-ratio genoemd.De grootte van de Poisson-factor v is per definitie de dwarscontractie gedeeld door de lengte rek:
v = εd / εL
Hierin is de lengte rek:
εL = σ / E
Na subsitutie:
εd = - v . σ / E
En:
V = εd. E / σ
Hieruit is ook af te leiden:
Poisson ratio v = ∆D / Do : ∆L / Lo
Als de volume tijdens rekken van de proefstaaf niet toeneemt maar constant is dan kunnen we berekenen dat ν= 0,5 moet zijn. Staal heeft echter een Poisson-ratio ν=0,27-0,30, bij andere metalen ligt deze tussen 0,2 en 0,5. De conclusie is dat het volume tijdens rekken wel toeneemt. Na terugveren van de trekstaaf is deze volume toename praktisch weer verdwenen en is dus elastisch van aard. De tijdelijke elastische volume toename van de trekstaaf wordt veroorzaakt doordat de drukkracht tussen de atomen bij het indrukken groter is dan de trekkracht bij het uit elkaar trekken, de dwarscontractie blijft dus achter bij de verlenging. De kracht tussen atomen als functie van de interatomaire afstand verloopt niet lineair.v = εd / εL
Hierin is de lengte rek:
εL = σ / E
Na subsitutie:
εd = - v . σ / E
En:
V = εd. E / σ
Hieruit is ook af te leiden:
Poisson ratio v = ∆D / Do : ∆L / Lo
Berekening van de werkelijke spanning tot aan de treksterkte
Uit de spanning-rek diagram volgt:
L = Lo+εLo (1)
Hieruit:
L = (1+ ε)Lo (2)
Aangezien Volume constant is geldt:
A.L = Ao.Lo (3)
Substitutie van (2) in (3):
A = Ao / (1+ ε) (4)
Per definitie geldt:
σw = F / A (5)
Hieruit na substitutie van(4) in (5):
σw = F(1+ ε) / Ao (6)
F / Ao = σo (7)
Dus:
σw = σo.(1+ ε) (8)
σo is de spanning begrepen op de oorspronkelijke doorsnede Ao in de conventionele trekkromme en σw staat voor werkelijke spanning in de ware trekkromme. Met deze formule kan de ware spanning-rek curve als functie van de verlenging ε geconstrueerd worden tot aan het punt van de treksterkte, vanuit dit punt begint de insnoering. We weten dan wat de werkelijke spanning bij de treksterkte is. De berekening is van toepassing op gelijkmatige contractie van de dwarsdoorsnede wat het geval is tot aan de treksterkte. Hierna begint de insnoering de werkelijke optredende spanningen tijdens de insnoering moet apart berekend worden.L = Lo+εLo (1)
Hieruit:
L = (1+ ε)Lo (2)
Aangezien Volume constant is geldt:
A.L = Ao.Lo (3)
Substitutie van (2) in (3):
A = Ao / (1+ ε) (4)
Per definitie geldt:
σw = F / A (5)
Hieruit na substitutie van(4) in (5):
σw = F(1+ ε) / Ao (6)
F / Ao = σo (7)
Dus:
σw = σo.(1+ ε) (8)
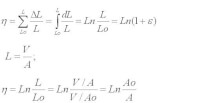 Bron: H. Koster
Bron: H. KosterDe werkelijke spanning voorbij de treksterkte tijdens het insnoeren
Voorbij het hoogste punt van de curve, dus tijdens de insnoering, geldt een andere benadering van de werkelijke spanning σw. We moeten voortdurend de belasting F delen door de kleinste doorsnede oppervlak A. De breeksterkte kan men meten door de belasting te delen door de kleinste plaatselijke doorsnede oppervlak na breuk. De rek η tijdens de contractie is η=Ln (Ao / A) waarvan de afleiding gegeven is in nevenstaande formule schema. Ook hier wordt dus ook aangenomen van de volume constant is en dus geldt dat V=L.A=Lo.Ao. De L is een fictieve lengte en Ln de natuurlijke logaritme die op elke rekenmachine te vinden is. We kunnen aan de hand van voorgaande de ware spanning-rek diagram construeren volgens afbeelding 2, van spanning en rek nul bij het begin van de proef tot de breekspanning bij de totale rek ε. Trekstaaf vorm, links een proefstaaf uit rond staf en rechts uit plaat vervaardigd. / Bron: Romary, Wikimedia Commons (CC BY-SA-3.0)
Trekstaaf vorm, links een proefstaaf uit rond staf en rechts uit plaat vervaardigd. / Bron: Romary, Wikimedia Commons (CC BY-SA-3.0)Versteviging door kouddeformatie
Tijdens trekproef stijgt de curve doordat de weerstand tegen vervorming steeds groter wordt, door het wandelen van dislocaties, een verschijnsel dat bij koudvervorming van metalen optreedt en versteviging wordt genoemd. Als we de belasting wegnemen valt spanning evenwijdig aan de rechte moduluslijn naar nul. We hebben een “nieuw” materiaal gemaakt met dezelfde elasticiteitsmodules en een beduidend hogere sterkte, echter brosser en met minder insnoering. Het oorspronkelijke materiaal wordt door het voor rekken sterker ten koste van de taaiheid en de insnoering. Het verstevigd metaal vertoont geen vloeien en vloeigrens meer. Er treedt geen versteviging op vanaf een bepaalde hoge temperatuur, de rekristalisatie temperatuur men spreekt dan van warmvervorming. Door verstevigd metaal op die temperatuur te gloeien, het zogenaamde normaliseren, krijgt het zijn oorspronkelijke eigenschappen weer terug.De trekstaaf vorm
De trekstaaf wordt in het midden dunner gedraaid om te voorkomen dat breuk in of bij de inspanning plaats vindt. Op dunne gedeelte wordt de meetlengte uitgezet, een lange meetlengte voor niet-ijzer en een korte meetlengte voor staal. In normbladen is de trekstaaf gestandaardiseerd om de uitkomsten van verschillende fabrikanten met elkaar te kunnen vergelijken. Proefstaven worden geproportioneerd genoemd als: Lo=K√So. Voor proeven in staal is volgens de EN normen de K waarde 5,65 en 5 volgens de ASME normen.De verrichte arbeid tijdens de trekproef
Arbeid die tijdens de trekproef wordt geleverd is belasting maal verlenging. De arbeid wordt weergegeven door het oppervlak tussen curve en horizontale as.Arbeid = ∫ p dL
P = σ. A
dL = Lo. Ɛ
P.dL = σ .A. L. Ɛ
Arbeid = AoLo ∫ σ dƐ
AoLo = V (volume)
Arbeid = V ∫ σ dƐ
P = σ. A
dL = Lo. Ɛ
P.dL = σ .A. L. Ɛ
Arbeid = AoLo ∫ σ dƐ
AoLo = V (volume)
Arbeid = V ∫ σ dƐ
Toelaatbare spanning, de ontwerpspanning
De te verwachten grootste spanning moet onder de 0,2 rekgrens blijven omdat anders blijvende vervorming van de constructie optreedt. Dit heet de toelaatbare spanning. De spanning in een constructie is moeilijk theoretisch te bepalen, er zijn schattingen omtrent omstandigheden zoals een storm of een zwakke plek door plaatselijke inhomogeniteit in een onderdeel, daarom werkt men met een veiligheidsfactor wegens onvoorziene omstandigheden. Men komt al gauw op een toelaatbare spanning die de helft is van de 0,2 rekgrens. Deze beschouwing geldt voor statische belasting, voor dynamische belastingen geldt een andere benadering van de toelaatbare spanning, die is afhankelijk van de soort dynamische belasting maar valt altijd lager uit dan bij een statische belasting.Ook bij hogere temperaturen wordt uiteraard gewerkt met een lagere ontwerpspanning. Constructeur en productie stellen vaak tegenstrijdige eisen aan de eigenschappen van het materiaal en moeten in onderling overleg een compromis sluiten.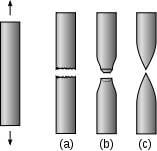 Brosse breuk links en taaie breuk rechts/ Bron : Wikipedia.org .de / wiki/ Duktilität / Bron: Sigmund, Wikimedia Commons (CC BY-SA-3.0)
Brosse breuk links en taaie breuk rechts/ Bron : Wikipedia.org .de / wiki/ Duktilität / Bron: Sigmund, Wikimedia Commons (CC BY-SA-3.0)Het breukvlak als informatie bron
Wanneer de breuk in de trekstaaf niet in het midden optreedt maar op een willekeurige plaats op de staaf wijst dat op niet homogeen materiaal, door plaatselijke verontreinigen of door oppervlakte beschadigingen, zoals krassen. Door oppervlakte beschadiging treedt kerfwerking op met een spanningsconcentratie als gevolg. Deze concentraties treden op bij scherpe overgangen in materiaaldikte en in scherpe binnenhoeken. Om dat te voorkomen past men afrondingen en meer geleidelijke overgangen toe. Is de structuur van de breuk glad en mat dan duidt dat op een fijnkorrelige structuur. Een ruwe glinsterende breuk wordt veroorzaakt door een grofkorrelige structuur. Een kratervormige breukvlak duidt op taai materiaal en een rechte vlakke breuk op hard en bros materiaal. Taai materiaal geeft een grote insnoering en bros materiaal geeft weinig insnoering.Betekenis van de trekproef in de praktijk
De eigenschappen die men uit de trekkromme leest zijn in twee groepen te verdelen:- De nadruk ligt op vormgeving en bewerkbaarheid.
- De nadruk ligt op de belastbaarheid dus op de toe te laten spanningen.
Voor goede plastische vervorming wensen we:
[OLIST]Een lage 0,2 rekgrens om de bewerkingskrachten klein te houden.
Een grote rek en grote insnoering voor een grote vervormbaarheid.
Lage treksterkte zodat weinig versteviging optreedt en de vervormingsenergie laag is. [/OLIST]
Voor metaal dat verspaand wordt wensen we:
[OLIST]Lage sterkte voor een lage verspaningskracht en langere levensduur van het gereedschap.
Het oppervlak tussen trekkromme en de horizontale ε as, dat staat voor de verspanningsenergie, zo klein mogelijk houden.
Kleine rek en insnoering zodat er geen lange taaie spanen ontstaan en een ruw werkstuk oppervlak, maar korte spanen met een glad werkstuk oppervlak. “Harde” metalen geven een gladder oppervlak dan taaie metalen. De spaan wordt bij taaie materialen als het ware “losgetrokken” van het werkstuk oppervlak.[/OLIST]