De eerste wet van Newton: statica

De statica gaat uit van lichamen in evenwicht: doordat iedere kracht die op een lichaam werkt wordt gecompenseerd door een andere kracht, wordt het lichaam niet in beweging gebracht (of blijft het met constante snelheid voortbewegen). Met behulp van de statica kan een voorspelling worden gedaan van de krachten die op een lichaam werken.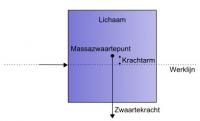

Figuur 1: lichaam, kracht en krachtarm (klik om te vergroten)

Begrippen

Een lichaam is alles waar een kracht op kan aangrijpen. Dit kan (een deel van) het menselijk lichaam zijn, maar ook bijvoorbeeld een tafel of een boom. Een kracht is de werking van een lichaam op een ander lichaam. Zo is zwaartekracht de aantrekkende kracht waarmee de aarde ervoor zorgt dat voorwerpen naar beneden vallen. De werking van een kracht wordt bepaald door de volgende aspecten: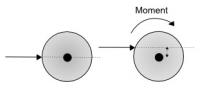

De grootte van de kracht

De richting van de kracht

Het aangrijpingspunt van de kracht

<I>Figuur 2: het effect van een krachtarm wordt duidelijk in het voorbeeld van een diskjockey. Als er tegen de plaat wordt geduwd op een rechte lijn met de draaias, zal de plaat niet gaan draaien (links). Kruist de krachtrichting de draaias niet, dan zal de plaat wel aan het draaien worden gebracht, zoals in het rechterplaatje (klik om te vergroten)</I>

Figuur 2: het effect van een krachtarm wordt duidelijk in het voorbeeld van een diskjockey. Als er tegen de plaat wordt geduwd op een rechte lijn met de draaias, zal de plaat niet gaan draaien (links). Kruist de krachtrichting de draaias niet, dan zal de plaat wel aan het draaien worden gebracht, zoals in het rechterplaatje (klik om te vergroten)

Het verlengde van de richting waarin een kracht werkt, wordt de werklijn van de kracht genoemd. Een kracht zorgt voor een roterende werking rond ieder punt van het lichaam dat niet op de werklijn ligt. Deze roterende werking noemen we het moment van de kracht, welke in de eenheid Newtonmeter (Nm) wordt weergegeven.

Moment (M) = kracht (F) * arm (d)

De arm van de kracht is de loodrechte afstand tussen de werklijn van de kracht en een punt van een lichaam. Gewoonlijk wordt hiervoor het massazwaartepunt genomen: het punt waar de resultante zwaartekracht aangrijpt. Aangenomen wordt dat de gehele massa in het zwaartepunt geconcentreerd is. Figuren 1 en 2 geven een grafisch overzicht van dit begrippenkader.

Statisch evenwicht

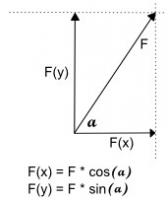Figuur 3: ontbinden van een kracht in x-richting en y-richting

Als een lichaam in evenwicht is, is de resultante van alle krachten die er op werken gelijk aan nul. Met andere woorden:

De som van alle krachten in de x-richting is nul.

De som van alle krachten in de y-richting is nul.

De som van alle momenten om een punt ‘p’ is nul.

De eerste wet van Newton wordt samengevat met de volgende evenwichtsvergelijkingen (Σ staat voor de som van de betreffende krachten of momenten):

ΣF(x) = 0

ΣF(y) = 0

ΣM = 0

Stel dat de x-richting als horizontaal wordt gedefinieerd, dan staat de y-richting daar haaks op (verticaal). Hoe zit het dan met krachten in schuine richting? Deze worden ontbonden in de x- en y-richting. Figuur 3 geeft weer hoe het ontbinden van een kracht in zijn werk gaat.

Vrij lichaam diagram

Als meerdere krachten op een lichaam aangrijpen, en dan vooral als er sprake is van krachtarmen groter dan nul, dan zorgt het uittekenen van de situatie voor een helder beeld ervan, zodat de juiste berekeningen kunnen worden gedaan. We spreken van een zogenaamd vrij lichaam diagram (VLD): alleen het essentiële wordt getekend, door het lichaam te isoleren van zijn omgeving. Gaat het bijvoorbeeld om het berekenen van de krachten die op de onderarm werken, dan kan de rest van het lichaam buiten beschouwing worden gelaten. In het VLD worden ook alle krachten en momenten die op het geïsoleerde lichaam werken getekend. Door middel van een coördinatenstelsel wordt aangegeven welke richtingen corresponderen met de x- en y-richting en welke draairichting als positief wordt bestempeld.

Bij het isoleren van een lichaam moet wel worden gerealiseerd dat de omgeving waaruit het lichaam afkomstig is, mogelijk wel krachten erop uitoefent. Stel dat de onderarm het lichaam van interesse is, dan moeten ook de krachten en het moment die worden veroorzaakt door de bovenarm worden aangegeven. Deze grijpen aan op de doorsnede waar de onderarm van de bovenarm is gescheiden, en worden dan ook snedegrootheden genoemd. Ze representeren onder andere de invloed van botten en spieren.

Voorbeeld
Ter illustratie is hier uitgewerkt hoe groot het moment is dat de bovenarm moet opwekken om een gewicht vast te kunnen houden in de hand. De volgende gegevens zijn bekend:

Het vastgehouden gewicht (b) bedraagt 2 kg.

De onderarm (a) wordt in horizontale positie gehouden en weegt 2 kg.

De lengte van de onderarm is 40 cm; het massazwaartepunt bevindt zich op 18 cm gemeten vanaf de elleboog.

De gravitatieversnelling (g) bedraagt 10 m/s².

De volgende evenwichtsvergelijkingen zijn van toepassing:

ΣF(x) = 0

ΣF(y) = 0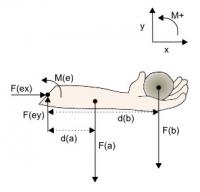

Figuur 4: VLD van de onderarm (klik om te vergroten)

ΣM = 0

Uitwerking van de evenwichtsvergelijkingen:

Aangezien er geen kracht in x-richting is waarvoor de snedegrootheden moeten compenseren, is F(ex) gelijk aan nul.

De krachten in de negatieve y-richting bedragen 20 N (2 kg * 10 m/s² voor de zwaartekracht van het vastgehouden gewicht, F(b), en nog eens 20 N voor dat van het gewicht van de onderarm, F(a). Om dit te compenseren, levert de bovenarm dus een kracht van 40 N in de positieve y-richting; dit is F(ey).

De zwaartekracht op het vastgehouden gewicht levert een moment, M(b), van -20*0,40 = -8 Nm ten opzichte van het draaipunt (de elleboog). De zwaartekracht op de onderarm geeft een moment, M(a), van -20*0,18 = -3,6 Nm. Opgeteld is dit -11,6 Nm. Het moment M(e) staat dus gelijk aan 11,6 Nm.

Het resulterende moment in de elleboog kan worden geïnterpreteerd als de kracht die de biceps levert om te voorkomen dat het rechtsdraaiende moment dat de onderarm door de zwaartekracht naar beneden kantelt.

De andere wetten

Bovenstaand voorbeeld heeft betrekking op een lichaam in rust. De wet van de statica geldt echter voor lichamen die met constante snelheid bewegen: zou er een resultante kracht op werken, dan zou er een versnelling, vertraging of verandering van bewegingsrichting optreden. Als er sprake is van een resultante kracht, dan is de tweede wet van Newton van toepassing.