Bindingsenergie van atoomkernen
De kern van een atoom is lichter dan de som van de massa's van de deeltjes waaruit deze bestaat. De verklaring voor dit verlies van massa ligt in de bindingsenergie in de kern; het kost namelijk energie om de deeltjes in de kern vrij te maken. In dit artikel wordt duidelijk wat de bindingsenergie van een kern precies is, en welke factoren invloed hebben op de grootte ervan.Allereerst raad ik de lezers die niet goed bekend zijn met de opbouw van een atoom(kern) aan om eerst dit artikel over atoomkernen door te lezen. Om te zorgen dat iedereen dit artikel beter kan volgen zullen daarnaast alle termen worden toegelicht bij de eerste keer dat ze worden gebruikt.
Inhoud
Bindingsenergie van een kern
MassadefectEen deuteron (de kern van een deuteriumatoom) bestaat uit een proton en een neutron, met een massa van respectievelijk mp=1,007825 u en mn=1,008665 u. De massa van een deuteron is md=2,014102 u, wat 0,002388 u kleiner is dan de som van de massa's (mp+mn) van de twee nucleonen (verzamelnaam voor protonen en neutronen) in het deuteron. Dit verschil in massa wordt het massadefect, of de bindingsenergie (Wb) van de kern genoemd. De bindingsenergie is de hoeveelheid energie die moet worden toegevoegd om de nucleonen in een kern te scheiden.
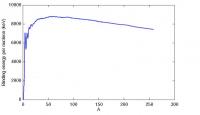 Figuur 1: Gemiddelde bindingsenergie per nucleon t.o.v. het aantal nucleonen per nuclide.
Figuur 1: Gemiddelde bindingsenergie per nucleon t.o.v. het aantal nucleonen per nuclide.Gemiddelde bindingsenergie per nucleon
Een goede maat voor de stabiliteit van een atoomkern is de gemiddelde bindingsenergie per nucleon. Deze energie wordt gevonden door simpelweg de totale bindsingsenergie van een nuclide (atoomkern) te delen door het aantal nucleonen (A) waaruit deze bestaat: Wb/A.
Factoren die meespelen bij de grootte van de bindingsenergie
Verzadiging van de kernkrachtenIn figuur 1 is te zien dat de bindingsenergie per nucleon (voorbij A=10) vrijwel constant is; het verschil is maximaal 10%. Dit komt omdat de nucleonen in een kern alleen met zijn directe buren in wisselwerking treedt. Om deze reden is de bindingsenergie per nucleon bij kernen die weinig deeltjes bevatten zo laag; de nucleonen hebben hier simpelweg minder buren. Maar in nucliden met meer dan tien nucleonen is het maximaal aantal 'buren' per nucleon bereikt, waardoor de gemiddelde bindingsenergie per nucleon niet verder toeneemt. Dit effect wordt verzadiging van de kernkrachten genoemd. Omdat de bindingsenergie per nucleon vrij constant is, is de totale bindingsenergie als volgt te benaderen:
Wb=a1A. Waarin a1 een constante is.
Het kernoppervlak
Nucliden met meer dan tien nucleonen hebben per kerndeeltje het maximale aantal 'buren' ongeveer bereikt, maar de nucleonen aan het oppervlak van de kern (het kernoppervlak), zullen natuurlijk minder buren hebben dan de nucleonen dieper in de kern. Naarmate het kernoppervlak van een nuclide groter wordt, zal dit oppervlakte-effect ook groter worden. Er zal dus een correctieterm moeten worden toegevoegd aan de vergelijking voor de totale bindingsenergie.
Het kernoppervlak (Ok) van een nuclide is evenredig met het kwadraat van de straal (Ok=4πr2) en de straal is weer evenredig met de derdemachtswortel van het aantal nucleonen in de kern (dit wordt toegelicht in het artikel over atoomkernen). Hierdoor is het kernoppervlak dus evenredig met het kwadraat van de derdemachtswortel van het aantal nucleonen in de kern. Met deze informatie kan de correctieterm voor de totale bindingsenergie worden gedefinieerd:
Wb=a1A - a2A⅔. Waarin a2 een constante is.
Coulombafstoting tussen de protonen
De protonen binnen een nuclide zijn positief geladen en stoten elkaar dus af. Dit verminderd de bindingsenergie van de kern, waardoor er nog een correctieterm moet worden toegevoegd. De coulombenergie in een nuclide is evenredig met het kwadraat van het aantal protonen (Z) en omgekeerd evenredig met de kernstraal. De vergelijking voor de totale bindingsenergie wordt nu:
Wb=a1A - a2A⅔ - a3Z2A-⅓. Waarin a3 een constante is.
De asymmetrieterm
Een volgende correctieterm die moet worden aangebracht is een nogal complex effect dat wordt veroorzaakt door het verschil tussen het aantal neutronen (N) en het aantal protonen (Z) in een atoomkern. Het zogenaamde uitsluitingsprincipe van Pauli stelt dat twee identieke fermionen (deeltjes met een halftallige spin, zoals protonen, neutronen en elektronen) nooit dezelfde kwantumtoestand mogen bezetten. Dit principe is bijvoorbeeld de reden dat twee elektronen nooit dezelfde baan in een atoom bezetten.
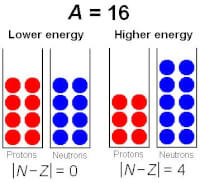 Figuur 2: Illustratie van de asymmetrieterm / Bron: CyborgTosser, Wikimedia Commons (CC BY-SA-3.0)
Figuur 2: Illustratie van de asymmetrieterm / Bron: CyborgTosser, Wikimedia Commons (CC BY-SA-3.0)De totale energie is dus het laagst als precies de helft van de nucleonen in een kern neutronen zijn, en de andere helft protonen. De correctieterm die hieruit volgt is erg ingewikkeld af te leiden, maar men kan aan tonen dat deze neerkomt op: a4(N - Z)2A-1. Waarin a4 een constante is. De vergelijking voor de totale bindingsenergie wordt nu:
Wb=a1A - a2A⅔ - a3Z2A-⅓ - a4(N - Z)2A-1.
De waarden van de constanten in de vergelijking voor de bindingsenergie
Experimentele waarden van WbDe waarden van de constanten a1, a2, a3 en a4 zijn geen getallen die theoretisch gevonden zijn. De waarden zijn verkregen door ze af te stemmen op de experimenteel bepaalde waarden van de bindingsenergieën (Wb) van de tot nu toe bekende nucliden. De waarden (uitgedrukt in MeV, oftewel mega elektronvolt) zijn momenteel op:
| a1 | 15,760 MeV |
| a2 | 17,810 MeV |
| a3 | 0,711 MeV |
| a4 | 23,702 MeV |