Normaal verdeelde variabelen en waarom ze vaak voorkomen
De normaalverdeling is alomtegenwoordig in de sociale en economische wetenschappen. Het laat een zeer zuinige en dus aantrekkelijke karakterisering toe van veel empirisch vergaarde data omdat het volledig bepaald wordt door slechts twee parameters: het gemiddelde en de variantie. De voor de hand liggende vraag is waarom deze verdeling zowat voorkomt. De Centrale Limiet Stelling uit de statistiek geeft een mogelijk antwoord.Toevalsvariabelen
Een toevalsvariabele is een variabele die een van te voren onbekende waarde kan aannamen. Met een dobbelsteen, bijvoorbeeld, kan een van de waarden van 1 tot en met 6 gegooid worden. Pas na de worp is de waarde bekend en kan aan een toevalsvariabele, die we X mogen noemen, een waarde toegekend worden (meestal aangeduid met x). Er is dus geen toevalsvariabele zonder een experiment of procedure die er een waarde aan toekent.Het experiment of de procedure kan van alles zijn. Het gooien van een dobbelsteen is maar een voorbeeld. Het afnemen van een IQ test is een andere. Van te voren zal niet bekend zijn hoe hoog iemand scoort; pas na de test ligt de waarde vast. Nog een ander experiment kan bestaan uit het verzamelen van de inkomensgegevens van mensen uit een bepaald land. Ook hier geldt dat de toevalsvariabele die het inkomen van een persoon representeert pas ingevuld kan worden nadat de relevante gegevens verzameld zijn.
De uniforme verdeling
Hoewel de waarde van een toevalsvariabele X zelf zelden met zekerheid voorspeld kan worden, kan vaak wel iets gezegd worden over de kans waarmee een bepaalde waarde wordt gemeten of aangetroffen. Voor de dobbelsteen is dit heel eenvoudig. Elke waarde van 1 tot en met 6 heeft een kans die precies gelijk is aan 1/6. De verdeling van de kansen - of waarschijnlijkheden - is dus theoretisch bepaald en kan vervolgens vergeleken worden met de geobserveerde waarden. In figuur 1 staan bij wijze van voorbeeld de resultaten van drie van zulke experimenten. In het eerste is 20 maal met een dobbelsteen gegooid, in het tweede 200 maal en in het derde 2000 maal. Duidelijk is te zien dat naarmate er vaker gegooid wordt, de benadering tot de rode (theoretische) lijn - die een kans van 1/6 voor alle waarden weergeeft - steeds beter is.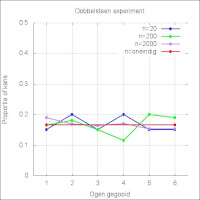
Figuur 1: Dobbelsteen experiment
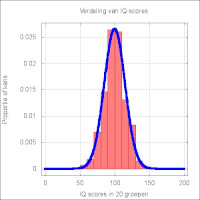Figuur 2: IQ metingen
Figuur 3: Vergelijkingen voor de normaalverdelingDe normaalverdeling
Lang niet in alle gevallen kunnen de verwachte kansen op voorhand precies bepaald worden en blijkt het pas achteraf. Als er een experiment gedaan wordt waarbij van een groot aantal mensen het IQ bepaald wordt, dan kunnen de resultaten eruit zien als in figuur 2. De rode staven geven de proportie aan van het aantal mensen dat een bepaald IQ gehaald heeft. De scores zijn hierbij in 20 groepen verdeeld die elk 10 IQ punten omvatten.Deze verdeling heeft de wat onregelmatige kenmerken die typisch zijn voor empirisch vergaarde gegevens. Maar toch is er een patroon in waar te nemen. De blauwe lijn is de normaalverdeling die normaalgesproken het beste past op zulke IQ experimenten. Een andere naam voor de normaal verdeling is "verdeling van Gauss". De verdeling uit figuur 2 heeft een gemiddelde van 100 en een variantie van 225 (dus een standaard deviatie van 15). De vergelijking van deze verdeling staat in figuur 3.
De normaalverdeling wordt hier dus gehanteerd als een model, oftewel, als een samenvatting van de gegevens. Dat slechts twee parameters nodig zijn om deze lijn te beschrijven, maakt het tot een heel zuinig en dus plezierig model voor theoretici. De normaalverdeling is heel anders dan de uniforme verdeling die het dobbelsteen experiment het beste beschrijft. Niet alle IQ scores hebben immers een even grote kans van voorkomen. De kans dat iemand een 0 of de maximale score haalt, is vele malen kleiner dan de kans op een score van 100. De score van 100 zal, door de bank genomen, het meest voorkomen, domweg omdat de IQ testen gemaakt zijn om een gemiddelde score van rond de 100 op en een standaard deviatie van rond de 15 op te leveren.
Merk verder op dat de normaalverdeling ook kansen toekent aan onmogelijke scores. Volgens de verdeling is er een (heel kleine) kans dat een score negatief is. Ook dat geeft aan dat de verdeling gezien moet worden als een benadering van de empirische data (of omgekeerd natuurlijk, het is maar hoe men er tegen aan kijkt).
Waarom de normaalverdeling zo vaak voorkomt
In principe zijn er een oneindig aantal mogelijke waarschijnlijkheidsverdelingen. De normaalverdeling is best bijzonder onder andere omdat het gemiddelde de hoogste kans van optreden heeft en omdat het symmetrisch is. De kans dat een score, zeg 10 punten links van het gemiddelde ligt is precies even groot als de kans dat de score 10 punten rechts van het gemiddelde ligt. Een wat meer verborgen eigenschap is dat de verdeling aan alle waarden van de toevalsvariabele X een kans toekent; het is een continue verdeling zonder boven- en ondergrens.De normaalverdeling komt in de praktijk van het onderzoek zo frequent voor dat de vraag voor de hand ligt waarom dat zo is. Een van de antwoorden ligt verborgen in een belangrijke stelling in de statistiek: de Centrale Limiet Stelling (CLS). CLS stelt, grofweg, dat wanneer een toevalsvariabele de som is van een groot aantal andere toevalsvariabelen, dat het dan al snel de normaalverdeling zal volgen.
Iets preciezer: laat Y(1) tot en met Y(n) een aantal toevalsvariabelen zijn die niet van elkaar afhankelijk zijn. Dat wil zeggen dat de waarde van, zeg Y(i) niet afhankelijk is van de waarde van Y(j) voor alle i en j die niet aan elkaar gelijk zijn en kleiner dan of gelijk zijn aan n. Als elk van de toevalsvariabelen Y(i) een eigen kansverdeling heeft met een gemiddelde en een variantie die niet oneindig zijn, dan zal de toevalsvariabele X = Y(1) + ... + Y(n) bij benadering normaal verdeeld zijn, tenminste wanneer n groot genoeg is. Het is hierbij niet nodig dat de toevalsvariabelen Y(i) allemaal dezelfde verdeling hebben. De Y(3) kan uniform verdeeld zijn en Y(12) kan zelf normaal verdeeld zijn of welke andere verdeling ook hebben. De enige eis dus dat elk van deze verdelingen een eindig gemiddelde en een eindige variantie hebben. Een verdere eis is nog dat de som Y(1) + ... + Y(n) niet (vrijwel) volledig door een van de Y termen bepaald worden. Het effect van de Y termen moet, met andere woorden, van eenzelfde orde van grootte zijn.
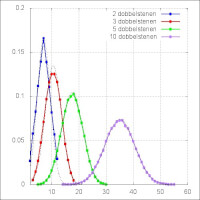Figuur 4: Voorbeeld van de werking van de centrale limiet stellingNeem aan dat de Y(i) allemaal dobbelstenen zijn en dus met een kans van 1/6 een waarden van 1 tot en met 6 kunnen aannemen. Laat X de som van de waarden van de dobbelstenen zijn. Wanneer een dobbelsteen 2 maal gegooid moet worden om een waarde af te lezen, dan liggen de mogelijke waarden dus tussen 2 (tweemaal een 1 gegooid) en 12 (tweemaal een zes gegooid), bij 100 keer gooien is het minimum gelijk aan 100 en het maximum gelijk aan 600. In figuur 4 zijn de resultaten van een aantal van zulke experiment weergegeven, waarbij steeds het aantal dobbelstenen toeneemt. Duidelijk is te zien dat wanneer het aantal dobbelstenen toeneemt de verdeling steeds meer op een normaalverdeling lijkt. Bij twee dobbelstenen ontstaat nog een figuur die het meeste weg heeft van een tent, maar al bij drie dobbelstenen worden de contouren van een normaalverdeling zichtbaar. Dat was op basis van CLS dus ook te verwachten, zij het wel met de opmerking dat, althans bij uniform verdeelde variabelen, er niet eens zo heel veel variabelen gesommeerd hoeven te worden.
Voor de analytici: het gemiddelde en de variantie van de normaalverdelingen in deze figuur hangen beide af van het gemiddelde en de variantie van de gesommeerde uniform verdeelde variabelen. Het gooien van een dobbelsteen leidt tot een gemiddelde van 3,5 en een variantie van 35/12. Worden n dobbelstenen gegooid, dan is zowel het gemiddelde als de variantie n maal zo groot. Dit is terug te vinden in figuur 4 waar de verdeling steeds breder wordt. In figuur 4 zijn met zwarte stippellijnen ook de best passende normaalverdeling getekend. Wanneer de gesommeerde toevalsvariabelen een andere dan een uniforme verdeling volgen, dan zal de benadering in de regel wat slechter zijn. Het aantal benodigde Y termen zal dan groter moeten zijn wil een normaalverdeling resulteren.
