Statistiek de normale verdeling
De functie die voor continue kansvariabelen de kans als functie f van een zekere uitkomst x weergeeft, noemt men de kansdichtheid f(x). Kansen zijn te berekenen door het oppervlak -'via' wiskundige integratie- onder de grafiek te bepalen. Een speciale kansdichtheid is de normale verdeling; het blijkt dat in de natuur en bij series experimenten de gemeten gegevens vaak volgens deze verdeling te beschrijven zijn. Bij de normale verdeling vallen het gemiddelde, de mediaan, en de modus samen in een punt.Normale verdeling
De normale verdeling is de meest gebruikte kansverdeling in de statistiek. Uit verzamelde praktijkgegevens blijkt dat tal van variabelen een verdeling hebben die qua vorm overeenkomt met de normale verdeling. Dit verschijnsel komen we vooral tegen in situaties waar een serie metingen verricht wordt bij hetzelfde fenomeen. Een reeks metingen die verricht wordt blijkt vaak een hoeveelheid waarnemingen of uitkomsten op te leveren die te beschrijven zijn met de wiskundige functie 'normaal verdeelde frequentieverdeling'.Wanneer een reeks metingen in de natuur gedaan wordt, bijvoorbeeld het gewicht van een bepaalde groep personen, blijken de uitkomsten eveneens vaak te beschrijven volgens dezelfde wiskundige functie, daarnaast wordt het gebruik van de normale verdeling vaak gefundeerd door gevolgtrekkingen uit de theoretische statistiek.
Een belangrijke stelling uit de kansrekening is de centrale limietstelling. Deze stelling zegt dat de gemiddelden van grote series waarnemingen zich als een normaal verdeelde variabele gaan gedragen als de steekproefomvang naar oneindig gaat. Wanneer een kansvariabele zelf niet normaal verdeeld is, kan men vanwege de centrale limietstelling, toch de normale verdeling gebruiken voor het gemiddelde van een steekproef.
- de normale verdeling is een functie van een continue variabele x, de dichtheidsfunctie f(x)
- oppervlaktes onder de grafiek van f(x) geven de kansen aan
De dichtheidsfunctie f (x) van de normale verdeling is:
f(x) = 1 / (σ√2π) exp ( -1/2 [ (x-μ) / σ ] ² )
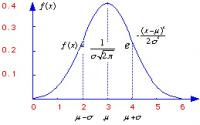-fig 1-(klik voor vergroting) / Bron: Tronic
- de verwachtingswaarde μ-- geeft aan waar de gemiddelde uitkomst ligt
- de standaarddeviatie σ -- geeft aan in hoeverre de curve breed of spits is
De top van kansdichtheidsfunctie ligt bij (x = μ), dit typeert een normale verdeling, de gemiddelde waarde van alle uitkomsten komt het vaakst voor in de meting.
Wanneer de grafiek breed is - grote σ - wijken alle uitkomsten meer af van het gemiddelde. Bij een spitse grafiek - kleine σ - is de afwijking minder. Er is een grote familie van normale verdelingen; de keuze van μ en σ bepaalt de grootte van het gemiddelde en de vorm van de curve. De normale verdeling is een symmetrische functie (rond het gemiddelde), en heeft één top.
Een variabele x die normaal verdeeld is met verwachtingswaarde en standaarddeviatie noteren we als volgt:
- x ˜ N ( μ, σ )
Zomaar een integraal berekenen van een zekere kans is niet eenvoudig. Daarom is de tabel van de standaardnormale verdeling ingevoerd.
Standaardnormale verdeling
Bij gegeven μ en σ ligt de curve van de normale verdeling vast. De kansen kunnen dan als oppervlaktes onder de grafiek berekend worden. Het is niet eenvoudig om deze integralen zomaar voor willekeurige kansen te berekenen. Daarom heeft men een andere methode ontwikkeld: via tabellen kan men de kansen voor uitkomsten gemakkelijk opzoeken / aflezen. Voor de normale verdeling heeft men een tabel geconstrueerd met - μ = 0 en σ = 1 -. Dit noemt men ook wel de standaardnormale verdeling.Stel de kansvariabele z is standaardnormaal verdeeld. Dan geldt:
- z ˜ N ( μ=0, σ=1 )
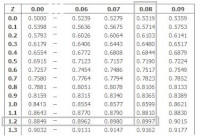-fig 2- / Bron: TronicKlik op het plaatje om de tabel te kunnen lezen. Voor het aflezen van de tabelwaarden kunnen we een zekere handigheid ontwikkelen. We weten dat het totale oppervlak onder de grafiek gelijk is aan 1. Daarnaast is de grafiek symmetrisch. Met deze feiten in het achterhoofd kunnen we alle oppervlakken onder de grafiek berekenen.
Wanneer we bijvoorbeeld willen weten hoe groot de kans op z ≥ 1.28 = P(z ≥ 1.28), dan doen we het volgende: Zoek in de tabel in de linker kolom 1.2 op. De bijbehorende rij is dit getal tot de 1e decimaal. Zoek dan in de tabel in de bovenste rij 0.08 op. De bijbehorende kolom is dit getal in honderdsten. Daar waar de rij en kolom elkaar kruisen staat het antwoord: P(z ≥ 1.28) = 0.8997.
Dus de linkerkolom geeft het getal tot de 1e decimaal, en de bovenste rij geeft de 2e decimaal (honderdsten). De kans op de uitkomst wordt gevonden door de bijbehorende rij en kolom te kruisen.
Voorbeeld 1
P(z ≥ 1.21) ? Opzoeken links 1.2; opzoeken boven 0.01. Kruisen levert : P(z ≥ 1.21) = 0.1131
Voorbeeld 2
P(0.34 < z < 1.57) ? Om deze kans te berekenen moet deze kans geschreven worden als een uitdrukking die in de tabel af te lezen moet zijn. Er geldt P( z > 0.34) = P(0.34 < z < 1.57) + P( z > 1.57), dus
P(0.34 < z < 1.57) = P( z > 0.34) - P( z > 1.57)
Aflezen in de tabel levert : P( z > 0.34) - P( z > 1.57) = (1-0.6331) - 0.0582 = 0.3669 - 0.0582 = 0.3087.
Parameters in kansverdelingen
Veel gebruikte parameters in de statistiek zijn:- verwachtingswaarde μ-- geeft aan waar de gemiddelde uitkomst ligt
- standaarddeviatie σ -- geeft aan hoeveel de metingen afwijken van de verwachtingswaarde
- mediaan -- het middelste getal van de metingen
- modus -- de gemeten waarde die het vaakst voorkomt
Bij de normale verdeling vallen μ, de mediaan, en de modus samen in een punt. De kansdichtheidsfunctie is volledig symmetrisch voor de lijn (x= μ). Er zijn verschillende functie's in gebruik bij het oplossen van statistische vraagstukken, kansdichtheidfunctie's kunnen ook asymmetrisch zijn.
