Statistiek - Centrummaten en de normale verdeling
In de statistiek worden centrummaten gebruikt om de centrale tendentie aan te geven. Er zijn verschillende maten om iets te zeggen over het midden van de verdeling. Ook kan dit op verschillende manieren worden weergegeven. Welke centrummaten zijn er en hoe lees je een normale verdeling?Centrummaten – modus
Zoals gezegd zeggen centrummaten iets over het midden, op wat voor manier dan ook. De modus doet dit door te tellen welk getal (of categorie) het meeste voorkomt. Dit kan bijvoorbeeld over cijfers die voor een toets gehaald zijn, over welke beroepsgroep het meeste voorkomt of over welke klasse het meeste voorkomt. Dit laatste wordt een modale klasse genoemd (bijvoorbeeld de leeftijdscategorie 45 – 55 jaar komt het meeste voor in bedrijf X). Tevens kunnen er meer dan één modus zijn: dit wordt een bimodale of multimodale verdeling genoemd.Centrummaten – mediaan
De mediaan vertelt welk getal, na rangschikking, in het midden staat. Dit kan alleen als het meetniveau minimaal ordinaal is, anders is er immers geen rangorde in de kenmerken. Het simpelste voorbeeld bestaat uit cijfers: stel, een klas met vijf kinderen krijgen 3 – 5 – 9 – 6 – 7 op hun toets. Dit zet je op volgorde (3 – 5 – 6 – 7 – 9) en haalt hier het middelste getal uit (6). Bij een even aantal antwoorden neem je de twee middelste getallen en deel je door twee.De mediaan is ten opzichte van het gemiddelde veel minder gevoelig voor uitschieters (of extremen) en daardoor soms een betere maat om aan te geven wat er in het midden wordt gedaan. Hier wordt een voorbeeld van gegeven onder het kopje ‘centrummaten – modus, mediaan en gemiddelde’.
Centrummaten – gemiddelde
Het gemiddelde is wat iedereen zou krijgen als het eerlijk verdeeld werd. Het wordt uitgerekend door alle getallen bij elkaar op te tellen en vervolgens te delen door het aantal getallen dat je hebt. Hiervoor is het dus nodig dat de variabele op minimaal scale niveau (interval of rationiveau) gemeten is. Het kan hier bijvoorbeeld gaan om euro’s of lengte.Centrummaten – modus, mediaan en gemiddelde
Hoe verhouden de modus, mediaan en gemiddelde zich met elkaar? Stel dat er gekeken wordt naar telefonische uitgaven in euro’s. Een onderzoek laat het volgende beeld zien (voor het gemak alvast op volgorde gezet):- Nummer 1: € 5
- Nummer 2: € 7,50
- Nummer 3: € 11
- Nummer 4: € 11
- Nummer 5: € 13,50
- Nummer 6: € 17,50
- Nummer 7: € 22
- Nummer 8: € 60
- Nummer 9: € 75
De modus is hier € 11, want deze komt twee keer voor terwijl de rest slechts één keer voorkomt. De mediaan is hier van nummer 5 met € 13,50. Het gemiddelde is ongeveer € 24,70. Alhoewel de modus en mediaan dus vrij dicht bij elkaar liggen, ligt het gemiddelde hier erg van vanaf. Bovendien is duidelijk dat slechts één persoon hier dichtbij zit (nummer 7), terwijl nummer 8 en 9 er enorm vanaf liggen. Deze uitschieters maken het gemiddelde onbetrouwbaar en hier zou de mediaan als centrummaat beter zijn.
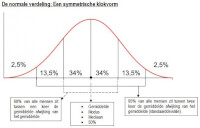
Normale verdeling
Wanneer de modus, mediaan en het gemiddelde (ongeveer) gelijk aan elkaar zijn, is de variabele gelijk verdeeld. Dit uit zich in een symmetrische klokvorm, waarbij 95% van de onderzoekseenheden zich niet dan twee keer de gemiddelde afwijking van het gemiddelde (zie plaatje) en 68% niet meer dan één keer de gemiddelde afwijking van het gemiddelde. Een normale verdeling kan bereikt worden door een grote steekproef te nemen. De normale verdeling is nodig om parametrische testen te doen (waarbij de hoogste meetniveaus nodig zijn).