Hoe kun je de uitkomst van (a+b)^n gemakkelijk bepalen?
 Formules waarbij een combinatie van a+b tot de zoveelste macht (a+b)^n moet worden berekend, kan bij een hoge n-waarde veel schrijfwerk geven. Probleem daarbij is dat men mogelijk snel het overzicht verliest, waardoor fouten in de oplossing kunnen sluipen. Om dit op te lossen kan een combinatie van het binomium van Newton met de driehoek van Pascal worden toegepast. Wat houdt deze manier van rekenen in en hoe wordt het toegepast?
Formules waarbij een combinatie van a+b tot de zoveelste macht (a+b)^n moet worden berekend, kan bij een hoge n-waarde veel schrijfwerk geven. Probleem daarbij is dat men mogelijk snel het overzicht verliest, waardoor fouten in de oplossing kunnen sluipen. Om dit op te lossen kan een combinatie van het binomium van Newton met de driehoek van Pascal worden toegepast. Wat houdt deze manier van rekenen in en hoe wordt het toegepast?
Uitkomst (a+b)^n bepalen
- Binominaalcoëfficiënt: de faculteit
- Driehoek van Pascal
- Uitschrijven van de formules (a+b)^n
- Binomium van Newton
Binominaalcoëfficiënt: de faculteit
Twee boven elkaar staande getallen tussen haakjes wordt de binominaalcoëfficiënt genoemd. Het bepaalt een noemer en deler, waarbij faculteiten worden toegepast. Een faculteit van een getal bepaalt de vermenigvuldiging van alle voorgaande getallen met dat getal, oftewel 5! = 5*4*3*2*1 = 120. De binominaalcoëfficiënt bijvoorbeeld (5/3) is gelijk aan 5!/(3!*2!) = 5*4*3*2*1/(3*2*1*2*1) = 5*4/(2*1) = 10. Deze manier van rekenen wordt binnen de driehoek van Pascal toegepast.Driehoek van Pascal
Voorgaande faculteitberekening is door Pascal toegepast binnen zijn driehoek, waarmee een wiskundige driehoek is bereikt. De uitkomst van die reeks bouwt zichzelf als volgt op:- (0/0) = 0;
- (1/0) (1/1) = 1 1;
- (2/0) (2/1) (2/2) = 1 2 1;
- (3/0) (3/1) (3/2) (3/3) = 1 3 3 1;
- (4/0) (4/1) (4/2) (4/3) (4/4) = 1 4 6 4 1;
- (5/0) (5/1) (5/2) (5/3) (5/4) (5/5) = 1 5 10 10 5 1.
- ...
Uitschrijven van de formules (a+b)^n
Wil je zelf afleiden wat de uitkomst van “tot de macht” formules is, dan dien je het uit te schrijven. Omdat (a+b) tot de n-de macht wordt herhaald, zal het met een groter wordende n-factor een toenemende formule qua lengte worden. Voor de (a+b)^n functie wordt dit als volgt gedaan:- (a+b)^0 = 1
- (a+b)^1 = 1*a + 1*b = a + b;
- (a+b)^2 = (a+b)*(a+b) = a^2 + a*b + a*b + b^2 = a^2 + 2*a*b + b^2;
- (a+b)^3 = (a+b)*(a+b)*(a+b) = a^3 + a^2*b + a*b^2 + a^2*b + a*b^2 + a^2*b + a*b^2 + b^3 = a^3 + 3*a^2*b + 3*a*b^2 + b^3;
- ...
Je ziet dat er bij een toenemende grootte van n, een lange reeks moet worden uitgeschreven. Een handige oplossing kan worden gevonden in de driehoek van Pascal. De oplossing van voorgaande formules komt overeen met de ontwikkeling van de driehoek. Oftewel via faculteit-rekenen kan voor iedere waarde van n binnen (a+b)^n worden bepaald hoe de formule eruitziet. Hoe is dit gerelateerd aan het Bionomium van Newton?
Binomium van Newton
De uitgeschreven formules hebben een exacte uitkomst, overeenkomstig de reeks van Pascal. Dit betekent dat je met een n-de macht direct de formule kunt opschrijven, door gebruik te maken van deze gegevens. Het binomium van Newton stelt daartoe het volgende:- (a+b)^n = ∑ (n/k) a^(n-k)b^k van k=0 tot k=n.
Kijken we naar voorbeelden van (a+b)^5 of (a+b)^8 dan kunnen we dat rechtstreeks als volgt uitschrijven:
- (a+b)^5 = 1*a^5+ 5*a^4*b + 10*a^3*b^2 + 10*a^2*b^3 + 5*a*b^4 + 1*b^5.
- (a+b)^8 = 1*a^8+8*a^7*b+28*a^6*b^2+56*a^5*b^3+70*a^4*b^4+56*a^3*b^5+28*a^2*b^6+8*a*b^7+1*b^8.
Voorgaande betekent dat je op een handige manier via de driehoek van Pascal formules tot de zoveelste macht handig kunt bepalen, zonder dat je veel moeten uitschrijven. Doe je voordeel door complexe formules middels voorgaande oplossing van (a+b)^n aan te pakken.
Lees verder
© 2013 - 2025 Geinformeerd, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
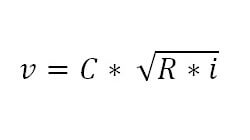 Formule van ChézyDe formule van Chézy is een formule die voortkomt uit de vloeistof leer. De zeer bekende formule is in 1775 ontwikkeld d…
Formule van ChézyDe formule van Chézy is een formule die voortkomt uit de vloeistof leer. De zeer bekende formule is in 1775 ontwikkeld d…
 Statistiek – OnderzoekTegenwoordig wordt er steeds meer onderzoek gedaan. We weten steeds meer, maar ook worden er steeds meer vragen opgeroep…
Statistiek – OnderzoekTegenwoordig wordt er steeds meer onderzoek gedaan. We weten steeds meer, maar ook worden er steeds meer vragen opgeroep…
 De getallenverzameling der gehele getallenDe getallenverzameling der gehele getallen is een verdere uitbreiding van de getallenverzameling der natuurlijke getalle…
De getallenverzameling der gehele getallenDe getallenverzameling der gehele getallen is een verdere uitbreiding van de getallenverzameling der natuurlijke getalle…
Gerelateerde artikelen
Wat is druk en hoe bereken je de druk?Wat is nu eigenlijk druk natuurkundig gezien? Hoe kun je dit op een eenvoudige manier uitrekenen? Ook in de meteorologie…
Druk omrekenen naar een andere eenheidHoe kun je druk omrekenen van bar naar PSI en vice versa? Wat is een Pascal? Hieronder staat het uitgelegd en worden een…
Gini-coëfficiënt en Gini-indexWat is de Gini-coëfficiënt in de economie en waar wordt het voor gebruikt? Zitten er veel verschillen in de Gini-coëffic…
Bronnen en referenties
- Wiskunde voor het Hoger Onderwijs deel I, R. van Asselt, C.A.G Kooten, ed, Groningen, 2002
Geinformeerd (1.029 artikelen)
Laatste update: 03-11-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Laatste update: 03-11-2016
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.