Bepalen zwaartepunt complexe figuren: statisch moment
Krijg je te maken met samengestelde oppervlakten of een combinatie van verschillende formules over meerdere intervallen (bereik en domein), dan moet voor de oppervlakbepaling een samengestelde integraal worden opgesteld. Wil je van een complex figuur het zwaartepunt oftewel het algeheel evenwichtspunt bepalen, dan moet je het statisch moment ten opzichte van x-as en y-as achterhalen. Hoe reken je dat middels integreren uit?Zwaartepunt complexe figuren uitrekenen
- Waarom oppervlakte te bepalen?
- Gebruik van een domein
- Meerdere vormen maken een geheel
- Ontleden van de deelfiguren: voorbeeld
- Interval bij neutrale lijn berekening tov y-as
- Statisch moment bepaling tov x-as
Waarom oppervlakte te bepalen?
Het totaal aan oppervlak onder een lijn kan de totale omzet van een bedrijf inhouden. Ook kan het betekenen hoeveel water per tijdseenheid door een rivier wordt afgevoerd. De formule welke de lijnvorm beschrijft legt dus vast hoeveel wordt gescoord bij een bepaalde x (tijd, afstand, ed.). Het kan daarbij uitermate nuttig zijn om het oppervlak te weten, omdat het meer vertelt over het totaalbeeld. Over welk deel wordt een oppervlak bepaald? Het antwoord hierop is afhankelijk van het interessegebied van de gebruiker. Soms wil men het ingevangen oppervlak weten tussen twee lijnen en soms is het juist om over een beperkte tijdseenheid de omzet te bepalen.Gebruik van een domein
Voorgaande betekent dat er van tijd x tot x+Δx het oppervlak onder een grafiek moet worden bepaald. Deze waarde x tot x+Δx vertegenwoordigt het domein (x-interval), waarover de opgetelde waarde van het bereik (y-resultaat) moet worden bepaald. Indien er sprake is van een samengesteld figuur dan kan over de verschillende vormen apart een domein worden vastgesteld, indien daarover de bijbehorende formules zijn bepaald. Het vormt de grondslag van meerdere integralen per figuur om zo het samengestelde oppervlak te kunnen bepalen.Meerdere vormen maken een geheel
Figuren kunnen uit enkele lijnen of samengestelde lijnen bestaan, waarmee een oppervlak wordt bepaald. Het kan bijvoorbeeld constructieve waarde hebben, omdat er krachten inwendig mee opgenomen kunnen worden. Het is dus noodzaak om het complete oppervlak tussen de verschillende domeinen te bepalen, om de opgetelde doorsnede onder de formules te kunnen vastleggen.Ontleden van de deelfiguren: voorbeeld
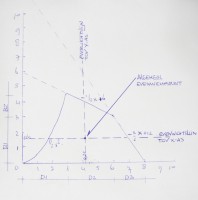Bron: Http://geinformeerd.infoteur.nl- y1 = 1/2*x^2 van 0 tot 3;
- y2 = -1/2*x+6 van 3 tot 6;
- y3 = -3/2*x+12 van 6 tot 8.
Daarbij wordt de basis gesteld op y=0 zodat de ingesloten figuur wordt verkregen. Wat zijn de afzonderlijke integralen en hoe wordt daarmee gerekend?:
- ∫D1 = ∫1/2*x^2 dx = 1/6*x^3 (0-3) = 1/6*3^3-0 = 4,5;
- ∫D2 = ∫-1/2*x+6 dx = -1/4*x^2+6*x (3-6) = -1/4*6^2+6*6 – (-1/4*3^2+6*3) = 11,25;
- ∫D3 = ∫-3/2*x+12 dx = -3/4*x^2+12*x (6-8) = -3/4*8^2+12*8 – (-3/4*6^2+12*6) = 3,0;
- totale oppervlak = 4,5 + 11,25 + 3,0 = 18,75.
Interval bij neutrale lijn berekening tov y-as
Wordt de evenwichtslijn ten opzichte van de y-as bepaald dan worden dezelfde domeinen gebruikt. Er dient over het oppervlak echter de Si waarde oftewel het momentane oppervlak worden bepaald:- Si∫D1 = ∫x*1/2*x^2 dx = ∫1/2*x^3 dx = 1/8*x^4 (0-3) = 1/8*3^4-0 = 10,13;
- Si∫D2 = ∫x*(-1/2*x+6) dx = ∫-1/2*x^2+6*x) dx = -1/6*x^3+3*x^2 (3-6) = -1/6*6^3+3*6^2 – (-1/6*3^3+3*3^2) = 49,50;
- Si∫D3 = ∫x*(-3/2*x+12) dx = ∫-3/2*x^2+12*x dx = -1/2*x^3+6*x^2 (6-8) = -1/2*8^3+6*8^2 – (-1/2*6^3+6*6^2) = 20;
- totale Si;y statisch moment ten opzichte van y-as = 10,13+49,50+20 = 79,63;
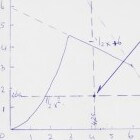
- positie evenwichtslijn: x = 79,63 / 18,75 = 4,25.
Statisch moment bepaling tov x-as
Ten opzichte van de x-as dienen de formules eerst omgezet te worden naar x waarden:- omzetting y1 naar x1: x = (2*y)^(1/2);
- omzetting y2 naar x2: y-6 = -1/2*x -> x = -2*y+12;
- omzetting y3 naar x3: y-12 = -3/2*x -> -2/3*(y-12) = x -> x = -2/3*y + 8.
Voor de Si:x bepaling gelden twee intervallen zijnde van y 0 tot 3 en van 3 tot 4,5:
- Si∫B1 = ∫y*[-2/3*y+8 – (2*y)^(1/2)] dy = ∫[-2/3*y^2+8*y – √2*y^(3/2)] dy = -2/9*y^3+4*y^2 – 2*√2/5 *y^(5/2) (0-3) = -2/9*3^3+4*3^2 – 2*√2/5 *3^(5/2) = 21,18;
- Si∫B2 = ∫y*[-2*y+12 - (2*y)^(1/2)] dy = ∫[-2*y^2 + 12*y – √2*y^(3/2)] dy = -2/3*y^3+6*y^2 – 2*√2/5 *y^(5/2) (3-4,5) = -2/3*4,5^3+6*4,5^2 – 2*√2/5 *4,5^(5/2) – (-2/3*3^3+6*3^2 – 2*√2/5 *3^(5/2)) = 9,27;
- totale Si;x statisch moment ten opzichte van x-as = 21,18+9,27 = 30,45;
- positie evenwichtslijn: y = 30,45 / 18,75 = 1,62.
Zie voor een samenvatting van voorgaande oppervlakten en evenwichtslijnen de aangegeven figuur.
