Hoe kun je een ligger op drie steunpunten doorrekenen?
Heb je een ligger op twee steunpunten dan kun je het vrij simpel en rechtlijnig uitrekenen, echter bij een ligger op driesteunpunten is dit meer complex en dient er een scharnier te worden geïntroduceerd. Het is echter de vraag wat een verstandige plek is om het aan te brengen, zodat één en ander wel concreet kan worden doorgerekend. De juiste plek van het "theoretische scharnier" is dus van essentieel belang. Op wat voor manier kan een dergelijke ligger met gelijke hart op hart afstand en constante belasting handmatig worden bepaald?Ligger op drie steunpunten uitrekenen
- Statisch onbepaalde liggers statisch bepaald maken
- Herleiding bij ligger op drie steunpunten
- Aantal scharnieren en locatie
- 25% Vuistregel afstand naast steunpunt
- Drie steunpunten ligger uitgewerkt
Statisch onbepaalde liggers statisch bepaald maken
Liggers op twee steunpunten kunnen zonder probleem worden doorgerekend. Heel anders is dit voor liggers op drie of meer steunpunten. Normaal wordt gebruik gemaakt van de totale balans waarbij verticale belasting en oplegreacties nul bedraagt. Het totaal aan alle momenten bedraagt eveneens nul. Dat houdt in dat het geheel in evenwicht is. Bij meerdere steunpunten is het statisch onbepaald, waardoor niet rechtstreeks de reacties en momenten kunnen worden bepaald. Daartoe kan men een truc toepassen, waarmee een statisch onbepaalde ligger statisch wordt. Daartoe maakt men gebruik van een scharnier. Plaats een scharnier op de locatie van een vermoedelijk momentennulpunt zodat het berekenbaar is. Waar ligt in dat geval het nulpunt voor een ligger op drie steunpunten?Herleiding bij ligger op drie steunpunten
De mate van moment- en reactiekracht verdeling wordt grotendeels bepaald door de mate van elasticiteit van een ligger. Deze factoren spelen zich af tot de vierde macht om de stijfheid te bepalen. Het traagheidsmoment wordt voor liggers uitgedrukt in mm4. De lentefactor moeten we bij een belasting dan ook naar de vierdemacht brengen om daaruit conclusies te kunnen trekken. Normaal is er sprake van: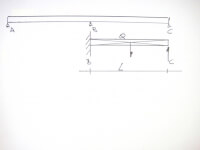
Bron: Http://geinformeerd.infoteur.nl- MB = -1/2*Q*L^2 + C*L om het moment in B te bepalen;
- SC = naar dL^2 integreren: -1/2*Q*L^2*1/4*L^2 + C*L*1/3*L^2 = -1/8*Q*L^4+1/3*C*L^3=0;
- C = A = (1/8*Q*L^4) / (1/3*Q*L^3) = 3/8*Q*L en is de grootte van de oplegreactie. Let wel dat het dwarskrachten nulpunt ook op 3/8*L van het oplegpunt is verwijderd, waarmee de plaats van het veldmaximum is bepaald;
- B:links = B:rechts = 5/8*Q*L voor de dwarskracht oftewel oplegreactie B = 10/8*Q*L.
Nu we de reactiekrachten weten kunnen we de momenten berekenen:
- MB = -1/2*Q*L^2 + 3/8*Q*L^2 = -1/8*Q*L^2 in steunpunt B;
- Mveld = 1/2*3/8*Q*L*3/8*L = 9/128*Q*L^2 gelegen op 3/8*L van steunpunt A en C.
Aantal scharnieren en locatie
Om een ligger uit te kunnen rekenen dient een scharnier aangebracht te worden op het juiste punt van een ligger. We weten het moment in B en dat de belasting Q over L constant verloopt dan kan de standaard locatie voor een scharnier worden bepaald. Daartoe geldt het volgende:- -1/8*Q*L^2 / 1/2*Q*X^2 = 0 resulteert in;
- X = 1/4*L. Oftewel voor een ligger op drie steunpunten ligt het momentennulpunt op een kwart naast het middensteunpunt. Let wel voor liggers met meerdere steunpunten bedraagt het steunpuntsmoment veelal 1/12*Q*L^2 waarmee de meest geschikte locatie uitkomt op 1/6 van de overspanning.
Is er sprake van een ligger op vier steunpunten dan moeten twee scharnieren worden geïntroduceerd en dat aantal neemt toe met een scharnier per ieder extra steunpunt.
25% Vuistregel afstand naast steunpunt
Voor doorgaande liggers wordt gewoonlijk een vuistregel toegepast voor de locatie alwaar de momentenlijn in werkelijkheid nul bedraagt. Op 25% van de overspanning naast een steunpunt zal het nulpunt liggen bij liggers op drie steunpunten (gelijke afstand en belasting). Omdat we scharnieren gaan toepassen om een statisch onbepaald systeem te benaderen dienen die scharnieren ook op die locatie te worden gesitueerd. Een scharnier zorgt ervoor dat er op dat punt geen moment heerst. Het heeft slechts de capaciteit om dwarskracht over te brengen op het volgende deel. Voor de schematisatie is het noodzakelijk om een vierde van de overspanning toe te passen omdat daarmee de werkelijke situatie zoveel als mogelijk wordt nagebootst.Drie steunpunten ligger uitgewerkt
Bron: Http://geinformeerd.infoteur.nl- reactie op de uitkraging = (5-1,25)*10/2 = 18,75 kN;
- moment steunpunt B = 18,75*6,25+1/2*1,25^2*10 = 31,25 kNm = 1/8*10*5^2;
- reactie steunpunt B = [18,75*6,25+10*6,25^2/5] / 5 = 62,50 kN = 10/8*10*5;
- reactie steunpunt A en C = 18,75 + 10*6,25 – 62,50 = 18,75 kN = 3/8*10*5;
- moment veld = 18,75*3/8*5-1/2*(3/8*5)^2*10 = 17,58 kNm = 9/128*10*5^2.
Middels voorgaande dubbele controle zie je dat de twee methoden voor het doorrekenen van de ligger op drie steunpunten op elkaar aansluiten.
