Hoe herleid je momenten bij een ligger op twee steunpunten?
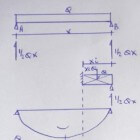 De bepaling van het representatieve of reken moment - maximale belastingstoestand voor een ligger uitgedrukt in kNm uitgerekend door belasting maal arm - is van belang om sterkte en stijfheid van materialen bij bepaalde belastingen en overspanningen te kunnen controleren. Op basis van de momenten kan een zekere materiaal met een doorsnede worden gekozen, om een voldoende sterke en stijve ligger te verkrijgen. Hoe kun je momenten herleiden zonder daartoe programmatuur toe te gebruiken?
De bepaling van het representatieve of reken moment - maximale belastingstoestand voor een ligger uitgedrukt in kNm uitgerekend door belasting maal arm - is van belang om sterkte en stijfheid van materialen bij bepaalde belastingen en overspanningen te kunnen controleren. Op basis van de momenten kan een zekere materiaal met een doorsnede worden gekozen, om een voldoende sterke en stijve ligger te verkrijgen. Hoe kun je momenten herleiden zonder daartoe programmatuur toe te gebruiken?Momenten herleiden
- Mechanica en noodzaak momenten herleiden
- Gehanteerde uitdrukkingen voor belastingen
- Gelijkmatig verdeelde belasting (1)
- Oplopende belasting (2)
- Puntlast in het midden (3)
- Gecombineerde lasten
Mechanica en noodzaak momenten herleiden
Uitgangspunt binnen de mechanica is dat er een balans moet zijn tussen de horizontale en verticale belastingen. Komt er een belasting van boven dan moet de opgetelde waarde daarvan gelijk zijn aan de opgetelde waarde van de reacties. Dit geldt voor belastingen in beide richtingen. Dat houdt in dat de constructie niet in beweging komt bij H=0 en V=0. Voor de herleiding van een oplegreactie is het van belang om kracht maal arm te nemen van de belastingen ten opzichte van de afstand tot het volgende steunpunt. Zodoende kan die reactiekracht worden bepaald en verder de momentenlijn alsmede dwarskrachtenlijn.Gehanteerde uitdrukkingen voor belastingen
Normaal drukken we een belasting uit in kilo’s en tonnen. Binnen de mechanica wordt deze waarde vermenigvuldigd met 9,81 m/s^2 (veelal wordt hiervoor 10 m/s^2 genomen voor het gemak) voor de gravitatie aantrekkingskracht om zo de waarde Newton oftewel kN (1000 N) te verkrijgen. De belasting kan per strekkende meter oftewel kN/m of als puntlast oftewel kN worden aangegeven. Die belasting komt op een ligger met lengte x te staan.Gelijkmatig verdeelde belasting (1)
 Bron: Http://geinformeerd.infoteur.nl
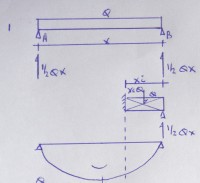
Bron: Http://geinformeerd.infoteur.nl- M = 0 in punt A en dus geldt 0,5*Q*x^2 – B*x =0;
- oftewel reactiekracht in B= 0,5*Q*x^2/x = 0,5*Q*x en dat is exact de helft van de totale gelijkmatig verdeelde belasting.
Op basis van deze gegevens kan zowel in het midden van de ligger (maximaal moment) als op andere willekeurige plekken het moment worden uitgerekend. Stel een punt op de ligger met xi van steunpunt B:
- in dat punt op afstand xi is het moment xi*0,5*Q*x-xi*Q*0,5*xi = 0,5*Q*xi*(x-xi). Het antwoord in deze bedraagt nul indien xi = 0 of als xi = x. Het maximaliseert als xi de halve afstand van x heeft bereikt oftewel 0,5*Q*0,5*x*(x-0,5*x)= 0,125*Q*x^2.
Oplopende belasting (2)
 Bron: Http://geinformeerd.infoteur.nl
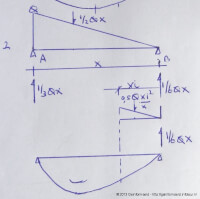
Bron: Http://geinformeerd.infoteur.nl- M = 0 in punt A en dus geldt 1/3*x*0,5*Q*x – B*x = 0;
- daarmee is de reactiekracht in B = 1/3*x*0,5*Q*x/x = 1/3*0,5*Q*x = 1/6*Q*x;
- oftewel de reactiekracht in A bedraagt (3/6-1/6)*Q*x = 1/3*Q*x.
Het moment in punt xi gedraagt zich dus anders als bij een gelijkmatig verdeelde belasting, omdat het totaal aan belastingen en reacties minder is. Er geldt het volgende:
- in xi bedraagt het moment xi*1/6*Q*x – 1/3*xi*0,5*Q*xi^2/x = 1/6*xi*Q*(x-xi^2/x). Vullen we het aangrijppunt in op 2/3*x van steunpunt B resulteert de formule in Q*(1/9*x^2-4/81*x^2) = 1/9*Q*x^2*(1-4/9) = 5/81*Q*x^2 als maximum moment.
Puntlast in het midden (3)
 Bron: Http://geinformeerd.infoteur.nl
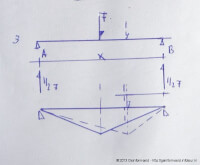
Bron: Http://geinformeerd.infoteur.nl- Moment op xi = xi*0,5*F en maximaliseert op een halve afstand = 0,5*x*0,5*F = 0,25*x*F.