Gelijkmatig verdeelde belasting: oppervlakte last op liggers

Indien stalen liggers of betonbalken worden toegepast, dienen deze te worden berekend op het eigen gewicht tezamen met het erop komende gewicht. Vloer- en wandlasten dienen adequaat te worden afgevoerd naar de oplegging, zodat een veilige, sterke en voldoende stijve opening wordt gerealiseerd. Wat houdt binnen de berekening de gelijkmatig verdeelde belasting in, zodat de juiste ligger kan worden bepaald?

Gelijkmatig verdeelde belasting

• Gewicht uit een gebouw
• Permanent versus variabel
• Vertalen belasting naar Q-last

Gewicht uit een gebouw

Voor het ontwerp van liggers en balken dient alle opgetelde belasting van boven mee te worden genomen. Het primaire uitgangspunt voor constructieve berekeningen is, dat lasten op constructies van boven naar beneden worden uitgerekend. Oftewel de complete constructie is reeds doorgerekend, zodat de belasting op het onderste constructiedeel geheel bekend is. Daarbij kan het om verschillende belastingscombinaties gaan, bestaande uit de volgende belastingstypen.

Puntlasten

Vanuit een gebouw kunnen wanden als lijnlast en als puntlast geconcentreerd voorkomen. Ook kolommen uit bovengelegen verdiepingen kunnen als last op de ligger of het meegenomen vloerdeel terechtkomen. Die concentratie aan lasten dient goed te worden opgevangen en via voldoende sterkte en stijfheid van zowel de vloer als balk te worden afgevoerd.

Continu voorkomende last

Meest voorkomende belasting is de recht toe recht aan belasting. De vloer is symmetrisch van vorm en dus komt het gewicht ook als rechthoekige belasting op de ligger. De rechtkant bestaat uit het aantal meters dat moet worden meegerekend, vermenigvuldigt met de vierkante meter lasten. Die combinatie wordt dan over de lengte van de ligger als last in rekening gebracht. Dit is de basisvorm van de gelijkmatig verdeelde belasting.

Driehoekslasten

Een variant op de gelijk matig verdeelde belasting is de driehoeksvariant. Daarbij komt een vloer op de ligger aanzetten, echter die vloer heeft een kromme zijde. Oftewel de helft van die kromme zijde dient als last op de balk te worden gezet. Het kan dus schematisch gaan om een rechthoekige belasting met daarop een driehoeksbelasting.

Permanent versus variabel

Belasting dat altijd aanwezig is, valt onder de noemer permanent. Dit wordt gevormd door het eigen gewicht van de ligger of balk. Daarnaast wordt al het rustende gewicht erbij opgeteld. Het gaat om het vloergewicht, afwerking en eventueel dragende wandlasten. Bij variabele belasting daarentegen gaat het om niet altijd aanwezige belasting. Het gaat dus om verkeer van personen of voertuigen. Daarnaast gaat het om inrichting en dingen, welke verplaatst kunnen worden. Daartoe zijn standaard belastingswaarden voor bepaald, welke in kN/m2 worden uitgedrukt. Voor woningen geldt 1,75 kN/m2 terwijl dat voor een kantoorgebouw 2,5 kN/m2 en archief 10,0 kN/m2 bedraagt.

Vertalen belasting naar Q-last

Een stalen ligger voor een opening van 4 m dient 2,5 m aan vloerlasten op te nemen. Daarbij gaat het over 2 m om volledige belasting en over 2 m een driehoekslast. Hoe wordt dan het moment uitgerekend? We gaan uit van een betonvloer van 0,2 m dikte met aanvullende last van 1,2 voor afwerking en lichte wandlasten (0,3 voor eigen gewicht). Daarnaast is een variabele last van 1,75 kN/m2 m van toepassing. Het gaat hierbij om veiligheidsklasse 2, waarvoor binnen de eurocode 1,2 voor permanent en 1,5 voor variabel als veiligheidsklassen gelden:

• q;per;rep = 2,5 * (0,2*24 + 1,2) + 0,3 = 15,3 kN/m;
• q;var;rep = 2,5 * 1,75 = 4,38 kN/m;
• q;per;d = 1,2 * 15,3 = 18,36 kN/m;
• q;var;d = 1,5 * 4,38 = 6,57 kN/m.

Herleiden

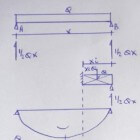
Indien aan de linkerzijde de driehoeksbelasting over de halve lengte aanwezig is en de gelijkmatig verdeelde belasting aan de andere zijde dan geldt:

• totale belasting = 1/4*q*l + 1/2*q*l = 6/24 * q*l + 12/24*q*l = 18/24*q*l;
• ∑M = 0 = 1/3*l * 1/4*q*l + 3/4*l * 1/2*q*l = 1/12*q*l^2 + 3/8*q*l^2 – B*l;
• B = reactiekracht tweede steunpunt = 2/24*q*l + 9/24*q*l = 11/24*q*l;
• A = reactiekracht eerste steunpunt = (18/24-11/24)*q*l = 7/24*q*l;
• x;M;max = 11/24*q*l / q = 11/24*l = de afstand tot het maximale moment naast steunpunt B;
• M;max = 11/24*q*l*11/48*l – 11/24*11/24*q*l^2 = 121/1152*q*l^2-121/576*q*l^2 = -125/1152*q*l^2 (0,1085).

De als driehoek en rechthoek gelijkmatig verdeelde belasting wordt zodoende vertaald naar een maximaal moment.

Bepalen moment

In dit geval vertaalt de belasting naar de volgende momenten:

• M;max;rep = -125/1152*(15,3+4,38)*4^2 = -34,16 kNm;
• M;max;d = -125/1152*(15,3*1,2+4,38*1,5)*4^2 = -43,28 kNm.

Let wel voor geheel geheel gelijkmatig verdeelde belasting (complete vierkant) geldt dat M;max = -1/8*q*l^2 (0,125) en dus is het moment iets groter dan voorgaande voorbeeld.

Lees verder

• Belasting opnamecapaciteit metselwerk, kalkzandsteen, beton
• Overbelasting door sneeuw! Beschouwing materiaal en gewicht
• Onder spanning brengen stalen ligger doorbraak noodzakelijk!