Hoe reken je het weerstandsmoment voor sterkte uit?
Om de sterkte van een balk te kunnen uitrekenen moet worden nagegaan in hoeverre het weerstandsmoment voldoet. Ieder vorm en ieder profiel heeft deze zogeheten W-waarde en is afgeleid van de I-waarde oftewel het traagheidsmoment van de doorsnede. Die waarde wordt gebruikt om de mate van doorbuiging te bepalen, terwijl de W-waarde de feitelijke draagcapaciteit bepaalt (wordt de doorsnede meer belast dan het aan kan zal de constructie feitelijk kapot gaan). Hoe wordt de W-waarde van een doorsnede bepaald en hoe wordt het verder afgeleid?Weerstandsmoment uitrekenen
Weerstandsmoment voor sterkte
Het traagheidsmoment vormt binnen de elastische mechanica een belangrijke eenheid om mee te rekenen, omdat daarmee de doorbuiging van liggers wordt bepaald. De constructie wordt namelijk belast met representatieve belasting en dat leidt tot een vervorming. Daarnaast moet de constructie ook voldoen aan de sterkte, welke wordt gebaseerd op rekenbelasting en het weerstandsmoment. Deze twee worden als volgt berekend:- doorbuiging = δ = Mrep * L^2 / (48 * E * I) met daarin E is elasticiteit en L is de lengte;
- sterkte = σ = Md / Wd ≤ σd;
- I-waarde: is een tot de vierde macht uitkomst dat wordt uitgedrukt in mm^4 als eenheid;
- W-waarde: is een tot de derde macht uitkomst dat wordt uitgedrukt in mm^3.
Rechthoek en vierkant
Bij een rechthoek of vierkant is er sprake van een breedte en een hoogte, waarbij bij de vierkant de maten gelijk aan elkaar zijn. Er is dus sprake van de gekwadrateerde afstand naar het aangrijpingspunt vermenigvuldigd met het oppervlak. Oftewel er is sprake van r^2*dA. Integreren we die beschouwing dan wordt het volgende gevormd:- ∫ r^2*dA waarbij over de hoogte wordt geïntegreerd, wat praktisch inhoudt;
- b*∫ (h)^2*dh = b*1/3*h^3 (over 1/2*y tot -1/2*y) = b/3*[(1/2*h)^3-(-1/2*h)^3] = b/3*[1/8*h^3+1/8*h^3];
- b/3*1/4 *h^3 (b blijft over van het oppervlak, aangezien naar h is geïntegreerd;
- I rechthoek = 1/12 *b*h^3;
- I vierkant = 1/12 *h^4 (b=h).
Om de W-waarde te bepalen dient de zojuist bepaalde waarde te delen door de halve hoogte oftewel:
- W rechthoek = 1/12 *b*h^3 / (1/2*h) = 1/6 * b*h^2;
- W vierkant = 1/6 *h^3.
Driehoek
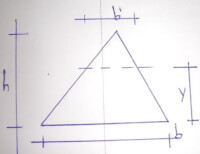Bron: Http://geinformeerd.infoteur.nl- b’ = breedte op hoogte h = b * (1-y/h) waarin y de afstand is tot de basislijn;
- Ip = ∫y^2*dA = ∫y^2*b*(1-y/h)*dy = b*[1/3*y^3-1/4*y^4/h] over 0 tot h = b*[1/3*h^3-1/4*h^3].
Op de basislijn zou gelden:
- Ip driehoek = 1/12 *b*h^3 echter de driehoek dient nog naar het evenwichtspunt worden verplaatst waardoor een correctie op de I waarde volgt van:
- I driehoek = 1/12 *b*h^3 – A*r^2;
- I driehoek = 1/12 *b*h^3 – ½ *b*h*(1/3*h)^2 = 1/12 * b*h^3 – 1/18 *b*h^3 = 1/36 *b*h^3.
Om de W-waarde te bepalen kan worden gebruik gemaakt van de afstand tot de boven en onderkant:
- W driehoek onder = 1/36 *b*h^3 / (1/3*h ) = 1/12 *b*h^2;
- W driehoek boven = 1/36 *b*h^3 / (2/3*h) = 1/24 *b*h^2.
Cirkel en buis
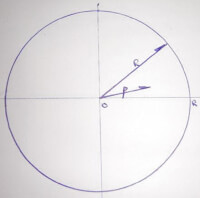Bron: Http://geinformeerd.infoteur.nl- A = oppervlak = π*r^2 = ¼*π*d^2;
- Ip-cirkel = Ix-richting + Iy-richting = ∫ x^2*dA + ∫ y^2*dA = polair traagheidsmoment welke eerst moet worden bepaald;
- Ip = ∫ p^2*dA met dA = 2*π*p*dp met p = de straal over 0 tot r;
- Ip = ∫ p^2*2*π*p*dp = 2*π*[1/4*p^4] over 0 tot r = 2/4*π*r^4 = ½*π*r^4
De polaire I waarde vormt het moment in twee richtingen echter de I-waarde in 1 richting is benodigd, oftewel:
- Ix-cirkel = Iy = [½*π*r^4]/2 = ¼*π*r^4 in geval van een straal;
- Ix-cirkel = 1/64*π*d^4 in geval van een diameter (r^4= (1/2*d)^4= 1/16*d^4);
- Ix-buis = 1/64*π*(D^4-d^4) = ¼*π*(R^4-r^4);
- Wx-cirkel = Wy = Ix of Iy gedeeld door de halve afstand oftewel ½*d of r;
- Wx-cirkel = Wy = ¼*π*r^4 / r = ¼*π*r^3;
- Wx-cirkel = Wy = 1/64*π*d^4/(1/2*d) = 1/32*π*d^3.
- Wx-buis = 1/32*π*(D^4-d^4)/D = ¼*π*(R^4-r^4)/R.
Stelling van Steiner
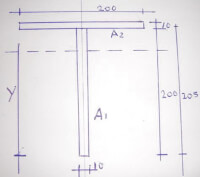Bron: Http://geinformeerd.infoteur.nl- I samengesteld = I1 + A1*(y1-y)^2 + I2 + A2*(y2-y)^2;
- met een totaal oppervlak van A1 + A2;
- y = (A1*yA1 + A2*yA2) / (A1+A2);
- W samengesteld = I samengesteld / y.
Bij een T-balk profiel met lijf is 200 mm hoog, 10 mm dik met een flens daarop van 200 mm breed en 10 mm hoog geldt:
- y = neutrale lijn tot rand = (10*200*100+200*10*205)/(4000) = 152,5 mm;
- I1 = 1/12*10*200^3+200*10*(100-152,5)^2 = 12.179.167 mm^4;
- I2 = 1/12*200*10^3+10*200*(205-152,5)^2 = 5.529.167 mm^4;
- I totaal = 17.708.334 mm^4;
- W samengesteld = 17.708.334/152,5 = 116.120 mm^3.
