Ligging van neutrale lijn samengestelde ligger of oppervlak
Complexe vormen bestaande uit vierkanten, ronde delen, uitstekende strips enzovoorts kunnen een constructief sterke vorm vertegenwoordigen. Samengestelde liggers of aan elkaar gebakken deelvormen vormen een massief geheel, waaraan als geheel constructieve waarden aan toegekend kunnen worden. Denk bijvoorbeeld aan het weerstands- en traagheidsmoment. Voordat het kan worden bepaald, dient van de speciale vorm de ligging van de neutrale lijn te worden bepaald. Hoe reken je uit waar die lijn ligt?Ligging neutrale lijn
Vinden van zwaartepunt tot rand
Iedere vorm heeft een bepaalde afstand tot zijn eigen basis. Denk aan een driehoek, waarbij die lijn ligt op 1/3 van de hoogte. Bij een cirkel is dat uiteraard de straal r en bij een vierkant is het de halve hoogte. Indien er sprake is van een samengestelde constructie dan dient de afstand van iedere afzonderlijke vorm tot de basis van de totale vorm te worden bepaald. Die afstanden zijn gecorreleerd aan het oppervlak van die deelvormen.Vermenigvuldigen afstand met oppervlak
Is het oppervlak mm2 alsmede de afstand y mm van iedere afzonderlijke deelvorm bekend, dan dienen deze waarden te worden vermenigvuldigd. Het vormt het momentane aandeel (kracht x arm of oppervlak x arm) van ieder oppervlak binnen het geheel uitgedrukt in de si-waarde (mm3). Door de afzonderlijke si-waarden van het totaal op te tellen wordt de momentane capaciteit van de complete doorsnede gevonden.Delen door oppervlak
Door de cumulatieve si-waarde van de complete doorsnede te delen door het oppervlak vind je de afstand tot de neutrale lijn. Si / A = mm3/mm2 = mm. De momentane capaciteit van de doorsnede gedeeld door het oppervlak bepaalt dus de resultante van de complete doorsnede. Op die manier kan dus voor iedere samengestelde ligger of vorm de ligging van de neutrale lijn worden bepaald. Hoe reken je het uit volgens twee vorm voorbeelden?T-vormig profiel
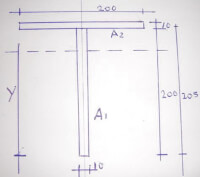Bron: Http://geinformeerd.infoteur.nl- onderste strip = A1 = 10*200 = 2.000 mm2, y1 = 200/2 = 100 mm, s1 = 100*2.000 = 200.000 mm3;
- bovenste strip = A2 = 10*200 = 2.000 mm2, y2 = 200+10/2 = 205 mm, s2 = 205*2.000 = 410.000 mm3;
- si;totaal = 200.000+410.000 = 610.000 mm3;
- oppervlak;totaal = 4.000 mm2;
- afstand neutrale lijn y = 610.000/4.000 = 152,5 mm.
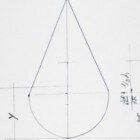
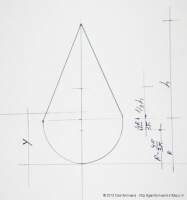
Driehoek op een halve cirkel
Bron: Http://geinformeerd.infoteur.nl- halve cirkel: oppervlak = 1/2*π*r^2, afstand = r - 4*r/(3*π), s1 = r^3*(1/2*π-2/3);
- driehoek: oppervlak = 1/2*(2*r)*h = r*h, afstand = r + 1/3*h, s2 = r^2*h+1/3*r*h^2.
Indien er sprake is van een straal r = 50 en h = 200 dan geldt:
- si;1 = 50^3*(1/2*π-2/3) = 113.016 mm3;
- si;2 = 50^2*200+1/3*50*200^2 = 1.166.667 mm3;
- si;totaal = 113.016+1.166.667 = 1.279.683 mm3;
- oppervlak;totaal = 1/2*π*50^2+50*200 = 13.927 mm2;
- afstand neutrale lijn y = 1.279.683/13.927 = 91,9 mm (op 36,8% van de totale hoogte).
Toepassing binnen mechanica en constructies
Is eenmaal de neutrale lijn van een doorsnede bepaald dan kan daarmee bijvoorbeeld het weerstands- en traagheidsmoment van die doorsnede worden berekend. De stelling van Steiner stelt dat het traagheidsmoment van het totaal wordt bepaald middels het traagheidsmoment van de deelvormen en de kwadratische verplaatsing van die doorsnede naar de neutrale lijn. Oftewel:- I samengesteld = I1 + A1*(y1-y)^2 + I2 + A2*(y2-y)^2 ....
- y = afstand tot neutrale lijn;
- y1, y2 = afstand tot neutrale lijn deelvorm;
- A1, A2 = oppervlak van deelvorm;
- I1, I2 = traagheidsmoment deelvorm (dit is 1/12*b*h^3 voor rechthoeken).
