Wiskunde: continue en discrete kansverdelingen
 Kansrekening is een van de grootste takken van de wiskunde. Het heeft vele praktische toepassingen en wordt dan ook in heel veel situaties gebruikt. Kansverdelingen zijn een van de belangrijkste grondslagen van de kansrekening. Ze vormen de basis voor het uitrekenen van een kans. Er zijn heel veel verschillende kansverdelingen. Sommige verdelingen komen echter vaker voor dan andere. Kansverdelingen kunnen discreet of continu zijn en ze worden allemaal gekenmerkt door eigen verdelingsfuncties.
Kansrekening is een van de grootste takken van de wiskunde. Het heeft vele praktische toepassingen en wordt dan ook in heel veel situaties gebruikt. Kansverdelingen zijn een van de belangrijkste grondslagen van de kansrekening. Ze vormen de basis voor het uitrekenen van een kans. Er zijn heel veel verschillende kansverdelingen. Sommige verdelingen komen echter vaker voor dan andere. Kansverdelingen kunnen discreet of continu zijn en ze worden allemaal gekenmerkt door eigen verdelingsfuncties.
Kansen
Een kans is een maat voor de waarschijnlijkheid dat een gebeurtenis plaatsvindt. Een kans ligt altijd tussen nul en een, of wanneer het in procenten wordt uitgedrukt tussen nul en honderd procent. Een kans kan berekend worden met de zogenaamde distributiefunctie van een kansverdeling. Alle mogelijke gebeurtenissen worden samen de kansruimte genoemd. In 1934 stelde de Russische wiskundige Andrey Kolmogorov de axioma's voor de kansrekening op. Dit waren er drie:- De kans is altijd groter dan nul.
- De kans dat een van de gebeurtenissen uit de kansruimte gebeurt is één.
- De kans op de verenging van onafhankelijke gebeurtenissen uit de kansruimte is gelijk aan de som van de kansen op deze gebeurtenissen.
Discrete kansen
Een kansverdeling is discreet als er eindig, dan wel aftelbaar oneindig gebeurtenissen in de kansruimte zitten. Intuïtief betekent dit dat bij een discrete kans de gebeurtenissen in de kansruimte niet aan elkaar verbonden zijn, maar los van elkaar staan.Continue kansen
Een kansverdeling is continu als er overaftelbaar veel elementen in de kansruimte zitten. Dit betekent dat de kans dat een specifieke waarde precies aangenomen wordt gelijk is aan nul. Dit klinkt raar, maar is te verklaren doordat er oneindig veel waarden aangenomen kunnen worden op een eindig interval. Daarom moet bij continue kansen altijd gekeken worden naar de kans dat de variabele in een bepaald interval ligt. Deze kans is, als er een interval binnen de kansruimte wordt gekozen, altijd groter dan nul.Veelvoorkomende discrete kansverdelingen
De Bernouilliverdeling
De Bernouilliverdeling is de makkelijkste verdeling die er is. Hij wordt gebruikt voor kansexperimenten waarbij er twee mogelijke uitkomsten zijn. Deze worden succes en geen succes genoemd. Er is altijd een zekere kans p op succes, wat automatisch resulteert in een kans van 1-p op geen succes. De Bernouilliverdeling is ook het uitgangspunt voor de binomiale verdeling en de geometrische verdeling.De binomiale verdeling
De binomiale verdeling geeft aan wat de kans is op een bepaald aantal keer succes bij het herhaald doen van onafhankelijke Bernouilli-experimenten. Deze verdeling heeft drie parameters. Deze worden meestal aangeduid met p, n en k. p is net als bij de Bernouilliverdeling de kans op succes. n is het aantal keren dat het experiment wordt herhaald. k is het aantal keren succes. Een binomiale verdeling helpt dus bij het uitrekenen van de kans dat bij n onafhankelijke Bernouilli-experimenten met elk succeskans p, er k keer succes zal zijn.De geometrische verdeling
De geometrische verdeling geeft aan hoe groot de kans is dat we, bij het herhaald uitvoeren van onafhankelijke Bernouilli-experimenten met succeskans p, een bepaald aantal keren moeten wachten tot de eerste keer succes. Deze verdeling heeft dus twee parameters. De succeskans p en het aantal experimenten k. De geometrische verdeling helpt dus bij het uitrekenen van de kans dat we een Bernouilli-experiment met succeskans p, k keer moeten herhalen tot er voor het eerst succes is.De uniforme verdeling
De uniforme verdeling is een verdeling waarbij alle gebeurtenissen in de kansruimte gelijke kans hebben. De kans op een zekere gebeurtenis is dan ook simpelweg één gedeeld door het aantal gebeurtenissen in de kansruimte.De poissonverdeling
De poissonverdeling is een verdeling die aangeeft wat de kans is op een zeker aantal voorvallen in een tijdsinterval, waarbij het gemiddelde aantal voorvallen voor dit tijdsinterval bekend is. Deze verdeling heeft een iets ingewikkeldere opbouw. De distributiefunctie, die aangeeft wat de kans op k voorvallen is, maakt gebruik van de aankomstintensiteit λ (lambda), het aantal voorvallen k en (het getal) e. Het poissonproces is een in de praktijk veelvoorkomend stochastisch proces.Continue kansverdelingen
De uniforme verdeling
De uniforme verdeling heeft ook een continue variant. Omdat de kans op een specifieke waarde altijd nul is moet in dit geval gezegd worden dat de kans dat de waarde in een specifiek interval ligt gelijk is voor alle intervallen van gelijke grootte.De exponentiële verdeling
De exponentiële verdeling is een verdeling die veel voorkomt om de tijd tussen twee gebeurtenissen in te schatten. De verdeling heeft als parameter de intensiteit van de gebeurtenissen, meestal genoteerd als λ. Daarnaast komt ook het getal e voor in de distributiefunctie. Met deze verdeling kan worden berekend hoe groot de kans is dat er een bepaalde tijd gewacht moet worden tussen twee gebeurtenissen.De normale verdeling
De normale verdeling is misschien wel de belangrijkste verdeling die er is. Hij maakt gebruik van een gemiddelde μ (mu) en een standaarddeviatie σ (sigma). Heel veel natuurlijke processen zijn te modelleren als normale verdeeld. Daarnaast is het volgens de centrale limietstelling zo dat een geschaalde optelling van onafhankelijke gelijk verdeelde stochastische variabelen normaal verdeeld is. Ten minste als er genoeg variabelen worden opgeteld. In de statistiek, waar veel gewerkt wordt met steekproeven, is de normale verdeling een heel veel voorkomende verdeling.© 2017 - 2025 Gujanator, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
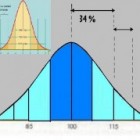 Statistiek de normale verdelingDe functie die voor continue kansvariabelen de kans als functie f van een zekere uitkomst x weergeeft, noemt men de kans…
Statistiek de normale verdelingDe functie die voor continue kansvariabelen de kans als functie f van een zekere uitkomst x weergeeft, noemt men de kans…
 Samenvatting Wiskunde ADit artikel zal als een beknopte samenvatting kunnen worden gelezen voor gevorderden in wiskunde. In dit artikel zal o.a…
Samenvatting Wiskunde ADit artikel zal als een beknopte samenvatting kunnen worden gelezen voor gevorderden in wiskunde. In dit artikel zal o.a…
 Hypergeometrische verdeling: trekkingen zonder terugleggingDe hypergeometrische verdeling is een discrete kansverdeling, waarbij men bij aselecte trekkingen uit de populatie N, me…
Hypergeometrische verdeling: trekkingen zonder terugleggingDe hypergeometrische verdeling is een discrete kansverdeling, waarbij men bij aselecte trekkingen uit de populatie N, me…
 Normaal verdeelde variabelen en waarom ze vaak voorkomenDe normaalverdeling is alomtegenwoordig in de sociale en economische wetenschappen. Het laat een zeer zuinige en dus aan…
Normaal verdeelde variabelen en waarom ze vaak voorkomenDe normaalverdeling is alomtegenwoordig in de sociale en economische wetenschappen. Het laat een zeer zuinige en dus aan…
 Wiskunde: Hoe los je een kwadratische vergelijking op?Kwadratische vergelijkingen komen veel voor in de wiskunde. En niet alleen in de wiskunde. Ze komen eigenlijk voor in al…
Wiskunde: Hoe los je een kwadratische vergelijking op?Kwadratische vergelijkingen komen veel voor in de wiskunde. En niet alleen in de wiskunde. Ze komen eigenlijk voor in al…
 Wiskunde: Het algoritme van KaratsubaVermenigvuldigen is een van de belangrijkste operaties binnen de wiskunde, maar ook binnen vele andere wetenschappen. Ie…
Wiskunde: Het algoritme van KaratsubaVermenigvuldigen is een van de belangrijkste operaties binnen de wiskunde, maar ook binnen vele andere wetenschappen. Ie…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Geralt, Pixabay
- Probability and random processes, Grimmett and Stirzaker
Gujanator (35 artikelen)
Gepubliceerd: 06-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 2
Gepubliceerd: 06-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 2
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.